Kepler Laws Selitys, harjoitukset, kokeilu

Se Kepler -lait Planeettaliikkeestä muotoiltiin saksalainen tähtitieteilijä Johannes Kepler (1571-1630). Kepler päätteli heidät opettajansa Tanskan tähtitieteilijän Tycho Brahen (1546-1601) työn perusteella.

Brahe kokosi huolellisesti planeettaliikkeiden tiedot yli 20 vuoden aikana yllättävän tarkkuuden ja tarkkuuden avulla, jos otetaan huomioon, että kaukoputkea ei ollut vielä keksitty tuolloin,. Tietojesi pätevyys on edelleen voimassa tänään.

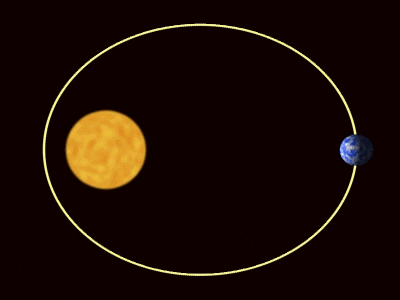Kuvio 1. Planeettojen kiertoradat Keplerin lakien mukaisesti. Lähde: Wikimedia Commons. Willow/CC by (https: // creativecommons.Org/lisenssit/by/3.0)

[TOC]

Keplerin 3 laki

Keplerin lait määräävät:

-Ensimmäinen laki: Kaikki planeetat kuvaavat elliptisiä kiertoratoja auringon kanssa yhdessä valokeilassa.

-Toinen laki tai laki: Linja, joka on suunnattu auringosta mille.

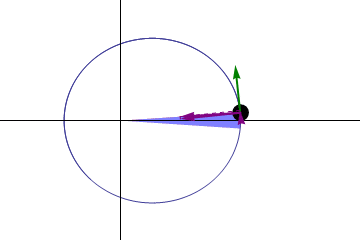Kuva 2. Alueiden laki. Lähde: Wikimedia Commons. Gonfer/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)

-Kolmas laki: Ajan neliö, joka vie minkä tahansa planeetan kiertorata auringon ympäri, on verrannollinen sen keskimääräisen etäisyyden kuutioon aurinkoon.

Olla T sanoi aika, nimeltään Kiertoradan, ja r - Keskimääräinen etäisyys, sitten:

T² on verrannollinen R: hen³

T = k r³

Tämä tarkoittaa, että osamäärä T²/ r³ Se on sama kaikille planeetoille, mikä mahdollistaa kiertoradan säteen laskemisen, jos kiertorata on tiedossa.

Kun T Se ilmaistaan ​​vuosien varrella ja r - Tähtitieteellisissä yksiköissä UA*suhteellisuusvakio on k = 1: n arvoinen:

T²= r³

*Tähtitieteellinen yksikkö vastaa 150 miljoonaa kilometriä, mikä on keskimääräinen etäisyys maan ja auringon välillä. Maan kiertoradan ajanjakso on 1 vuosi.

Universal Gravitation Law ja Keplerin kolmas laki

Universal gravitaatiolaki osoittaa, että kahden massaobjektin välisen gravitaation vetovoiman suuruus M ja m vastaavasti, joiden keskukset ovat erillinen etäisyys r -, Se on annettu:

F = g mm /r²

G on yleinen gravitaatiovakio ja sen arvo on g = 6.674 x 10 ^-yksitoista N.m²/kg² .

Nyt planeettojen kiertoradat ovat elliptisiä hyvin pienellä epäkeskeisyydellä.

Tämä tarkoittaa, että kiertorata ei siirry paljon pois ympyrästä, paitsi joissain tapauksissa, kuten kääpiö Pluto. Jos arvioimme kiertoradat pyöreään muotoon, planeetan liikkeen kiihtyvyys on:

-lla_c = v²/r

Kun otetaan huomioon F = MA, omistaa:

G mm /r² = m.v²/r

Tässä v Se on planeetan lineaarinen nopeus auringon, staattisen ja massan oletuksen ympärillä M, Vaikka planeetta on m. Niin:

Voi palvella sinua: Merkittävät luvut: Säännöt, esimerkit, ratkaisut harjoitukset

Tämä selittää, että aurinkoa kauimpana planeetoilla on pienempi kiertoradan nopeus, koska se riippuu 1/√r.

Koska planeetan kulku etäisyys on suunnilleen kehän pituus: l = 2πr ja se vie yhtä aikaa t, kiertorata, se saadaan:

V = 2πr /t

Molemmat lausekkeet V: lle, joka on voimassa oleva lauseke T: lle, saadaan², Kiertoradan neliö:

Ja tämä on tarkalleen Keplerin kolmas laki, koska tässä ilmaisussa suluissa 4π² /GM Siksi se on vakio, T² on verrannollinen etäisyyteen r - kuutioon korotettu.

Orbitalikauden lopullinen yhtälö saadaan uuttamalla neliöjuuri:

Auringon massan laskeminen

Kuinka paljon auringon massa on? Tämän yhtälön kautta on mahdollista selvittää. Tiedämme, että maan kiertoradan ajanjakso on yksi vuosi ja kiertoradan säde on 1 UA, mikä vastaa 150 miljoonaa kilometriä, joten meillä on kaikki tarvittavat tiedot.

Edellisessä yhtälössämme tyhjentämme M, Mutta ei ennen kuin kaikki arvot muuntaa kansainvälinen yksikköjärjestelmä, jos:

1 vuosi = 3.16 x 10⁷ sekunti.

1 UA = 150 miljoonaa km = 1.5 x10^yksitoista m.

Ja korvaamalla yhtälössä olevat tiedot, saamme melko onnistuneen arvion auringon auringosta 2.0 x 10 ³⁰ kg.

Harjoitukset

Vaikka Keplerillä oli vain planeetat mielessä, kun hän sai kuuluisan laki, nämä ovat päteviä myös satelliittien ja muiden aurinkokunnan elinten liikkeelle, kuten näemme seuraavaksi.

- Harjoitus 1

Tietäen, että Jupiterin kiertorata on 5.19 kertaa suurempi kuin maapallon aika, etsi Jupiterin kiertoradan ajanjakso.

Ratkaisu

Tähtitieteellisen yksikön määritelmän mukaan Jupiter on Sun 5: stä.19 UA, Keplerin kolmannen lain mukaan:

T²= r³= (5,19)³ vuotta

Siksi T = (5,19)^3/2  Vuodet = 11.8 vuotta

- Harjoitus 2

Halley Comet vierailee auringossa 75.3 vuotta. Löytö:

a) sen kiertoradan tärkein puoliksi tukeva.

b) APELIUM -mitta, jos perihelium mittaa 0.568 UA.

Ratkaisu

Halley Comet vierailee auringossa 75.3 vuotta. Löytö:

a) sen kiertoradan tärkein puoliksi tukeva.

b) APELIUM -mitta, jos perihelium mittaa 0.568 UA.

Liittää jhk

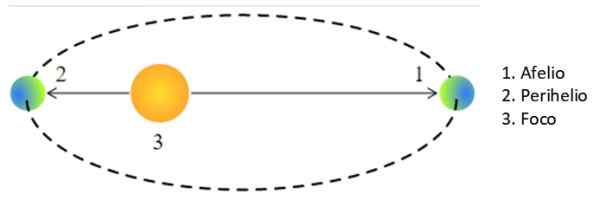
Kun planeetta tai mikä tahansa muu tähti on sen pisteessä lähinnä aurinkoa, sanotaan, että se on perihelio, Ja kun se on kauempana, vuonna aphelion. Pyöreän kiertoradan erityistapauksessa r Keplerin kolmannessa laissa on kiertoradan säde.

Voi palvella sinua: Antoine -vakiot: kaavat, yhtälöt, esimerkit

Elliptisellä kiertoradalla taivaankappale on kuitenkin enemmän tai vähemmän poissa auringosta, koska se on puolimatror “A” Aprotessin ja periheliumin välinen keskiarvo:

Kuva 3. Aflio ja perihelio. Lähde: Wikimedia Commons. Pearson Scott Foresman / Public Domain

Siksi korvaamme R: n Keplerin kolmannessa laissa, joka johtaa Halleylle:

T²= a³→ a = (t)²³ → A = (75.3) ²³ UA = 17.832 UA

Ratkaisu b

A = ½ (perihelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 UA = 35.10 UA.

Koe

Planeettojen liikkumisen analysointi vaatii viikkoja, kuukausia ja jopa vuosia huolellista tarkkailua ja rekisteröintiä. Mutta laboratoriossa voidaan suorittaa hyvin yksinkertainen kokeilu, jotta voidaan todistaa, että Keplerin tasa -arvoinen laki täytetään.

Tätä varten vaaditaan fyysinen järjestelmä, jossa liikettä hallitseva voima on keskeinen, riittävä ehto täytettävien alueiden laki. Tällainen järjestelmä koostuu massasta, joka on sidottu pitkään köyteen, ja kiinteän langan toinen pää tuki.

Taikina erottaa pienen kulman tasapainoasennosta ja tulostetaan lievää impulssia, niin että se suorittaa soikean (melkein elliptisen) liikkeen vaakatasolla, ikään kuin se olisi planeetta auringon ympäri.

Pendulumin kuvaamassa käyrässä voimme todistaa, että se pyyhkäisee yhtä suuret alueet yhtäläisinä aikoina, kyllä:

-Tarkastelemme vektoriradioita vetovoiman keskustasta (alkuperäinen tasapainopiste) massan sijaintiin.

-Ja me barmot kahden peräkkäisen yhtä keston välissä, kahdessa liikkeen eri alueella.

Mitä pidempi heilurilanka ja mitä pienempi kulma, joka poikkeaa pystysuorasta, nettokorjausvoima on vaakasuorempi ja simulaatio muistuttaa liikkeen tapausta keskusvoiman kanssa tasossa.

Sitten kuvattu soikea lähestyy ellipsiä, kuten planeetat matkustavat.

Materiaalit

-Hoitamaton säie

-1 taikina tai metallipallo, joka on maalattu valkoiseksi, joka toimii heilurin linssinä

-Viivotin

-Kuljettaja

-Kuvakamera automaattisella strobe -levyllä

-Tuet

-Kaksi valaistuslähdettä

-Arkki paperia tai mustaa pahvia

Se voi palvella sinua: Big Crunch -teoria: historia, periaatteet, tiedot

Menettely

Kuvan kokoonpano tarvitaan valokuvien ottamiseksi heilurin useista välähdyksistä, kun sen etenemistä seuraa. Tätä varten sinun on laitettava kamera juuri heilurin ja automaattisen strobe -albumin yläpuolelle linssin edessä.

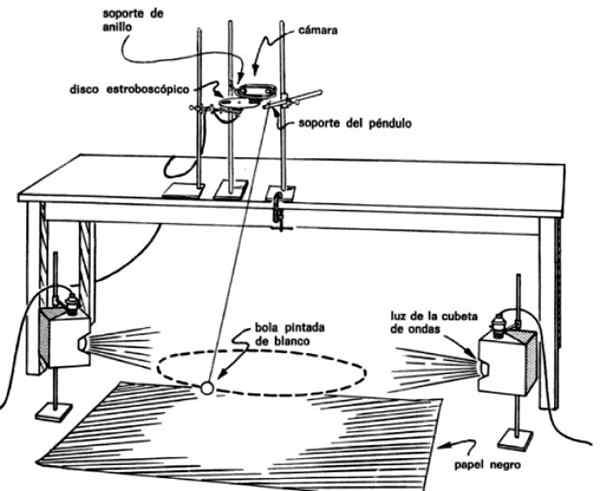Kuva 4. Heilurin kokoonpano varmistaa, että se pyyhkäisee yhtä suuret alueet yhtäläisinä aikoina. Lähde: PSSC -laboratorioopas.

Tällä tavoin kuvat saadaan heilurin säännöllisillä aikaväleillä, esimerkiksi joka 0.1 tai joka 0.2 sekuntia, mikä sallii tietää ajan, joka kului siirtymiseen pisteestä toiseen.

Sinun on myös valaistava heilurin massa kätevästi, asettamalla valot molemmille puolille. Lanssi on maalattu valkoiseksi taustalla olevan kontrastin parantamiseksi, joka koostuu pidennetystä mustasta paperista maassa.

Nyt sinun on tarkistettava, että heiluri pyyhkäisee yhtä suuret alueet yhtäläisinä aikoina. Tätä varten valitaan aikaväli ja heilurin käyttämät pisteet mainitulla aikavälillä on merkitty paperille.

Kuvassa linja piirretään soikean keskustasta näihin pisteisiin, joten meillä on ensimmäinen heiluri pyyhkäisemällä alueet, mikä on suunnilleen elliptinen ala, kuten alla esitetty:

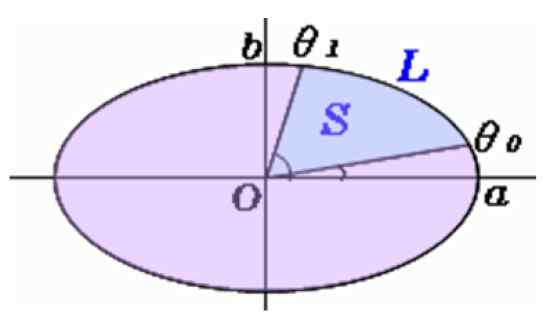Kuva 5. Elliptisen sektorin pinta -ala. Lähde: f. Zapata.

Elliptisen osion alueen laskenta

Kulmat mitataan kuljettimella θ_jompikumpi ja θ₁, Ja tätä kaavaa käytetään S: n löytämiseen, elliptisen sektorin pinta -ala:

S = f (θ₁) - F (θ_jompikumpi-A

Kanssa F (θ) antama:

Ota huomioon, että -lla ja b - Ne ovat puoliksi vastaavasti suurempia ja vähäisiä. Lukijan tulisi huolehtia vain huolellisesti puolijalo- ja kulmien mittaamisesta, koska online -laskimia on helppo arvioida tätä lauseketta.

Jos kuitenkin vaadit laskelman tekemistä käsin, sinun on muistettava, että kulma θ mitataan asteina, mutta tietojen syöttämisen yhteydessä laskuriin on ilmaistava Radianesissa.

Sitten sinun on merkintä toinen pistepari, jossa heiluri on sijoittanut saman aikavälin, ja vedettävä vastaava alue laskemalla sen arvo samalla menettelyllä.

Tasa -arvoisten alueiden lain tarkistaminen

Lopuksi on vielä varmistettava, että alueiden laki on täytetty.

Tulokset poikkeavat hiukan odotetusta? Sinun on pidettävä mielessä, että kaikkiin toimenpiteisiin liittyy heidän vastaava kokeellinen virhe.

Viitteet

1. Keisan -online -laskin. Elliptisen sektorin laskimen pinta -ala. Toipunut: Keisan.Casio.com.
2. Aita. Keplerin planeettaliikkeen laki. Haettu osoitteesta: OpenStax.org.
3. PSSC. Laboratoriofysiikka. Toimitus palautti. Toipunut: Kirjat.Google.yhteistyö.
4. S. S. 2002. Tähtitiede. Schaum -sarja. McGraw Hill.
5. Pérez r. Yksinkertainen järjestelmä keskusvoimalla. Toipunut: Francesphysics.Blogin.com
6. Stern, D. Planeettaliikkeen kolme Kepler -lakia. Palautettu: PHY6.org.