Vektorialgebra

Mikä on vektorialgebra?

Hän Vektorialgebra Se on matematiikan haara, joka vastaa lineaaristen yhtälöiden, vektorien, matriisien, vektoritilojen ja niiden lineaaristen muunnoksien tutkittavien järjestelmien tutkimisesta. Se liittyy muun muassa aluksiin kuin tekniikkaan, differentiaaliyhtälöiden ratkaisu, toiminnallinen analyysi, operaatioiden tutkimus, laskennallinen grafiikka.

Toinen lineaarisen algebran omaksunut alueet on fysiikka, koska tämän kautta on ollut mahdollista kehittää fyysisten ilmiöiden tutkimusta kuvaamalla niitä vektorien käytön kautta. Tämä on mahdollistanut paremman ymmärryksen maailmankaikkeudesta.

Perusteet

Vektorialgebra on peräisin kvaternioiden (reaalilukujen laajentamisen) 1, I, J ja K tutkimisesta sekä Gibbs ja Heaviside edistämä Cartesian geometria, joka huomasi, että vektorit toimivat instrumenttina edustajana useita fyysisiä ilmiöitä.

Vektorialgebraa tutkitaan kolmella säätiöllä:

Geometrisesti

Vektoreita edustavat linjat, joilla on suunta, ja toiminnot, kuten summa, vähentäminen ja kertominen reaalilukulla, määritetään geometrisillä menetelmillä.

Analyyttisesti

Vektorien kuvaus ja niiden toiminta suoritetaan numeroilla, nimeltään komponentit. Tämäntyyppinen kuvaus on geometrisen esityksen tulos, koska koordinaattijärjestelmää käytetään.

Aksiomaattisesti

Vektoreiden kuvaus tehdään koordinaattijärjestelmästä tai minkä tahansa tyyppisestä geometrisesta esityksestä riippumatta.

Avaruuslukujen tutkimus tehdään sen esittämisen kautta vertailujärjestelmässä, joka voi olla yhdessä tai useammassa ulottuvuudessa. Pääjärjestelmien joukossa ovat:

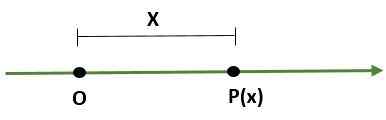
• Yksidimensioinen järjestelmä, että se on viiva, jossa piste (tai) edustaa alkuperää ja toinen piste (p) määrittää asteikon (pituuden) ja tämän suunnan:

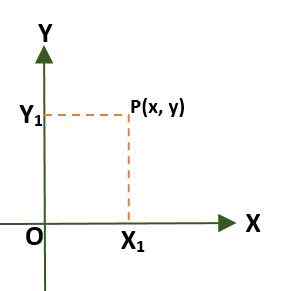
• Suorakulmainen koordinaattijärjestelmä (kaksi dimensionaalista), joka koostuu kahdesta kohtisuorasta viivasta, joita kutsutaan x- ja y -akseliksi, jotka kulkevat pisteen (tai) alkuperän läpi; Tällä tavoin suunnitelma on jaettu neljään alueeseen, joita kutsutaan kvadrantsiksi. Tässä tapauksessa pisteen (p) tasossa annetaan etäisyydet, jotka ovat akselien ja p: n välillä.

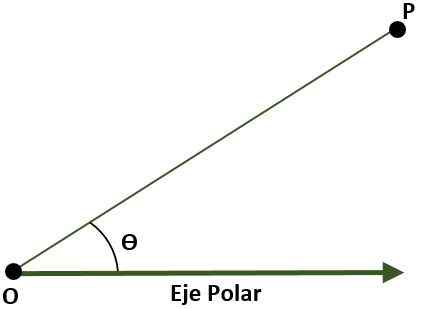
• Polaarinen koordinaattijärjestelmä (Kaksi dimensionaalista). Tässä tapauksessa järjestelmä koostuu pisteestä o (alkuperä), jota kutsutaan napaksi ja puoliksi -reunalla, jolla on alkuperää tai jota kutsutaan polaariseksi akseliksi. Tässä tapauksessa tason pisteen P viitaten napaan ja polaariseen akseliin annetaan kulmalla (ɵ), joka muodostuu lähtö- ja pisteen P välisellä etäisyydellä.

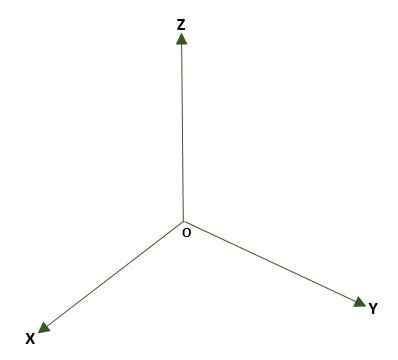
• Suorakaiteen muotoinen kolmiulotteinen järjestelmä, muodostettu kolmella kohtisuoralla viivalla (x, y, z), joiden pisteensä tai avaruus on. Muodostuu kolme koordinaattiasoa: XY, XZ ja YZ; Tila jaetaan kahdeksaan alueeseen, joita kutsutaan oktantiksi. Tilan pisteen P viite annetaan tasoilla ja p: n välillä olevat etäisyydet.

Voimakkuus

Suuruus on fyysinen määrä, joka voidaan laskea tai mitata numeerisella arvolla, kuten joidenkin fysikaalisten ilmiöiden tapauksessa; Näitä ilmiöitä on kuitenkin usein tarpeen kuvata muiden tekijöiden kanssa, jotka eivät ole numeerisia. Siksi suuruudet luokitellaan kahteen tyyppiin:

Skalaarin suuruus

Ne ovat määriä, jotka on määritelty ja edustavat numeerisesti; toisin sanoen moduulilla yhdessä mittayksikön kanssa. Esimerkiksi:

a) Aika: 5 sekuntia.

b) Massa: 10 kg.

c) tilavuus: 40 ml.

d) Lämpötila: 40 ºC.

Vektorin suuruus

Ne ovat niitä määriä, jotka on määritelty ja edustavat moduulia yhdessä yksikön kanssa, samoin kuin mielessä ja suunnassa. Esimerkiksi:

Voi palvella sinua: Ilmaisujen symbolointi

a) Nopeus: (5ȋ - 3ĵ) M/S.

b) Kiihtyvyys: 13 m /s²; S 45º E.

c) Voima: 280 N, 120º.

d) Paino: -40 ĵ kg -f.

Vektorit edustavat vektoreita vektoreita.

Mitkä ovat vektorit?

Vektorit ovat vektorin suuruisia graafisia esityksiä; Eli ne ovat linjasegmenttejä, joissa sen viimeinen pää on nuolen kärki.

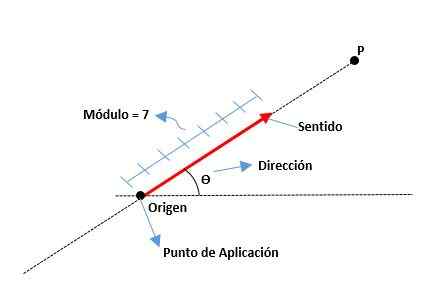
Nämä määritetään sen moduulin tai segmentin pituuden perusteella, sen merkitys, jonka osoittaa nuolen kärki ja sen suunta sen linjan mukaan, johon se kuuluu. Vektorin alkuperä tunnetaan myös sovelluksen pisteeksi.

Vektorin elementit ovat seuraavat:

Moduuli

Se on etäisyys alkuperästä vektorin loppuun, jota edustaa todellinen luku yhdessä yksikön kanssa. Esimerkiksi:

| OM | = | A | = A = 6 cm

Osoite

Käytetään myös X -akselin (positiivisesta) ja vektorin välillä, samoin kuin kardinaalipisteitä (pohjoista, etelää, itää ja länsi) välillä on kulman mitta.

Aisti

Se annetaan vektorin lopussa olevalla nuolen kärkillä, mikä osoittaa, mihin tämä on suunnattu.

Vektorien luokittelu

Yleensä vektorit luokitellaan seuraavasti:

Kiinteä vektori

Se on se, jonka sovelluspiste (alkuperä) on kiinteä; toisin sanoen se pysyy yhteydessä tilaan, joten se ei voi liikkua tässä.

Ilmainen vektori

Se voi liikkua vapaasti avaruudessa, koska sen alkuperä siirtyy mihin tahansa pisteeseen muuttamatta sen moduulia, tarkoittaen tai suuntaa.

Liukuvektori

Se voi siirtää alkuperänsä toimintalinjaan muuttamatta moduuliaan, tarkoittaen tai suuntaa.

Vektoriominaisuudet

Vektoreiden pääominaisuuksista ovat seuraavat:

Varustevektorit

Ne ovat ne vapaat vektorit, joilla on sama moduuli, suunta (tai nämä ovat yhdensuuntaisia) ja järkevät kuin liukuva vektori tai kiinteä vektori.

Vastaavat vektorit

Se tapahtuu, kun kahdella vektorilla on sama osoite (tai ovat samansuuntaiset), sama merkitys, ja huolimatta siitä, että niissä on erilaisia ​​moduuleja ja sovelluspisteitä, ne aiheuttavat yhtäläisiä vaikutuksia.

Vektorin tasa -arvo

Näillä on sama moduuli, suunta ja järki, vaikka niiden lähtökohdat ovat erilaisia, mikä antaa rinnakkaisvektorille siirtyä itseensä vaikuttamatta siihen.

Vastakkaiset vektorit

He ovat niitä, joilla on sama moduuli ja suunta, mutta niiden merkitys on päinvastainen.

Yhtenäinen vektori

Se on yksi, jossa moduuli on yhtä suuri kuin yksikkö (1). Tämä saadaan jakamalla vektori sen moduulilla, ja sitä käytetään vektorin suunnan ja suunnan määrittämiseen joko tasossa tai avaruudessa käyttämällä standardisoituja pohja- tai yksikkövektoreita, jotka ovat:

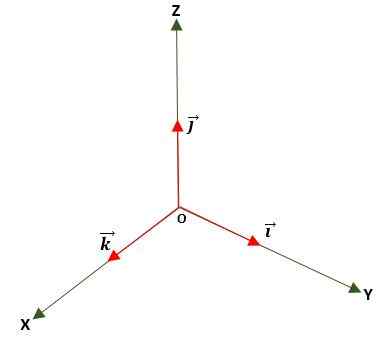
Nollavektori

Se on se, jonka moduuli on yhtä suuri kuin 0; toisin sanoen sen alkuperä- ja äärimmäisyydet ovat samat samat pisteet.

Vektorikomponentit

Vektorin komponentit ovat vektoriprojektioiden arvot vertailujärjestelmän akseleilla; Vektorin hajoamisesta riippuen, joka voi olla kahden tai kolmen ulottuvuuden akseleilla, saadaan kaksi tai kolme komponenttia.

Vektorin komponentit ovat reaalilukuja, jotka voivat olla positiivisia, negatiivisia tai jopa nollaa (0).

Tällä tavoin, jos sinulla on āvektori, joka on peräisin suorakaiteen muotoisesta koordinaattijärjestelmästä XY (kaksi -dimensionaalisessa) tasossa, X -akselin projektio on āx ja Y -akselin projektio ja on āy. Siten vektori ilmaistaan ​​sen komponenttivektoreiden summana.

Esimerkit

Ensimmäinen esimerkki

Sinulla on ā -vektori, joka alkaa sen päiden alkuperästä ja koordinaateista. Siten vektori ā = (ā_x; -Lla_ja) = (4; 5) cm.

Voi palvella sinua: 120 jakajaa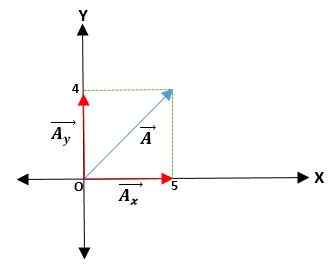

Jos vektori ā toimii kolmen ulottuvuuden kolmionmuotoisen koordinaattijärjestelmän (avaruudessa) x, y, z, toiseen pisteeseen (p), niiden akselien projektiot ovat āx, āy ja āz; Siten vektori ilmaistaan ​​sen kolmen komponenttivektorin summana.

Toinen esimerkki

Sinulla on ā -vektori, joka alkaa sen päiden alkuperästä ja koordinaateista. Siten vektori ā = (a_x; -Lla_ja; -Lla_{z -z}) = (4; 6; -3) cm.

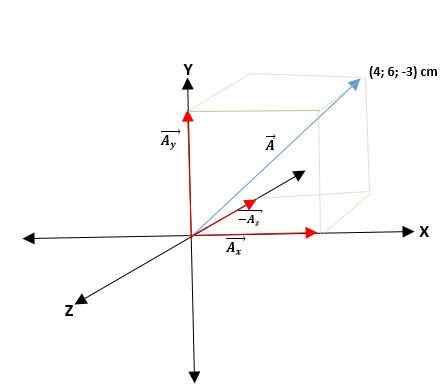
Vektorit, joilla on suorakaiteen muotoiset koordinaatit, voidaan ilmaista heidän perusvektoreidensa mukaan. Tätä varten vain jokainen koordinaatti on kerrottava vastaavalla yksikkövektorilla, jotta tasolle ja tilalle ne ovat seuraavat:

Lentokoneessa: ā = a_xi +a_jaJ -.

Avaruudelle: ā = a_xi +a_jaJ+a_{z -z}k -k -.

Toiminta vektorien kanssa

On olemassa monia suuruuksia, joilla on moduuli, merkitys ja suunta, kuten kiihtyvyys, nopeus, siirtymä, voima, muun muassa.

Niitä sovelletaan eri tieteen aloilla, ja niiden soveltamiseksi on joissakin tapauksissa välttämätöntä suorittaa operaatioita, kuten summa, vähentäminen, kertominen ja vektorien ja skalaarien jakautuminen.

vektorien lisääminen ja vähentäminen

Vektorien summaa ja vähentämistä pidetään yhtenä algebrallisena operaationa, koska vähennys voidaan kirjoittaa summana; Esimerkiksi vektorien ā ja ē vähentäminen voidaan ilmaista seuraavasti:

Ā - ē = ā + (-ē)

Vektorien summan ja vähentämisen suorittamiseksi on olemassa erilaisia ​​menetelmiä: ne voivat olla grafiikkaa tai analytiikkaa.

Graafiset menetelmät

Käytetään, kun vektorilla on moduuli, aisti ja suunta. Tätä varten piirretään viivoja, jotka muodostavat kuvan, joka myöhemmin auttaa määrittämään tuloksena. Tunnetuimpia ovat seuraavat:

Rinnakkaisohjelma

Kahden vektorin summan tai vähentämisen tekemiseksi koordinaatti -akselilla valitaan yhteinen kohta, joka edustaa vektorien alkuperäpistettä -ylläpitäen niiden moduulia, suuntaa ja suuntaa.

Sitten rinnakkaiset viivat vedetään vektoreihin rinnakkaisohjelman muodostamiseksi. Tuloksena oleva vektori on diagonaali, joka lähtee molempien vektoreiden alkuperäpisteestä rinnakkaisogrammin kärkeen:

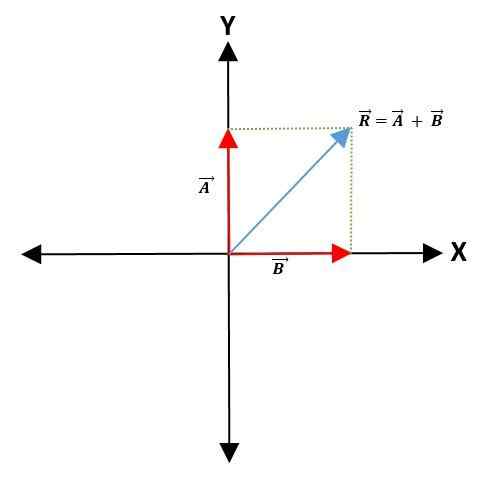
Kolmiomenetelmä

Tässä menetelmässä vektorit sijoitetaan toisen alapuolelle, ylläpitäen niiden moduuleja, aisteja ja osoitteita. Tuloksena oleva vektori on ensimmäisen vektorin alkuperän liitto toisen vektorin lopussa:

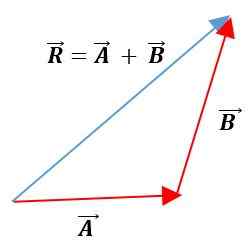
analyyttiset metodit

Kaksi tai useampaa vektoria voidaan lisätä tai vähentää geometrisen tai vektorimenetelmän avulla:

Geometrinen menetelmä

Kun kaksi vektoria muodostavat kolmion tai rinnakkaisogrammin, m [odulo ja tuloksena olevan vektorin suunta voidaan määrittää rinnan ja kosinin lakien avulla. Siten tuloksena oleva vektorimoduuli, joka soveltaa kosinin lakia ja kolmiomenetelmää, annetaan:

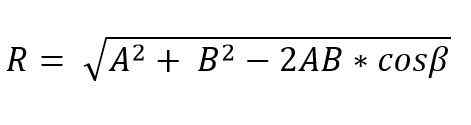
Tässä kaavassa β on vastakkainen kulma kuin R -puolella, ja tämä on yhtä suuri kuin 180º - ɵ.

Toisaalta, rinnakkaisogrammimenetelmällä saatu vektorimoduuli on:

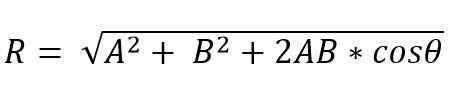
Tuloksena oleva vektoriosoite annetaan kulmalla (α), joka muodostaa tuloksen yhden yhden vektorin kanssa.

Rintalaki, vektorien summa tai vähentäminen voidaan tehdä myös kolmio- tai rinnakkaisohjelmalla, tietäen, että jokaisessa kolmiossa sivut ovat verrannollinen komeiden kulmien rintoihin:

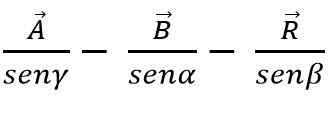
Vektorimenetelmä

Tämä voidaan tehdä kahdella tavalla: sen suorakulmaisista koordinaateista tai sen perusvektoreista riippuen.

Vektorit, jotka tulee lisätä tai vähentää koordinaattien alkuperää kohti ja z); Lopuksi sen komponentit lisätään algebrallisesti. Joten lentokoneelle se on:

Voi palvella sinua: Primo -numerot: Ominaisuudet, esimerkit, harjoitukset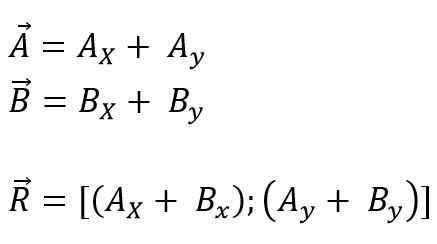

Tuloksena oleva vektorimoduuli on:

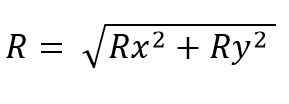
Kun taas avaruudessa se on:

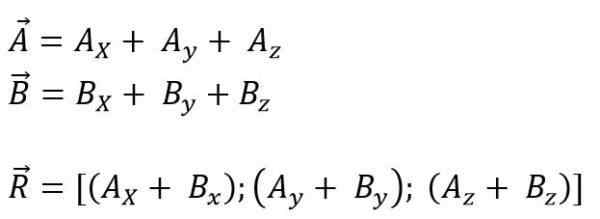
Tuloksena oleva vektorimoduuli on:

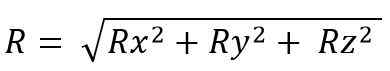
Kun vektorisummia suoritetaan, käytetään useita ominaisuuksia, jotka ovat:

• Assosiatiivinen omaisuus: Tulos ei muutu lisäämällä kaksi vektoria ensin ja lisäämällä sitten kolmas vektori.
• Kommutatiivinen omaisuus: Vektorien järjestys ei muuta tuloksena.
• Vektori jakautuva ominaisuus: Jos skalaari kerrotaan kahden vektorin summalla, se on yhtä suuri kuin skalaarin kertolasku jokaiselle vektorille.
• Jakautuva kiinteistö skalaari: Jos vektori kerrotaan kahden skalaarin summalla, se on yhtä suuri kuin vektorin kertolasku jokaiselle skalaarille.

Vektori kertolasku

Vektoreiden kertolasku tai tuote voitaisiin suorittaa summana tai vähennystä, mutta niin se menettää fyysisen merkityksen ja ei melkein koskaan sovellusten sisällä. Siksi yleensä eniten käytettyjä tuotetyyppejä ovat skalaari- ja vektorituote.

Skalaarituote

Se tunnetaan myös kahden vektorin pisteenä. Kun kaksivektorimoduulia kerrotaan niiden välillä muodostetulla pienellä kulman kosinulla, skalaari saadaan. Kahden vektorin välisen skalaarituotteen ilmaisemiseksi niiden väliin asetetaan piste, ja tämä voidaan määritellä seuraavasti:

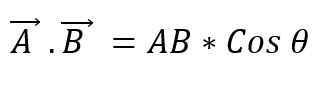
Kahden vektorin välillä olemassa olevan kulman arvo riippuu siitä, ovatko nämä rinnakkaisia ​​vai kohtisuoria; Siten sinun täytyy:

• Jos vektorit ovat yhdensuuntaisia ​​ja niillä on sama merkitys, Coseno 0º = 1.
• Jos vektorit ovat yhdensuuntaisia ​​ja niillä on vastakkaiset aistit, Coseno 180º = -1.
• Jos vektorit ovat kohtisuorassa, Coseno 90º = 0.

Tämä kulma voidaan myös laskea tietäen, että:

Skalaarituotteella on seuraavat ominaisuudet:

• Kommutatiivinen omaisuus: Vektorien järjestys ei muuta skalaaria.
• Jakeluominaisuus: Jos skalaari kerrotaan kahden vektorin summan perusteella, se on yhtä suuri kuin skalaarin kertolasku jokaiselle vektorille.

Vektorituote

Kahden vektorin A ja B vektorikertomus tai ristiintuote johtaa uuteen vektoriin C ja ilmaisee käyttämällä ristiä vektorien keskuudessa:

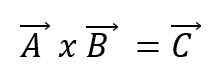
Uudella vektorilla on omat ominaisuutensa. Siten:

• Se osoite: Tämä uusi vektori on kohtisuorassa tasoon nähden, jonka alkuperäiset vektorit määrittelevät.
• Hän aisti: Tämä määritetään oikeanpuoleisella sääntöllä, jossa vektori A käännetään B: hen osoittaen pyörimissuunnan sormilla, ja peukalolla vektorin suunta on merkitty.
• Hän moduuli: Se määritetään AXB -vektorien moduulien kertolaskulla näiden vektoreiden välisen pienen kulman rintaan. Se ilmaistaan:

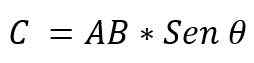
Kahden vektorin välillä esiintyvän kulman arvo riippuu siitä, ovatko nämä rinnakkaisia ​​vai kohtisuoria. Joten on mahdollista vahvistaa seuraava:

• Jos vektorit ovat yhdensuuntaisia ​​ja niillä on sama merkitys, sini 0º = 0.
• Jos vektorit ovat yhdensuuntaisia ​​ja niillä on vastakkaiset aistit, sini 180º = 0.
• Jos vektorit ovat kohtisuorassa, sini 90º = 1.

Kun vektorituote ilmaistaan ​​perusvektoreidensa mukaan, sen on:

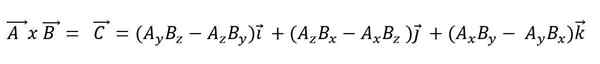
Skalaarituotteella on seuraavat ominaisuudet:

• Se ei ole kommutatiivinen: vektorien järjestys muuttaa skalaaria.
• Jakeluominaisuus: Jos skalaari kerrotaan kahden vektorin summan perusteella, se on yhtä suuri kuin skalaarin kertolasku jokaiselle vektorille.