Vektorin suuruus

Mikä on vektorialue?

Eräs Vektorin suuruus Se on mikä tahansa lauseke, jota edustaa vektori, jolla on numeerinen arvo (moduuli), suunta, suunta ja sovelluspiste. Joitakin esimerkkejä vektorien suuruuksista ovat siirtymä, nopeus, lujuus ja sähkökenttä.

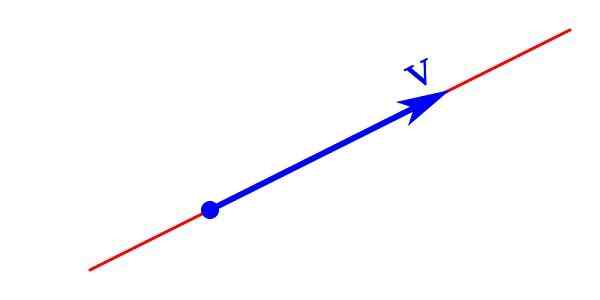
Vektorin suuruuden graafinen esitys koostuu nuolesta, jonka kärki osoittaa sen suunnan ja suunnan, sen pituus on moduuli ja lähtökohta on sovelluspisteen alkuperä tai piste.

Vektorin graafinen esitys

Vektorin suuruus on esitetty analyyttisesti kirjaimella, joka kuljettaa nuolen yläosaan, joka osoittaa oikealle vaakasuunnassa. Sitä voidaan edustaa myös lihavoituna kirjoitetulla kirjeellä V Kenen moduuli ǀVǀ Se on kirjoitettu kursivoituna V.

Yksi vektorin suuruuskonseptin sovelluksista on moottoriteiden ja teiden suunnittelussa, erityisesti sen kaarevien suunnittelussa. Toinen sovellus on siirtymisen laskeminen kahden paikan välillä tai ajoneuvon nopeudenmuutos.

Vektorien elementit

Vektorin suuruus on mikä tahansa yksikkö, jota edustaa linjasegmentti, jonka suunta on avaruudessa, jolla on vektorin ominaisuudet. Sen elementit ovat:

Moduuli: Numeerinen arvo osoittaa vektorin suuruuden koon tai voimakkuuden.

Osoite: Se on linjasegmentin suunta tilaan, joka sisältää sitä. Vektorilla voi olla vaakasuora, pystysuora tai kalteva suunta; Pohjoinen, eteläinen, tämä tai länsi; Koilliseen, kaakkoon, lounaaseen tai luoteeseen.

Aisti: Se on merkitty nuolen kärkeen vektorin lopussa.

Se voi palvella sinua: fysiikkaa ennen kreikkalaisia ​​(Antigua Kreikka)

Sovelluspiste: Se on vektorin alkuperäisen toiminnan alkuperä tai kohta.

Vektoriluokitus

Vektorit luokitellaan kollineaarisiksi, rinnakkaisiksi, kohtisuoriksi, samanaikaisiksi, parisuhteiksi, vapaiksi, liukuviksi, vastakkaisille, laitteille, kiinteiksi ja yksiköksi.

Kolineaali: Ne kuuluvat tai toimivat samalla suoralla linjalla, heitä kutsutaan myös lineaarisesti riippuvainen Ja ne voivat olla pystysuoria, vaakasuoria ja kaltevia.

Rinnakkaisuus: Heillä on sama osoite tai taipumus.

Kohtisuorassa: Kaksi vektoria on kohtisuorassa toisiinsa nähden, kun niiden välinen kulma on 90 °.

Samanaikainen: He ovat vektoreita, jotka liukuvat toimintalinjansa yli, ne osuvat samaan avaruuteen liittyvään vaiheeseen.

Koplanariot: Ne toimivat koneessa, esimerkiksi lentokoneessa Xy.

Vapaa: Ne liikkuvat missä tahansa avaruudessa pitäen moduulinsa, suuntaan ja merkityksen.

Liukua: He liikkuvat heidän suuntaan määritetyn toimintalinjan varrella.

Vastakkaiset: Heillä on sama moduuli ja suunta, ja vastakkainen suunta.

Laitteet: Heillä on sama moduuli, suunta ja merkitys.

Kiinteä: Sovelluksen piste on muuttumaton.

Unakriitit: Vektorit, joiden moduuli on yksikkö.

Vektorikomponentit

Vektorin voimakkuus kolmen dimensionaalisessa tilassa on esitetty kolmen akselin järjestelmässä kohtisuorassa toisiinsa nähden (X ja z) kutsutaan ortogonaaliksi.

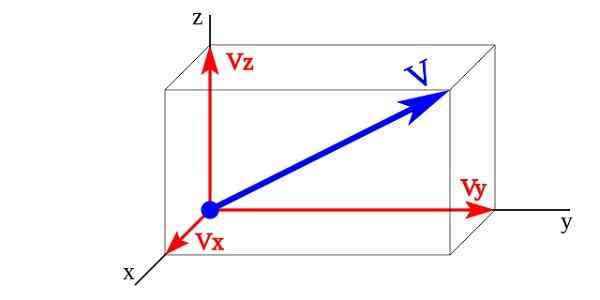Vektorikomponentit, joiden suuruus on

Kuvassa vektorit Vx, Vy, Vz ovat vektorivektorikomponentit V Kenen yksikkövektorit ovat x,ja,z -z. Vektorin suuruus V Sitä edustaa vektorikomponenttien summa.

V = Vx + Vy + Vz

Useiden vektorialueiden tulos on kaikkien vektorien vektorisumma ja korvaa nämä vektorit järjestelmässä.

Vektorikenttä

Vektorikenttä on avaruusalue, jossa jokaisessa pisteessä vektorin suuruus vastaa. Jos ilmenevä suuruus on kehoon tai fyysiseen järjestelmään vaikuttava voima, vektorikenttä on voiman kenttä.

Voi palvella sinua: Steiner Lause: Selitys, sovellukset, harjoitukset

Vektorikenttä esitetään graafisesti kenttäviivoilla, jotka ovat vektorin suuruisten tangenttiviivoja alueen kaikissa kohdissa. Joitakin esimerkkejä vektorikentästä ovat sähkökenttä, joka on luotu nesteen avaruudessa ja nopeuskentällä.

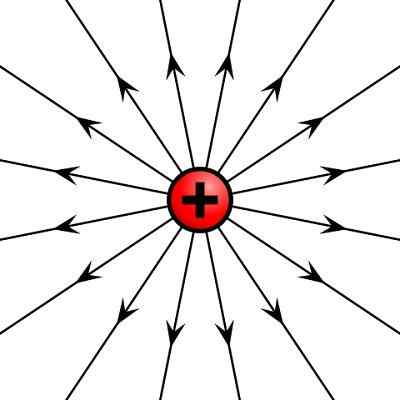Positiivisen sähkövarauksen luominen sähkökenttä

Toiminta vektorien kanssa

Vektorien lisääminen- Se on seurausta kahdesta tai useammasta vektorista. Jos sinulla on kaksi vektoria JOMPIKUMPI ja P Summa on JOMPIKUMPI + P = q. Vektori Q - Tuloksena oleva vektori saadaan graafisesti vektorin alkuperää -Lla vektorin loppuun B -.

Vektorivähennys: Kahden vektorin tai ja ja P On JOMPIKUMPI - P = Q. Vektori Q -  Lisäät vektoriin JOMPIKUMPI Vastapäätä -P. Graafinen menetelmä on sama kuin summa eron kanssa, jonka vastakkainen vektori siirretään äärimmäisyyteen.

Skalaarituote- Skalaarinen tuote -lla vektorin mukaan P Se on vektori Kansanedustaja sillä on sama vektori P. Jos skalaarinen suuruus on nolla, skalaarituote on nollavektori.

Esimerkkejä vektorien suuruuksista

Sijainti

Objektin tai hiukkasen sijainti vertailujärjestelmään on vektori, joka annetaan sen suorakaiteen muotoisilla koordinaateilla X ja z, ja sitä edustaa sen vektorikomponentit Xî, Yĵ, Zk. Vektorit  Yllyttää, ĵ, k -k - He ovat yksikkövektoreita.

Hiukkas yhdessä vaiheessa (X ja z) on sijaintivektori r - = Xî + Yĵ + Zk. Vektoriaseman numeerinen arvo on r -= √ (x² + ja² + z -z²-A. Hiukkasten sijainnin muutos asemasta toiseen vertailujärjestelmän suhteen on vektori Siirtymä ΔR Ja se lasketaan seuraavalla vektorilaatikolla:

Voi palvella sinua: Anodiset säteet

ΔR = r₂ - r -₁

Kiihtyvyys

Keskimääräinen kiihtyvyys (-lla_m) Se määritellään nopeuden vaihteluna v Aikavälillä Δt Ja lauseke sen laskemiseksi on -lla_m= Δv/Δt, olemus ΔV Vektorimuutosnopeus.

Välitön kiihtyvyys (-lla) on keskimääräisen kiihtyvyyden raja -lla_m kun Δt muuttuu niin pieneksi, että sillä on taipumus nolla. Välitön kiihtyvyys ilmaistaan ​​sen vektorikomponenttien mukaan

-lla =-lla_xYllyttää +-lla_ja ĵ+ -lla_{z -z}k -k -

Gravitaatiokenttä

Massan aiheuttama painovoima vetovoima M, Sijaitsee alkuperässä, toisella massalla m Yhdessä avaruudessa x, ja, z -z Se on vektorikenttä, nimeltään Gravitational Force -kenttä. Tämä voima annetaan ilmaisulla:

F= (-mmg/r --Aȓ

r - = Xî + Yĵ + Zk

F = Se on fyysisen voimakkuuden painovoima

G = on yleinen gravitaatiovakio

ȓ = on massa -aseman vektori m

Viitteet

1. Tallack, J C. Johdanto vektorianalyysiin. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S ja Spellman, D. Analyysivektori. s.lens. : MC Graw Hill, 2009.
3. Brändi, l. Analyysivektori. New York: Dover Publications, 2006.
4. Griffiths, D J. Johdanto elektodynaamioon. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Haag, b. Johdatus vektorianalyysiin. Glasgow: Methuen & Co. Ltd, 2012.