Painotettu keskiarvo, miten se lasketaan, esimerkkejä ja harjoituksia

Se Painotettu keskiarvo tai painotettu aritmeettinen keskiarvo, se on keskeinen taipumusmitta, jossa jokaiselle x -arvolle_Yllyttää joka voi ottaa muuttujan x, peso p on määritetty_Yllyttää. Seurauksena on merkitsemällä painotettu keskiarvo x_p, Sinulla on:

Summan summan myötä painotetun keskiarvon kaava on:

Missä N edustaa muuttujan x valittujen arvojen määrää.

P_Yllyttää, jota kutsutaan myös painokerroin, Se on mitta siitä, kuinka tärkeä tutkija määrittelee jokaiselle arvolle. Tämä tekijä on mielivaltainen ja aina positiivinen.

Tässä, että painotettu keskiarvo eroaa yksinkertaisesta aritmeettisesta keskiarvosta, koska tässä jokainen arvo x_n Sillä on yhtä merkitys. Useissa sovelluksissa tutkija kuitenkin mahdollisesti katsoo, että jotkut arvot ovat tärkeämpiä kuin toiset ja antavat painon niiden kriteerien mukaisesti.

Tässä on tunnetuin esimerkki: Oletetaan, että opiskelija esittelee n arvioita yhdessä aiheessa ja kaikilla on sama paino viimeisessä nuotissa. Tässä tapauksessa lopullisen huomautuksen laskemiseksi se riittää yksinkertaisen keskiarvon tekemiseen, ts. Lisää kaikki pätevyydet ja jakaa tulos n: llä.

Mutta jos jokaisella toiminnalla on erilainen paino, koska jotkut arvioivat tärkeämpää tai monimutkaisempaa sisältöä, niin on tarpeen kertoa jokainen arviointi vastaavalla painolla ja lisätä sitten tulokset lopullisen luokituksen saamiseksi. Näemme, kuinka tämä menettely toteutetaan ratkaistuissa harjoitusosassa.

[TOC]

Esimerkit

Kuvio 1. Painotettua keskiarvoa käytetään kuluttajahintaindeksin laskettaessa, inflaatioindikaattori. Lähde: Pxhere.

Edellä kuvattujen tutkintojen esimerkki on yksi tyypillisimmistä painotetun keskiarvon soveltamisen suhteen. Toinen erittäin tärkeä sovellus taloudessa on kuluttajahintaindeksi jompikumpi Kuluttajan hintaindeksi IPC, jota kutsutaan myös perhekori ja se toimii inflaation arvioijina taloudessa.

Voi palvella sinua: kulmat ja kolmiot

Suunnittelussaan otetaan huomioon sarja esineitä, kuten elintarvike- ja alkoholittomia juomia, vaatteita ja jalkineita, lääkkeitä, liikennettä, viestintää, koulutusta, vapaa -aikaa ja muita tavaroita ja palveluita.

Asiantuntijat osoittavat jokaiselle kentälle painotuskerroksen niiden merkityksen mukaan ihmisten elämässä. Hinnat kerätään vakiintuneeksi ajanjaksolle, ja kaikilla tiedoilla, jotka on laskettu mainittuja ajanjaksoon, joka voi olla kuukausittain, kahden hengen puolivuosittain tai vuosittain, esimerkiksi.

Hiukkasjärjestelmän massakeskus

Fysiikassa painotetulla keskiarvolla on tärkeä sovellus, joka on laskea Massakeskus hiukkasjärjestelmä. Tämä käsite on erittäin hyödyllinen työskennellessään laajennetun kehon kanssa, jossa sen geometria tulisi ottaa huomioon.

Massikeskus määritellään pisteeksi, jossa laajennetun esineen koko massa on keskittynyt. Tässä vaiheessa voimia voidaan levittää esimerkiksi painona, ja siten selittää niiden käännös- ja kiertoliikkeet samojen tekniikoiden kautta, joiden kanssa ne toimivat, kun kaikkien esineiden piti olla hiukkasia.

Yksinkertaisuuden mukaan se alkaa olettaa, että laajennettu runko koostuu määrästä N hiukkasia, kukin niistä massalla m ja sen oma sijainti avaruudessa: koordinaattipiste (x_Yllyttää, ja_Yllyttää, z -z_Yllyttää-A.

Olla x_Cm Koordinaatti x CM: n keskustasta, sitten:

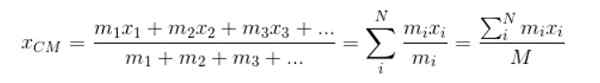
M edustaa järjestelmän kokonaismassaa. Etenee samalla tavalla löytää koordinaatit ja_Cm ja z_Cm-

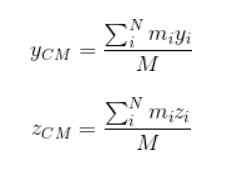
Painotuskerroin tässä tapauksessa on kunkin pidennetyn esineen muodostavan hiukkasen massa.

Voi palvella sinua: Transsendenttiset toiminnot: Tyypit, määritelmä, ominaisuudet, esimerkit

Massikeskuksen tärkeät ominaisuudet

Kun hiukkasten lukumäärä on erittäin suuri, se on jatkuva esine. Tässä tapauksessa n → ∞ ja summa korvataan määritellyllä integraalilla, jonka rajat annetaan objektin koon avulla.

On tärkeää korostaa se, että massakeskuksen sijainnissa ei välttämättä ole massaa. Esimerkiksi Donits -munkissa massakeskus osuu enemmän tai vähemmän rosquillan geometriseen keskukseen.

Kuva 2. Donitsin massakeskus, melko symmetrinen esine, on reiässä. Lähde: Pixabay.

Massikeskuksen sijainti ei riipu hiukkasten sijaintien määrittämisestä, koska se on ominaisuus, joka riippuu itse objektin kokoonpanosta eikä siitä, miten se näkyy erilaisista vertailukehyksistä.

Ratkaisut

- Harjoitus 1

Monissa tapauksissa opettajat antavat erilaisia ​​painoja tai prosenttimääriä jokaiselle tuolin arviointitoiminnalle. Siten esimerkiksi tehtävissä on prosenttiosuus, muut eri kokeet ja vuoden loppukokeet yksi todennäköisesti paljon suurempi.

Kuva 3. Arviointisuunnitelmissaan opettajat määräävät yleensä erilaisia ​​painoja arvioinnille. Lähde: David Mulderin luokkakirja Flickrin kautta.

Oletetaan, että tietyssä aiheessa arviointitoimet ja niiden painot ovat seuraavat:

-Talon tehtävät: 20 %

-Lyhyet kokeet: 25 %

-Laboratorioraportit: 25 %

-Loppukoe: 30 %

a) Kuinka opettaja laskee tämän aiheen lopullisen luokan jokaiselle opiskelijalle?

b) Oletetaan, että tietyn opiskelijan pätevyydet ovat asteikolla 1-5 seuraavat:

-Tehtävät: 5.0 pistettä

-Lyhyet kokeet: 4.7 pistettä

-Laboratorioraportit: 4.2 pistettä

-Loppukoe: 3.5 pistettä

Se voi palvella sinua: Enegon: Ominaisuudet, miten tehdä enegon, esimerkkejä

Löydä oppilaan viimeinen huomautus tästä aiheesta.

Ratkaisu

a) Jokaisella arvioinnilla on erilainen paino, jonka opettaja on osoittanut monimutkaisuuden ja omien kriteeriensä mukaan. Tällä tavoin lopullinen luokitus lasketaan suoraan seuraavasti:

Lopullinen = (x20 % tehtävät + lyhyet kokeet x25 % + raportit x25 % + loppukoe x30 %) / 100

b) lopullinen = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) pisteet = 4.275 pistettä ≈ 4.3 pistettä

- Harjoitus 2

Vaatemyymälän omistajat ostivat farkut kolmelta eri toimittajalta.

Ensimmäiset myivät 12 yksikköä hintaan 15 euroa, toinen 20 yksikköä klo 12.80 € ja kolmasosa osti paljon 80 yksiköltä 11 -vuotiaana.50 €.

Mikä on kaupan omistajien maksamat keskimäärin jokaisesta cowboyista?

Ratkaisu

x_p = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 €

Kunkin cowboyn arvo on 12.11 €, riippumatta siitä, että jotkut maksavat vähän enemmän ja toiset hieman vähemmän. Olisi ollut täsmälleen sama, jos myymälän omistajat olisivat ostaneet 112 farkkua yhdeltä toimittajalta, joka olisi myynyt ne 12.11 € pala.

Viitteet

1. Arvelo, a. Keskeisen taipumuksen mittaukset. Haettu: Franarvelo.WordPress.com
2. Mendenhall, W. 1981. Hallinnon ja taloustieteen tilastot. Kolmas. painos. Iberoamerica -toimitusryhmä.
3. Moore, D. 2005. Perustilastot. Toinen. Painos.
4. Triola, m. 2012. Perustilastot. 11. päivä. Ed. Pearson -koulutus.
5. Wikipedia. Painotettu keskiarvo. Haettu: vuonna.Wikipedia.org