Sijaintitoimenpiteet, keskeinen taipumus ja leviäminen

Se Keski-, hajonta- ja aseman taipumuksen mittaukset, Nämä ovat arvoja, joita käytetään tulkitsemaan joukko tilastotietoa. Niitä voidaan työskennellä suoraan, kuten tilastollisesta tutkimuksesta saadaan tai ne voidaan järjestää saman taajuuden ryhmissä, mikä helpottaa analyysiä.

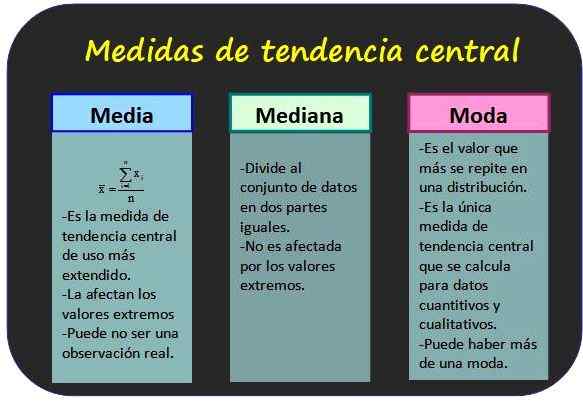
Kolme tunnetuinta keskeistä trenditoimenpiteitä ja joitain sen ominaisuuksia. Lähde: f. Zapata.

Keskeisen taipumuksen mittaukset

Ne sallivat tietää, mitkä arvot tilastotiedot on ryhmitelty yhteen.

Aritmeettinen keskiarvo

Se tunnetaan myös muuttujan arvojen keskiarvona ja saadaan lisäämällä kaikki arvot ja jakamalla tulos tietojen kokonaismäärällä.

• Aritmeettinen keskiarvo tietojen suhteen ilman ryhmittelyä

Ole X -muuttuja, josta ei ole tietoa järjestämättä tai ryhmittelemättä, sen aritmeettinen keskiarvo lasketaan seuraavasti:

Ja yhteenvetomerkinnässä:

Esimerkki

Vuoristomatkailahostellin omistajat aikovat tietää kuinka monta päivää keskimäärin vierailijoita jää tiloihin. Tätä varten suoritettiin tietue 20 turistiryhmän pysyvyydestä, jolloin saatiin seuraavat tiedot:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Keskimääräiset päivät, jolloin turistit oleskelevat, on:

= 2.5 päivää

• Aritmeettinen keskiarvo ryhmiteltyjen tietojen suhteen

Jos muuttujadata on järjestetty absoluuttisessa taajuustaulussa F_Yllyttää Ja luokkakeskukset ovat x₁, x₂,…, X_n, Keskimäärin lasketaan:

Kesän summaus:

Mediaani

Muuttujan X N -arvojen mediaani on ryhmän keskeinen arvo, edellyttäen, että arvot järjestetään yhä enemmän. Tällä tavoin puolet kaikista arvoista on alhaisempia kuin muoti ja toinen puoli on suurempi.

• Ryhmää koskevan tiedon väliaine

Seuraavat tapaukset voidaan esittää:

-Muuttujan x luku N -arvot  outo: Mediaani on arvo, joka on vain arvoryhmän keskellä:

-Muuttujan x luku N -arvot pari: Tässä tapauksessa mediaani lasketaan dataryhmän kahden keskusarvoksi:

Esimerkki

Löydät turisti -hostellitietojen mediaanin, ne on ensin tilattu vähiten suurimmaksi:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Se voi palvella sinua: mikä on suhteellinen taajuus ja miten se lasketaan?

Tiedonumero on tasainen, siksi on olemassa kaksi keskeistä tietoa: x₁₀ ja x_yksitoista Ja koska molemmat ovat 2 arvoisia, myös sen keskimäärin.

Mediaani = 2

• Ryhmiteltyjen tietojen väliaine

Käytetään seuraavaa kaavaa:

Kaavan symbolit tarkoittavat:

-C: Intervallileveys, joka sisältää mediaania

-B -_M: saman aikavälin alaraja

-F_m: havaintojen lukumäärä, jotka sisältävät välin, johon mediaani kuuluu.

-N: Kokonaistiedot.

-F_Bm: havaintojen lukumäärä ennen mediaania sisältävää aikaväliä.

Muoti

Ryhmää koskevan datan muot. Sitä pidetään muotilla edustavimpana tietona tai jakeluluokkaana.

Tämän toimenpiteen kaksi tärkeätä ominaisuutta on, että tietojoukolla voi olla useampi kuin yksi muoti, ja muoti voidaan määrittää sekä kvantitatiiviselle että laadulliselle tiedoille.

Esimerkki

Turisti -hostellin tietojen jatkaminen, joka toistetaan eniten on 1, siksi tavallisin asia on, että turistit pysyvät yhden päivän hostellissa.

Dispersion mitat

Dispersiotoimenpiteet kuvaavat, kuinka ryhmitelty tieto keskusmittarien ympärille on.

Etäisyys

Se lasketaan vähentämällä tärkeimmät tiedot ja pienet tiedot. Jos tämä ero on suuri, se on merkki siitä, että tiedot ovat hajaantuneita, kun taas pienet arvot osoittavat, että tiedot ovat lähellä keskiarvoa.

Esimerkki

Turisti -hostellitietojen alue on:

Alue = 5−1 = 4

Varianssi

• Ryhmittelemättömän tiedon variaatio

Varianssin S² Aritmeettinen keskiarvo on välttämätöntä ensin tietää, sitten ero lasketaan neliöön kunkin datan ja keskiarvon välillä, kaikki lisätään ja jaetaan kokonaishavainnoilla. Nämä erot tunnetaan nimellä poikkeamat.

Varianssi, joka on aina positiivinen (tai nolla), osoittaa, kuinka pitkälle keskiarvon havainnot ovat: Jos varianssi on korkea, arvot ovat hajaantuneempia kuin silloin, kun varianssi on pieni.

Esimerkki

Matkailuhostellin tietojen varianssi on:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Varianssi ryhmiteltyihin tietoihin

Ryhmittelemän tiedon ryhmän varianssin löytämiseksi ne vaaditaan: i) keskiarvo, ii) taajuus f_Yllyttää  joka on kunkin luokan kokonaistiedot ja iii) x_Yllyttää  tai luokan arvo:

Se voi palvella sinua: kolmiotyypit

Keskihajonta

Vakiopoikkeama on varianssin positiivinen neliöjuuri, joten sillä on etu varianssiin nähden: se tulee samoihin yksiköihin kuin tutkittavalla muuttujalla, ja siten on suorempi idea kuin lähellä tai kaukana, joka on keskiarvon muuttuja.

• Vakiopoikkeama ryhmittelemättömille tiedoille

Se määritetään yksinkertaisesti etsimällä vertaansa vailla olevan tiedon varianssin neliöjuuri:

 Esimerkki

Turisti -hostellitietojen keskihajonta on:

S = √ (s²) = √1.95 = 1.40

• Ryhmitetyn datan keskihajonta

Se lasketaan etsimällä ryhmitetyn datan varianssin neliöjuuri:

Sijaintitoimenpiteet

Paikkatoimenpiteet jakavat järjestetyn tietojoukon yhtä suuriksi osiin. Mediaani, sen lisäksi, että keskeinen taipumusmitta on myös sijainti, koska se jakaa kokonaisuuden kahteen yhtä suureen osaan. Mutta voit hankkia pienempiä osia kvarteilla, desileillä ja prosenttipisteillä.

Kvartiilit

Kvartiilit jakavat asetettu neljään yhtä suureen osaan, jokaisella on 25 % tiedoista. Ne merkitään nimellä Q₁, Q -₂ ja Q₃ Ja mediaani on kvartiili Q₂. Tällä tavoin 25% tiedoista on alle kvartiilin q₁, 50% alle kvartiilin q₂ tai mediaani ja 75% kvartiilin q alla₃.

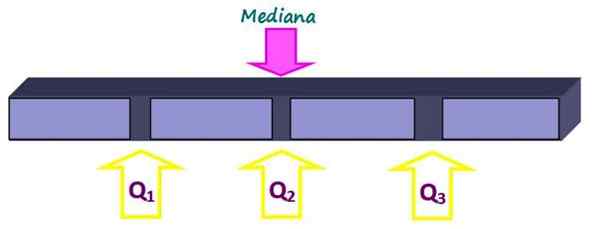Kuva 2. Kvartiilit jakavat tietojoukot neljään yhtä suureen osaan. Lähde: f. Zapata.

• Ryhmää koskevat kvartiilit

Tiedot tilataan ja kokonaismäärä jaetaan 4 ryhmään, joilla on sama määrä tietoja. Ensimmäisen kvartiilin sijainti löytyy:

Q -₁ = (n+1)/4

Ovat kokonaistiedot. Jos tulos on koko kyseistä sijaintia vastaava tieto.

Esimerkki

Ensimmäisen kvartiilin q sijainti₁ Turistikastellin tiedot ovat:

Q -₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Tämä on kvartiilin 1 sijainti ja koska tulos on desimaalin tarkkuudella, data x -tiedot haetaan₅ ja x_6, jotka ovat vastaavasti x₅ = 1 ja x₆ = 1 ja ne on keskiarvo, tuloksena:

Ensimmäinen kvartiili = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Toisen kvartiilin q sijainti₂ On:

Voi palvella sinua: Teleskooppinen summa: Kuinka se on ratkaistu ja ratkaistu harjoitus

Q -₂ = 2 (n+1)/4 = 10.5

Mikä on keskimäärin x: n välillä₁₀ ja x_yksitoista ja tapahtuu samanaikaisesti mediaanin kanssa:

Toinen kvartiili = mediaani = 2

Kolmas kvartiilin sijainti lasketaan:

Q -₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Se on myös desimaalia, joten x on keskiarvo_viisitoista ja x₁₆-

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Mutta koska molemmat ovat 4: n arvoisia:

Kolmas kvartiili = 4

Yleinen kaava kvartiilien sijainnille vertaansa vailla tiedossa on:

Q -_{k -k -} = K (n+1)/4

K = 1,2,3: n kanssa.

• Kvartiilit ryhmiteltyihin tietoihin

Ne lasketaan samanlaisina kuin mediaani:

Symbolien selitys on:

-B -_{Q -}: kvartiilin sisältävän aikavälin alaraja

-C: Tämän ajanjakson leveys

-F_{Q -}: Havaintojen lukumäärä sisälsi kvartiilivälin.

-N: Kokonaistiedot.

-F_Bq: tietojen lukumäärä ennen kvartiiliä sisältävää aikaväliä.

Desilit ja prosenttipisteet

Desilit ja prosenttipisteet jakavat tietojoukon 10 yhtä suureen osaan ja 100 yhtä suurta osaa, ja niiden laskenta suoritetaan analogisesti kvartiilien kanssa.

• Ryhmätietojen desilit ja prosenttipisteet

Kaavoja käytetään vastaavasti:

D -d_{k -k -} = K (n+1)/10

K = 1,2,3… 9.

Desili d₅ Sen on oltava yhtä suuri kuin mediaani.

P_{k -k -} = K (n+1)/100

K = 1,2,3… 99.

Prosenttipiste p_{viisikymmentä} Sen on oltava yhtä suuri kuin mediaani.

Esimerkki

Turisti -hostellin esimerkissä D: n sijainti₃ On:

D -d₃ = 3 (20+1)/10 = 6.3

Kuinka desimaalin lukumäärä on keskimäärin x₆ ja x_7, molemmat yhtä suuri kuin 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Tarkoittaa, että 3 kymmenesosaa tiedosta on alle x₇ = 1 ja jäljellä oleva yllä.

• Ryhmitetyn tiedon desilit ja prosenttipisteet

Kaavat ovat analogisia kvartiilien kanssa. D: tä käytetään desilien ja p: n merkitsemiseen prosenttipisteissä ja symbolit tulkitaan samalla tavalla:

Empiirinen sääntö

Kun tiedot jakautuvat symmetrisesti ja jakauma on yksimodaalinen, on sääntö, jota kutsutaan  Empiirinen sääntö jompikumpi Sääntö 68 - 95 - 99, Se ryhmittelee heidät seuraavilla aikaväleillä:

• 68% tiedoista on aikavälillä:

• 95% tiedoista on aikavälillä:

• 99% tiedoista on aikavälillä:

Esimerkki

Missä aikavälillä on 95% turisti -hostellitiedoista?

Ne ovat aikavälillä: [2.5–1.40; 2.5+1.40] = [1.1; 3.9].

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
4. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.