Määrityskertoimen kaavat, laskenta, tulkinta, esimerkit

Hän Määrityskerroin Se on välillä 0 ja 1, joka edustaa pisteiden (x, y) osuutta, jotka seuraavat säätöviivaa tietojoukon regressiolla kahdella muuttujalla.

Se tunnetaan myös nimellä hyvyyden säätäminen ja sitä merkitään r². Sen laskemiseksi osamäärä on otettu regressiomallin arvioiden ŷi -tietojen ja kunkin datan XI: n vastaavien YI -tietojen varianssin välillä.

R -² = Sŷ / sy

Kuvio 1. Korrelaatiokerroin neljälle dataparille. Lähde: f. Zapata.

Jos 100% tiedoista on regressiofunktioviivalla, määrityskerroin on 1.

Päinvastoin, jos tietojoukolle ja tietylle säätötoiminnolle R -kerroin r² Se osoittautuu yhtä suureksi kuin 0.5, sitten voidaan sanoa, että säätö on tyydyttävä tai hyvä 50 prosentilla. 

Samoin kun regressiomalli heittää R: n arvot² Alle 0.5, tämä osoittaa, että valittu säätöfunktio ei sovi tyydyttävästi tietoihin, joten se on tarpeen toisen säätötoiminnon etsimiseksi.

Ja milloin kovarianssi tai korrelaatiokerroin Sillä on taipumus nolla, silloin muuttujat x ja y tiedoista eivät liity toisiinsa, ja siksi r² on myös taipumus nolla.

[TOC]

Kuinka laskea määrityskerroin?

Edellisessä osassa sanottiin, että määrityskerroin lasketaan etsimällä varianssien välinen osoitus:

-Arvioidaan muuttujan regressiofunktiolla ja 

-Yi -muuttuja, joka vastaa kutakin XI -muuttujaa. 

Matemaattisessa muodossa se pysyy näin:

R -² = Sŷ / sy

Tästä kaavasta seuraa, että r² edustaa regressiomallilla selitettyä varianssia. Vaihtoehtoisesti R voidaan laskea² Seuraavan kaavan kautta, täysin vastaava edellistä:

R -² = 1 - (Sε / SY)

Missä Sε edustaa jätteen varianssia εi = ŷi - yi, kun taas SY on tietojen tietojoukon varianssi. ŶI: n määrittämiseksi regressiofunktiota sovelletaan, mikä tarkoittaa, että ŷi = f (xi).

Se voi palvella sinua: fraktio vastaa 3/5 (ratkaisu ja selitys)

Yi -tietojoukon varianssi, I: stä 1: stä N: ään lasketaan tällä tavalla:

SY = [σ (yi -)² ) / (N-1)]

Ja jatka sitten samalla tavalla Sŷ: lle tai Sε: lle.

Havainnollistava tapaus

Osoittamalla yksityiskohdat tavasta, jolla laskenta Määrityskerroin Otamme seuraavan neljän tietoparin: 

(X, y): (1, 1); (23); (3, 6) ja (4, 7).

Tälle tietojoukolle ehdotetaan lineaarista regression säätöä neliön vähimmäismenetelmällä:

f (x) = 2.1 x - 1 

Tätä säätötoimintoa sovelletaan vertaiskäyttäjät:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) ja (4, 7.4).

Sitten lasketaan aritmeettinen keskiarvo x: lle ja y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Varianssi SY

SY = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Varianssi Sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Määrityskerroin r²

R -² = Sŷ / sy = 7.35/7.58 = 0.97

Tulkinta

Edellisessä segmentissä tarkasteltujen havainnollistavan tapauksen määrityskerroin osoittautui 0.98. Toisin sanoen lineaarinen säätö funktion kautta:

 f (x) = 2.1x - 1

On 98% luotettava selittää tiedot, joiden avulla se saatiin vähimmäisnopeuden avulla. 

Määrityskertoimen lisäksi on olemassa Lineaarinen korrelaatiokerroin tai tunnetaan myös nimellä Pearson -kerroin. Tämä kertoimet, nimeltään r -, Se lasketaan seuraavalla suhteella:

R = sxy / (SX SY)

Tässä numeroija edustaa muuttujien X ja Y.

Pearsonin kerroin voi ottaa arvot välillä -1 ja +1. Kun tämä kerroin on yleensä +1, x: n ja y: n välillä on suora lineaarinen korrelaatio. Jos sen sijaan sillä on -1, on lineaarista korrelaatiota, mutta kun X kasvaa ja vähenee. Lopuksi se on lähellä 0: ta, kahden muuttujan välillä ei ole korrelaatiota.

Voi palvella sinua: Ryhmittynyt data: Esimerkkejä ja liikunta ratkaistu

On huomattava, että määrityskerroin osuu samanaikaisesti Pearson -kertoimen neliön kanssa, vain kun ensimmäinen on laskettu lineaarisen säädön perusteella, mutta tämä tasa -arvo ei ole pätevä muihin epälineaarisiin säätöihin.

Esimerkit

- Esimerkki 1

Ryhmä lukion oppilaita aikoo määrittää heilurin ajan empiirisen lain sen pituuden funktiona. Tämän tavoitteen saavuttamiseksi he tekevät mittasarjan, jossa ne mittaavat heilurin värähtelyn ajan eri pituisille, jotka saavat seuraavat arvot:

Pituus (m)	Ajanjakso (t)
0,1	0,6
0,4	1.31
0,7	1,78
1	1.93
1.3	2.19
1.6	2.66
1.9	2,77
3	3.62

Tietojen dispersiokaavio pyydetään tekemään lineaarinen säätö regressiolla. Näytä lisäksi regressioyhtälö ja sen määrityskerroin.

Ratkaisu

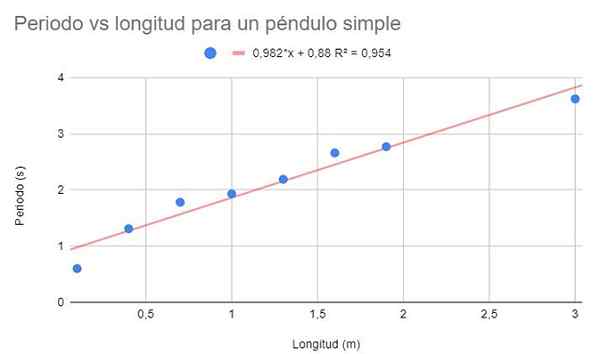Kuva 2. Harjoituksen 1 graafinen ratkaisu. Lähde: f. Zapata.

Melko korkea määrityskerroin (95%) voidaan havaita, joten voidaan ajatella, että lineaarinen säätö on optimaalinen. Kuitenkin, jos pisteitä havaitaan yhdessä, näyttää siltä, ​​että niillä on taipumus kaareutua. Tätä yksityiskohtaa ei harkita lineaarisessa mallissa.

- Esimerkki 2

Tee esimerkiksi 1 samoille tietoille datan dispersiokaavio. Tässä yhteydessä, toisin kuin esimerkki 1, sitä pyydetään tekemään regression säätö potentiaalisen funktion kautta.

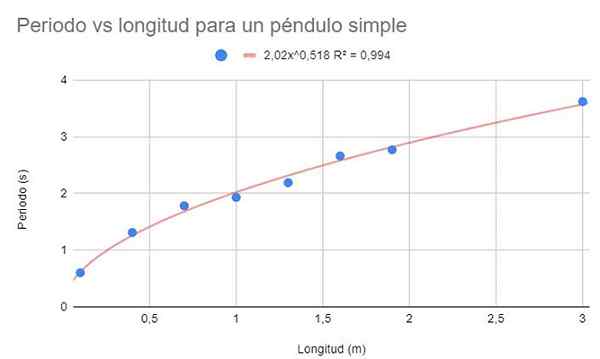Kuva 3. Harjoituksen 2 graafinen ratkaisu. Lähde: f. Zapata.

Näytä myös säätötoiminto ja sen R -määrityskerroin².

Ratkaisu

Potentiaalinen funktio on muodoltaan f (x) = ax^{B -}, missä a ja b ovat vakioita, jotka määritetään vähimmäismenetelmällä.

Edellinen kuva näyttää potentiaalisen funktion ja sen parametrit, samoin kuin määrityskerroksen erittäin korkealla arvolla 99%. Huomaa, että tiedot seuraavat trendilinjan kaarevuutta.

Voi palvella sinua: Lisäaineperiaate

- Esimerkki 3

Tee esimerkiksi 1 ja esimerkillä 2 samoilla tiedoilla toisen asteen polynomin säätö. Näytä kaavio, säätöpolynomi ja määrityskerroin r² kirjeenvaihtaja.

Ratkaisu

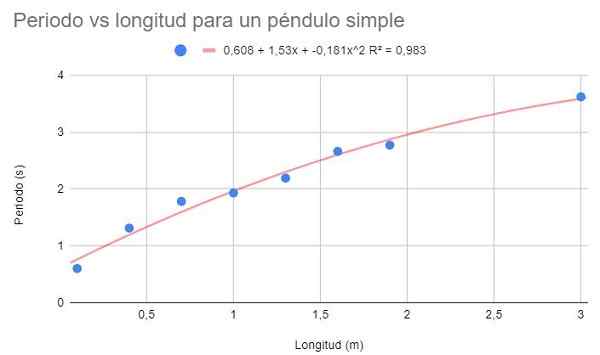Kuva 4. Graafinen harjoitus 3 -kuvaaja. Lähde: f. Zapata.

Toisen asteen polynomin säätäessä voidaan nähdä suuntaus, joka sopii hyvin tietojen kaarevuuteen. Samoin määrityskerroin on lineaarisen säädön yläpuolella ja mahdollisen säädön alapuolella.

Säätövertailu

Kolmesta esitetystä säädöksestä, jolla on korkeampi määrityskerroin, on potentiaalinen säätö (esimerkki 2).

Mahdollinen sopeutuminen on samaan aikaan heilurin fyysisen teorian kanssa, joka, kuten tiedetään, osoittaa, että heilurin ajanjakso on verrannollinen sen pituuden neliöjuureen, joka on suhteellisuusvakio 2π /√g, missä g on kiihtyvyys painovoima.

Tämän tyyppisellä mahdollisella säädöllä ei ole vain korkein määrityskerroin, vaan eksponentti- ja suhteellisuusvakiot ovat samat fyysisen mallin kanssa. 

Päätelmät

-Regression säätö määrittelee funktion parametrit, jotka pyrkivät selittämään tiedot minimin neliömenetelmällä. Tämä menetelmä koostuu arvon ja säädön ja datan Yi -arvon kvadraattisen eron summan minimoimisesta datan XI -arvojen välillä. Tällä tavoin määritetään säätöfunktion parametrit.

-Kuten olemme nähneet, yleisin säätöfunktio on viiva, mutta se ei ole ainoa, koska säädöt voivat olla myös polynomisia, potentiaalisia, eksponentiaalisia, logaritmeja ja muita. 

-Joka tapauksessa määrityskerroin riippuu tiedoista ja säätötyypistä ja osoittaa käytetyn säädön hyvyydestä.

-Lopuksi, määrityskerroin osoittaa arvon ja tietojen välisen kokonaisvariaation prosentuaalisen määrän suhteessa annetun X: n säädön arvoon.

Viitteet

1. González c. Yleiset tilastot. Toipunut: Tarwi.La Molina.Edu.PE -PE
2. IACS. Aragonese Institute of Health Sciences. Haettu: ICS-Aragon.com
3. Salazar C. ja Castillo S. Perustilastot periaatteet. (2018). Haettu osoitteesta: dspace.Uce.Edu.EY
4. Superprof. Määrityskerroin. Toipunut: SuperProf.On
5. USAC. Kuvaileva tilastokäsikirja. (2011). Palautettu: Tilastot.tekniikka.USAC.Edu.GT.
6. Wikipedia. Määrityskerroin. Palautettu: on.Wikipedia.com.