Ryhmittuneiden tietokaavojen, harjoitusten keskeisen taipumuksen mittaukset

Se trenditoimenpiteet keskeinen Ne osoittavat arvon, jonka ympärille jakauman tiedot ovat. Tunnetuin on keskimääräinen tai aritmeettinen keskiarvo, joka koostuu kaikkien arvojen lisäämisestä ja tuloksen jakaminen datan kokonaismäärällä.

Jos jakauma koostuu kuitenkin suuresta määrästä arvoja eikä sitä esitetä järjestämällä.

Kuvio 1. Ryhmittelemän datan keskeiset taipumusmittaukset ovat hyvä osoitus yleisestä tietojen käyttäytymisestä

Siksi ne on ryhmitelty luokkiin tai luokkiin, jotta voidaan tarkentaa a kuin Taajuudet. Suorittamalla tämä aikaisempi tietojärjestys, on helpompaa laskea keskeiset taipumusmittaukset, joista on:

-Puoli

-Mediaani

-Muoti

-Geometrinen keskiarvo

-Harmoninen keskiarvo

Kaavat

Alla on ryhmiteltyjen tietojen keskeisten taipumusmittausten kaavat:

Aritmeettinen keskiarvo

Keskiarvo on eniten käytetty kvantitatiivisten tietojen karakterisoimiseen (numeeriset arvot), vaikka se on melko herkkä äärimmäisille jakautumisarvoille. Se lasketaan:

Kanssa:

-X: Keskimääräinen tai keskimääräinen aritmeettinen

-F_Yllyttää: luokkataajuus

-m_Yllyttää: Luokan tuotemerkki

-G: Tunnin numero

-N: Kokonaistiedot

Mediaani

Sen laskemiseksi on tarpeen löytää aika, joka sisältää havainnon N/2 ja Interpolarin määrittämiseksi mainitun havainnon numeerisen arvon määrittämiseksi seuraavan kaavan avulla:

Missä:

-C: Välileveys, johon mediaani kuuluu

-B -_M: mainitun aikavälin alaraja

-F_m: Aikaväliin sisältyvien havaintojen lukumäärä

-N/2: Kokonaistiedot jaettuna 2: lla.

-F_Bm: havaintojen lukumäärä ennen mediaania sisältävää aikaväliä.

Siksi mediaani on sijaintimitta, ts. Jaako tietojoukko kahteen osaan. Ne voidaan myös määritellä kvartiilit, Desilit ja prosentti, jotka jakautuvat jakauman neljään, kymmeneen ja sataan osaan.

Voi palvella sinua: Fourier -muunnos: Ominaisuudet, sovellukset, esimerkit

Muoti

Ryhmitetyissä tiedoissa etsitään suurimman osan havainnoista, jotka sisältävät suurimman osan havainnoista. Tämä on Modaaliluokka. Jakaudella voi olla kaksi tai useampia muotoja, jolloin sitä kutsutaan bimodaalinen ja Multimodaalinen, vastaavasti.

Voit myös laskea muodin ryhmiteltyihin tietoihin yhtälön jälkeen:

Kanssa:

-Lens₁: Luokan alaraja, jossa muoti on

-Δ₁: Se pysyy modaaliluokan taajuuden ja sitä edeltäneen luokan taajuuden välillä.

-Δ₂: Vähennä modaaliluokan taajuuden ja sitä seuraavan luokan taajuuden välillä.

-C: Välileveys, joka sisältää muotia

Harmoninen keskiarvo

Harmoninen keskiarvo merkitään h. Kun sinulla on joukko n arvot x₁, x₂, x₃…, Harmoninen keskiarvo on arvojen käänteisen keskiarvon käänteinen tai vastavuoroinen.

On helpompaa nähdä se kaavan läpi:

Ja kun sinulla on ryhmitelty tieto, lauseke muuttuu:

Missä:

-H: Harmoninen keskiarvo

-F_Yllyttää: luokkataajuus

-m_Yllyttää: Luokkabrändi

-G: Tunnin numero

-N = f₁ + F₂ + F₃ +..

Geometrinen keskiarvo

Jos sinulla on n Positiiviset numerot x₁, x₂, x₃…, Sen geometrinen keskiarvo lasketaan kaikkien numeroiden tuotteen n-EA: lla:

Ryhmittyjen tietojen tapauksessa voidaan osoittaa, että geometrisen keskimääräisen log g: n desimaalimyrsky on antanut:

Missä:

-G: Geometrinen keskiarvo

-F_Yllyttää: luokkataajuus

-m_Yllyttää: Luokan tuotemerkki

-G: Tunnin numero

-N = f₁ + F₂ + F₃ +..

H, G ja X välinen suhde

On aina totta, että:

H ≤ g ≤ x

Useimmat käytetyt määritelmät

Seuraavat määritelmät ovat välttämättömiä edellisissä kaavoissa kuvattujen arvojen löytämiseksi:

Taajuus

Taajuus määritellään, kuinka monta kertaa tosiasia toistetaan.

Etäisyys

Se on eroa pääaineen ja pienen arvon välillä, joka on läsnä jakautumisessa.

Luokkien lukumäärä

Tiedämme, kuinka monta luokkaa ryhmittelemme, käytämme joitain kriteerejä, esimerkiksi seuraavat:

Voi palvella sinua: 17 perusteltu ongelmaa

Rajat

Kunkin luokan tai aikavälin ääriarvoja kutsutaan rajat ja jokaisella luokalla voi olla molemmat hyvin määriteltyjä rajoja, jolloin sillä on alaraja ja yksi suurempi. Tai sillä voi olla avoimia rajoja, kun etäisyys annetaan, esimerkiksi tietyn lukumäärän suurempien tai pienempien arvojen.

Luokan tuotemerkki

Se koostuu yksinkertaisesti aikavälin keskipisteestä ja lasketaan keskimäärin ylärajan ja alarajan keskiarvo.

Intervallileveys

Tiedot voidaan ryhmitellä luokkiin, joiden koko on yhtä suuri tai eri koko, tämä on leveys tai amplitudi. Ensimmäinen vaihtoehto on eniten käytetty, koska se helpottaa laskelmia, vaikka joissain tapauksissa on välttämätöntä, että luokat ovat erilaiset leveys.

Leveys c Sävästä se voidaan määrittää seuraavalla kaavalla:

C = alue / n_c

Missä_c Se on luokkien lukumäärä.

Liikuntaa

Alla on sarja nopeusmittauksia km/h, joka on otettu tutkalla, joka vastaa 50 autoa, jotka kulkivat kadun läpi tietyssä kaupungissa:

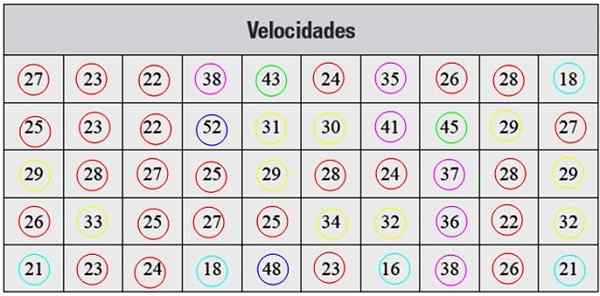Kuva 2. Taulukko harjoitusta varten. Lähde: f. Zapata.

Ratkaisu

Esitetyt tiedot eivät ole järjestetty, joten ensimmäinen askel on ryhmitellä ne luokkiin.

Vaiheet datan ryhmittelemiseksi ja taulukon rakentamiseksi

Vaihe 1

Etsi alue r:

R = (52 - 16) km/h = 36 km/h

Vaihe 2

Valitse luokkien lukumäärä n_c, Annetun kriteerin mukaan. Koska tietoja on 50, voimme valita n_c = 6.

Vaihe 3

Laske leveys c aikaväli:

C = alue /n_c = 36/6 = 6

Vaihe 4

Lomoluokit ja ryhmätiedot seuraavasti: Ensimmäisen luokan A alaraja valitaan heti, kun taulukossa oleva alempi arvo lisätään tähän arvoon c = 6, aikaisemmin laskettu, ja se saa siten ylärajan ensimmäinen luokka.

Se etenee samalla tavalla rakentaa loput luokat, kuten seuraavassa taulukossa on esitetty:

Voi palvella sinua: mikä on Capicúa -numero? Ominaisuudet ja esimerkit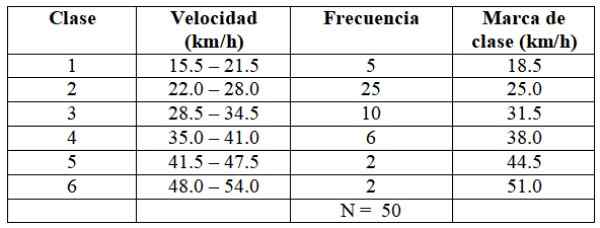

Jokainen taajuus vastaa kuviossa 2 olevaa väriä, tällä tavoin varmistetaan, että arvoa ei ole poistunut siitä.

Keskimääräinen laskenta

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Mediaanilaskelma

Mediaani on taulukon 2 luokassa, koska on olemassa ensimmäiset 30 jakelutietoa.

-Välileveys, johon mediaani kuuluu: C = 6

-Alivälin alaraja, jossa mediaani on: b_M = 22.0 km/h

-Aikavälillä F -havaintojen lukumäärä_m = 25

-Kokonaistiedot jaettuna 2: 50/2 = 25

-Havaintojen lukumäärä ennen mediaania sisältävää aikaväliä: f_Bm = 5

Ja toiminta on:

Mediaani = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/h

Muoti

Muoti löytyy myös luokasta 2:

-Välileveys: C = 6

-Luokan alaraja, josta löytyy muoti: l₁ = 22.0 -

-Vähennä modaaliluokan taajuuden ja sitä edeltäneen luokan taajuuden välillä: δ₁ = 25-5 = 20

-Vähennä modaaliluokan taajuuden ja seuraavan luokan taajuuden välillä: δ₂ = 25 - 10 = 15

Näiden tietojen kanssa toiminta on:

Muoti = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/h

Geometrisen keskiarvon laskeminen

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x log 38 + 2 × log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/h

Harmoninen keskimääräinen laskenta

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/h

Yhteenveto keskeisistä taipumustoimenpiteistä

Muuttujayksiköt ovat km/h:

-Media: 29.03

-Mediaani: 26.80

-Muoti: 25.40

-Geometrinen media: 28.13

-Harmoninen keskiarvo: 27.32

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
4. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
5. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
6. Ryhmitetyn tiedon hoito. Toipunut: Itchihuahua.Edu.MX.
7. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.