Kvasiivisuuskaava ja yhtälöt, esimerkit, liikunta

Se kvasiivinen arvio, Kvasi -varianssi tai epäterveellinen varianssi on tilastollinen mitta a näyte Suhteessa. Näyte puolestaan ​​koostuu suuresta maailmankaikkeudesta otetusta tietosarjasta, nimeltään väestö.

Sitä merkitään monin tavoin, tässä se on valittu s_c² Ja sen laskemiseksi seuraava kaava seuraa:

Kuvio 1. Lähestymisen määritelmä. Lähde: f. Zapata.

Missä:

-s_c ² = näytteen kvaasirianssi tai varianssi (näytteen varianssi)

-x_Yllyttää = Jokainen näytetieto

-n = havaintojen lukumäärä

-X = Näytteen keskiarvo

Koska näytteen yhtenäisyys lähestymisessä on sen yksikön neliö, johon näyte tulee, tulosten tulkitsemisen yhteydessä se on parempi työskennellä kvasi -standardipoikkeama tai näytteen keskihajonta.

Tämä on merkitty nimellä s_c Ja se saadaan purkamalla kvasivarianssin neliöjuuri:

s_c = √ s_c ²

Kvaasirianssi on samanlainen kuin varianssi s², ainoalla erolla, että sen nimittäjä on N-1, kun taas varianssissa se on jaettu vain n. On selvää, että kun n on erittäin suuri, molempien arvot ovat yleensä samat.

Kun kvaasirianssin arvo tunnetaan, voit heti tietää, että varianssi.

[TOC]

Esimerkkejä lähestymyydestä

Haluat tietää minkä tahansa väestön ominaisuudet: ihmiset, eläimet, kasvit ja yleensä kaikenlaiset esineet. Mutta koko väestön analysointi ei välttämättä ole helppo tehtävä, varsinkin jos elementtien lukumäärä on erittäin suuri.

Sitten otetaan näytteet toivoen, että heidän käyttäytymisensä heijastaa väestön käyttäytymistä ja siten kykenevää päätelmään siitä, mitkä resurssit on optimoitu. Tämä tunnetaan nimellä tilastollinen päätelmä.

Tässä on joitain esimerkkejä, joissa kvaasirianssi ja kvaasiin liittyvä keskihajonta toimivat tilastollisena indikaattorina huomauttamalla, että saadut tulokset suhteessa keskiarvoon nähden.

Se voi palvella sinua: ympyrän kehä: Kuinka ottaa se pois ja kaavat, ratkaistut harjoitukset

1.- Auton paristoja valmistavan yrityksen markkinointijohtajan on arvioitava kuukausina keskimääräisen akun kesto.

Jos haluat tehdä tämän, valitse satunnaisesti 100 tuotemerkin näyte,. Yhtiö säilyttää tietueen ostajien tiedoista ja voi haastatella niitä tietämään paristojen keston.

Kuva 2. Cuasivis Apprives on hyödyllinen päätelmien ja laadunvalvonnan tekemisessä. Lähde: Pixabay.

2.- Yliopistolaitoksen akateemisen johdon on arvioitava seuraavan vuoden rekisteröinti analysoimalla niiden opiskelijoiden lukumäärää, joiden odotetaan hyväksyvän tällä hetkellä olevat aiheet.

Esimerkiksi jokaisesta fyysistä aihetta tutkittavista osioista osoite voi valita opiskelijoiden otoksen ja analysoida sen suorituskykyä mainitussa puheenjohtajana. Tällä tavoin voit päätellä, kuinka moni opiskelija opiskelee fysiikkaa II seuraavana ajanjaksona.

3.- Ryhmä tähtitieteilijöitä keskittää huomionsa taivaan osaan, jossa havaitaan tietty määrä tähtiä, joilla on tiettyjä ominaisuuksia: esimerkiksi koko, massa ja lämpötila.

On syytä kysyä, onko toisella samanlaisella alueella tähtiä samat ominaisuudet, mukaan lukien tähdet muissa galakseissa, kuten Magallanesin tai Andromedan viereiset pilvet.

Miksi jakaa N-1: n välillä?

Kvaasirianssissa se on jaettu keskenään N-1 sijasta n Ja se johtuu siitä, että kvaasirianssi on a Vaatia arvioijaa, Kuten alussa todettiin.

Se tapahtuu, että samasta populaatiosta on mahdollista purkaa monia näytteitä. Kummankin näytteen varianssi voidaan myös keskiarvoa, mutta näiden varianssien keskiarvo ei osoittaudu yhtä suureksi kuin populaation varianssi.

Voi palvella sinua: suhteellinen arvo

Itse asiassa otoksen varianssien keskiarvo pyrkii aliarvioimaan populaation varianssia, ellei sitä käytetä N-1 Nimittäjässä. Voidaan varmistaa, että odotettu arvo kvasiivisuudesta E (S_c²) on tarkalleen s².

Siksi sanotaan, että kvaasirianssi on insensted ja on parempi arviointi väestövarianssista S².

Vaihtoehtoinen tapa laskea kvasiivinen arvio

On helposti osoitettu, että kvaasirianssi voidaan myös laskea seuraavasti:

s_c² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Vakiopiste

Poikkeamalla näytteestä voimme tietää, kuinka monella standardipoikkeamalla on tietty arvo X, joko keskiarvon ylä- tai alapuolella.

Tätä varten käytetään seuraavaa ulottumatonta lauseketta:

Standard -pistemäärä = (x - x) / s_c

Liikuntaa

Laske seuraavien tietojen kvaasirianssi ja kvasi -tyypillinen poikkeama, joka koostuu kuukausittaisista maksuista, jotka vakuutusyhtiö on suorittanut yksityiselle klinikalle.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Käytä alussa annetun lähestymisen määritelmää ja tarkista tulos myös edellisessä osassa annetulla vaihtoehtoisella muodolla.

b) Laske toisen datan vakiopiste, lukemalla ylhäältä alas.

Liittää jhk

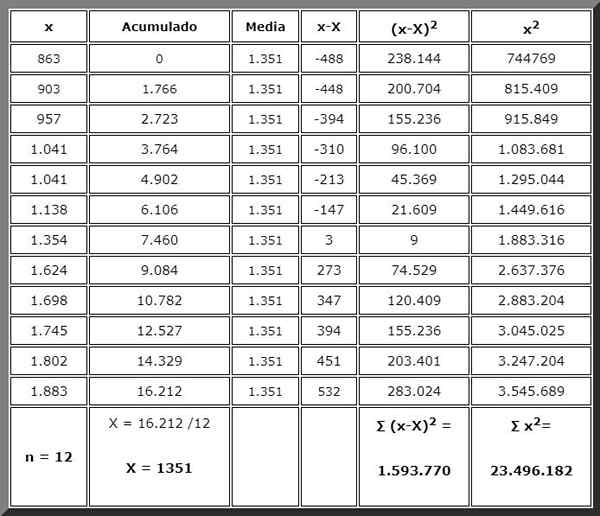
Ongelma voidaan ratkaista käsin yksinkertaisen tai tieteellisen laskimen avulla, jolle meidän on jatkettava järjestyksessä. Ja tälle ei ole mitään parempaa kuin alla olevan taulukon järjestäminen alla esitetyllä tavalla:

Järjestämäsi taulukon ansio. Yhteenveto on merkitty lihavoituna.

Voi palvella sinua: mitkä ovat kehän 7 elementtiä?

Keskimääräinen sarake toistetaan aina, mutta se on sen arvoista.

Lopuksi, alussa annetun kvaasirianssin yhtälöä sovelletaan, vain arvot korvataan ja summan suhteen meillä on jo se laskettu:

s_c² = 1.593.770 / (12-1) = 1.593.770/11 = 144.888.2

Tämä on kvaasirianssin arvo ja sen yksiköt ovat ”Dollars Squared”, jolla ei ole paljon käytännöllistä järkeä, joten näytteen vakiokvaasidit lasketaan, mikä ei ole muuta kuin kvaasivarianssin neliöjuuri:

s_c = (√144.888,2) $ = 380,64 $

Vahvistetaan heti, että tämä arvo saadaan myös kvasivarianssin vaihtoehtoisella muodolla. Tarvittava summa on viimeisen sarakkeen lopussa:

s_c² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ yksitoista]

= 2.136.016.55 - 1.991.128,36 = 144.888 dollaria neliö

Se on sama arvo, joka on saatu alussa annetulla kaavalla.

Ratkaisu b

Toinen arvo ylhäältä alas on 903, sen vakiopiste on

Vakiopiste 903 = (x - x) / s_c = (903 - 1351)/380.64 = -1.177

Viitteet

1. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
4. Dispersion mitat. Toipunut: Thales.CICA.On.
5. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.