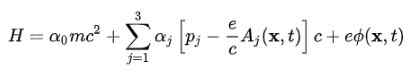Dirac Jordan -ominaisuuksien ja postulaattien AOMIC -malli

Hän Dirac-Jordan Atom -malli Hamiltonin operaattorin relativistinen yleistäminen yhtälössä kuvaavat kvantti -aaltofunktiota. Toisin kuin edellisessä malli, Schrodinger, ei ole välttämätöntä asettaa spiniä Paulin syrjäytymisperiaatteen kautta, koska se näyttää luonnollisesti.

Lisäksi Dirac-Jordan-malli sisältää relativistiset korjaukset, spin-organ-vuorovaikutuksen ja Darwinin termin, jotka vastaavat atomin elektronisten tasojen hienoa rakennetta.

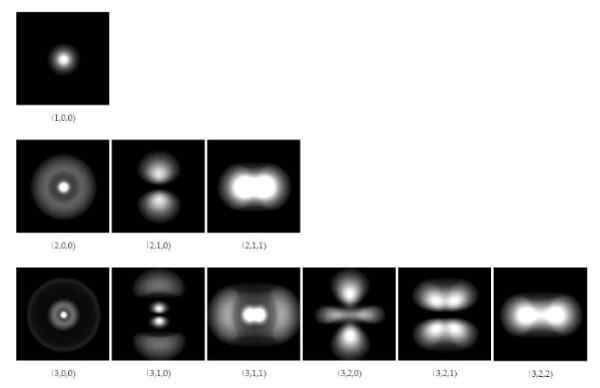
Kuvio 1. Kolmen ensimmäisen energiatason elektroniset kiertoradat vetyatomiin. Lähde: Wikimedia Commons.

Vuodesta 1928 lähtien tutkijat Paavali A. M. Dirac (1902-1984) ja Pascual Jordania (1902-1980) ehdotettiin Schrodingerin kehittämän kvantimekaniikan yleistämiseksi Einsteinin erityiselokuvien korjausten sisällyttämiseksi.

Dirac -osa Schrodinger -yhtälöstä, joka koostuu differentiaalioperaattorista, nimeltään Hamiltonian, joka toimii nimellä Elektroniaaltofunktio. Schrodinger ei kuitenkaan ottanut huomioon relativistisia vaikutuksia.

Aaltofunktioliuokset sallivat laskea alueet, joilla ytimen ympärillä oleva elektroni löytyy tietyllä todennäköisyydellä. Näitä alueita tai alueita kutsutaan Kiertoradat Ja ne riippuvat tietyistä erillisistä kvanttilukuista, jotka määrittelevät elektronin energian ja kulmanmomentin. 

[TOC]

Postulaatit

Kvanttimekaanisissa teorioissa riippumatta. Ja lisäksi yhden muuttujien määritteleminen johtaa toisessa epätarkkuuteen.

Hamiltonian puolestaan ​​on matemaattinen operaattori, joka toimii kvantti -aaltofunktioon ja on rakennettu elektronienergiasta. Esimerkiksi ilmaisella elektronilla on täydellistä energiaa ja se riippuu sen lineaarisesta vauhdista p täten:

E = (p²)/ 2M

Hamiltonian rakentamiseksi se alkaa tästä ilmaisusta ja korvataan p Kvanttioperaattorilla vauhtia varten: 

p = -I ħ ∂ /∂r - 

On tärkeää huomata, että termit p ja p Ne ovat erilaisia, koska ensimmäinen on vauhti ja toinen on Differentiaalioperaattori liittyy vauhtiin. 

Voi palvella sinua: Leukipo -atomimalli: postulaatit, rajoitukset, merkitys

Lisäksi I on kuvitteellinen yksikkö ja ħ Planck -vakio jaettuna 2π: llä, tällä tavalla saadaan Hamiltonian operaattori H:

H = (ħ²/2M) ∂² /∂r -² 

Löytääksesi atomin elektronin Hamiltonian, elektronien vuorovaikutus ytimen kanssa lisätään: 

H = (ħ2/2m) ∂² /∂r -²  - Eφ (r)

Edellisessä ekspressiossa -e on elektronien sähkövaraus ja φ (r) keskusydin tuottama sähköstaattinen potentiaali.

Nyt operaattori H toimii aaltofunktioon ψ Schrodinger -yhtälön mukaisesti, joka on kirjoitettu näin:

H ψ = (i ħ ∂ /∂t) ψ

Diracin neljä postulaatiota

Ensimmäinen postulaatti: Relativistisella aaltoyhtälöllä on sama rakenne kuin Schrodingerin aaltoyhtälö, mikä muuttuu H:

H ψ = (i ħ ∂ /∂t) ψ

Toinen postulaatti: Hamiltonian operaattori on rakennettu Einsteinin energia-momentumin suhteen, joka on kirjoitettu näin:

E = (m² c⁴ + p² c²-A^1/2

Edellisessä suhteessa, jos hiukkasella on vauhti p = 0, sinulla on kuuluisa yhtälö E = MC² joka yhdistää minkä tahansa massan m: n lepoenergian valon nopeuden kanssa.

Kolmas postulaatio: Hamiltonian operaattorin hankkimiseksi käytetään samaa kvantisointisääntöä, jota käytetään Schrodinger -yhtälössä:

p = -I ħ ∂ /∂r -

Alussa ei ollut selvää, kuinka käsitellä tätä neliöjuuren sisällä toimivaa differentiaalista operaattoria, joten Dirac päätti hankkia lineaarisen Hamiltonian operaattorin Momentum -operaattorissa ja sieltä syntyi hänen neljäs postulaatti.

Postilaite: Relativistisen energiakaavan neliöjuuren päästämiseksi Dirac ehdotti seuraavaa E -rakennetta E: lle²-

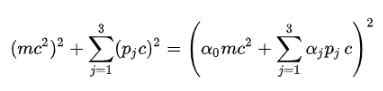
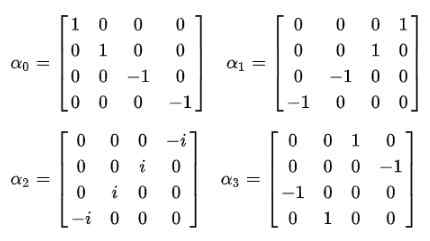
Tietysti on välttämätöntä määrittää alfa -kertoimet (a0, α1, α2, α3) siten, että tämä täyttyy.

Dirac -yhtälö

Dirac -yhtälö nostettiin ensin vapaalle elektronille käyttämällä neljännessä postulaatiossa ehdotettua rakennetta. Se pysyy seuraavasti: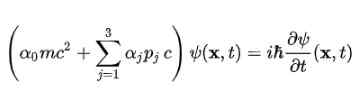

Se voi palvella sinua: Kuule voima: pinta- ja massavoimat

Kompaktissa muodossaan Dirac -yhtälöä pidetään yhtenä maailman kauneimmista matemaattisista yhtälöistä:

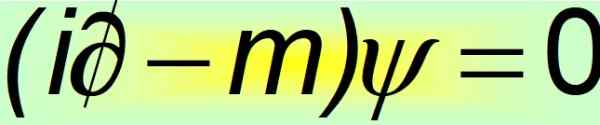Kuva 2. Dirac -yhtälö kompakti. Lähde: f. Zapata.

Ja silloin todistetaan, että vakio Alfas ei voi olla skalaarisia määriä. Ainoa tapa, jolla neljännen postulaatin tasa -arvo on täyttynyt, on, että ne ovat 4 × 4 vakiona, jotka tunnetaan Dirac -matriisit-

Heti havaitaan, että aaltofunktio lakkaa olemasta skalaarifunktio ja siitä tulee neljä -komponentti vektori Esteen-

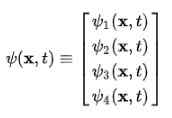
Dirac-Jordanin atomi

Atomismallin saamiseksi on tarpeen siirtyä vapaasta elektroniyhtälöstä atomiykkeellä tuottaman sähkömagneettisen kentän elektroniin. Tämä vuorovaikutus otetaan huomioon sisällyttämällä potentiaalinen skalaari φ ja potentiaalinen vektori -Lla Hamiltonian kielellä:

Aaltofunktiolla (Espinor), joka johtuu tämän Hamiltonian sisällyttämisestä, on seuraavat ominaisuudet: 

- Se täyttää erityisen suhteellisen suhteellisuuden, koska siinä otetaan huomioon elektronin luontainen energia (relativistisen Hamiltonian ensimmäinen termi)

- Siinä on neljä ratkaisua, jotka vastaavat Espinorin neljää komponenttia

- Kaksi ensimmäistä ratkaisua vastaavat yhtä spin +½ ja toinen spiniin - ½ 

- Lopuksi kaksi muuta ratkaisua ennustavat antimatterin olemassaolon, koska ne vastaavat vastakohtien positronien vastakohtia.

Dirac -yhtälön suuri etu on, että Schrodinger H (O): n Hamiltonin peruskorjaukset voidaan jakaa useisiin termeihin, jotka näytämme alla:

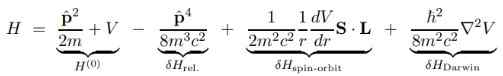
Edellisessä lausekkeessa V on potentiaalinen skalaari, koska potentiaalinen vektori -Lla Se on tyhjyyttä, jos sen oletetaan olevan keskitetylle paikallaan olevalle protonille, ja siksi se ei näy.

Syy siihen, miksi Diracin korjaukset Schrodinger -ratkaisuista aaltofunktiossa ovat hienovaraisia. Ne johtuvat siitä, että korjattu Hamiltonian kolme viimeistä termiä on jaettu neliön nopeudella C, valtava luku, joka tekee näistä termeistä numeerisesti pienet.

Se voi palvella sinua: Vy canis majoris: löytö, ominaisuudet, rakenne, koulutus ja evoluutio

Relativistiset korjaukset energiaspektriin

DIC-Jordan-yhtälöä käyttämällä korjauksia löytyy vetyatomin elektronien energiaspektriin. Atomien energiaa koskevia korjauksia on myös useamman kuin yhden elektronin kanssa suunnilleen häiriöiden teorian metodologian avulla.

Samoin DIRAC -malli antaa sinun löytää hienon rakenteen korjauksen vetyenergiatasoilla. 

Vielä hienovaraisempia korjauksia, kuten hyperfiinirakenne ja LAMB: n muutos, saadaan edistyneemmistä malleista, kuten Campos -kvanttiteoria, Syntynyt juuri Dirac -mallin panoksen vuoksi.

Seuraava kuva osoittaa, kuinka Diracin relativistiset korjaukset ovat energiatasoilla:

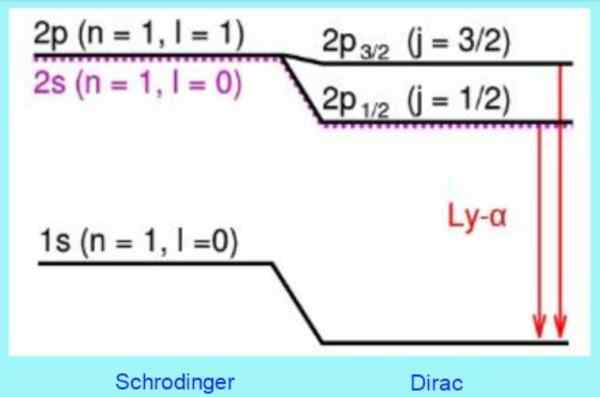Kuva 3. Dirac -mallin korjaukset vetyatomitasoilla. Lähde: Wikimedia Commons.

Esimerkiksi Dirac -yhtälöön liittyvät ratkaisut ennustavat oikein tasolla havaitun muutoksen. Se on hyvin tunnettu hienohakemuskorjaus vetypektrin Lyman -viivalla - Alfa (katso kuva 3).

Muuten, hieno rakenne on nimi, joka vastaanottaa atomifysiikassa atomien päästöspektrin linjojen avautumisen, mikä on suora seuraus elektronisesta spinistä.

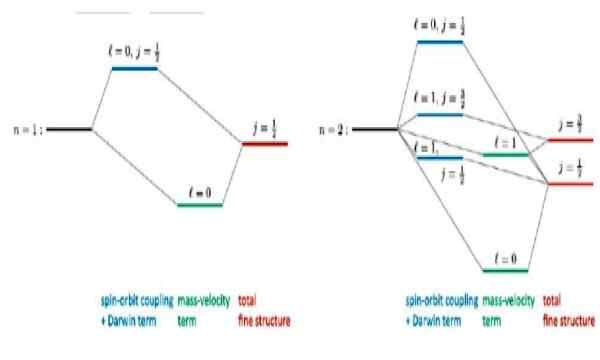Kuva 4. Hieno rakenne, joka avautuu perustilaan n = 1 ja ensimmäinen viritetty tila n = 2 vetyatomisessa. Lähde: R Wirnata. Relativistiset korjaukset vedyn kaltaisiin atomiin. Tutkimussarja.netto

Kiinnostavia artikkeleita

Broglie -atomimalli.

Chadwick Atomic -malli.

Heisenberg Atomic -malli.

Perrin Atomic -malli.

Thomson Atomic -malli.

Dalton Atomic -malli.

Schrödinger Atomic -malli.

Democritus Atomic -malli.

Leucpo -atomimalli.

Bohr -atomimalli.

Nykyinen atomimalli.

Viitteet

1. Atomiteoria. Toipunut Wikipediasta.org.
2. Elektronimagneettinen hetki. Toipunut Wikipediasta.org.
3. Quanta: käsikirja käsitteistä. (1974). Oxford University Press. Toipunut Wikipediasta.org.
4. Dirac Jordan Atomic -malli. Prezi.com.
5. Uusi kvanttien maailmankaikkeus. Cambridge University Press. Toipunut Wikipediasta.org.