Hitausmomentti, yhtälöt ja esimerkit laskennasta

Hän hitausmomentti Jäykästä rungosta tietyn kierto -akselin suhteen, se edustaa sen vastustuskykyä sen kulmanopeuden muuttamiselle kyseisen akselin ympärillä. Se on verrannollinen massaan ja myös kierto -akselin sijaintiin, koska runko geometrian mukaan voi helpommin pyöriä tiettyjen akselien ympärillä kuin muissa.

Oletetaan, että laaja esine (koostuu monista hiukkasista), joka voi pyöriä akselin ympäri. Oletetaan, että voima toimii F, Massaelementtiin sovellettu tangentiaalisesti ΔM_Yllyttää, joka tuottaa vääntömomentin tai hetken, jonka on annettu τ_netto = ∑r -_Yllyttää x F_Yllyttää. Vektori r -_Yllyttää Se on sijainti ΔM_Yllyttää (Katso kuva 2).

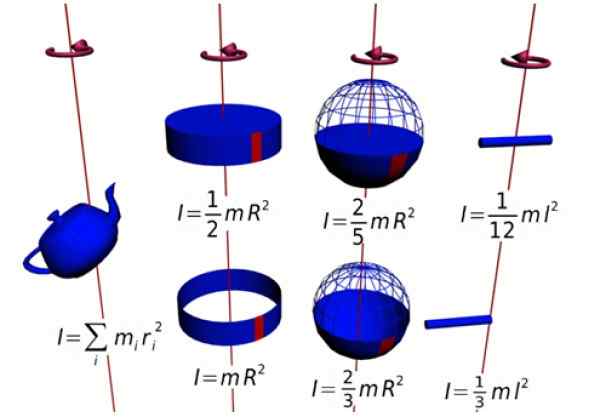
Kuvio 1. Useiden lukujen hitausmomentit. Lähde: Wikimedia Commons.

Tämä hetki on kohtisuorassa kiertotasoon (osoite +K = Lähde paperille). Koska lujuus ja säteittäinen sijainti ovat aina kohtisuorassa, ristin tuote pysyy:

τ_netto = ∑ f_Yllyttää r -_Yllyttää k -k - = ∑ (ΔM_Yllyttää -lla_Yllyttää) r_Yllyttää  k -k - = ∑ Δm_Yllyttää (_Yllyttää r -_Yllyttää -A k -k -

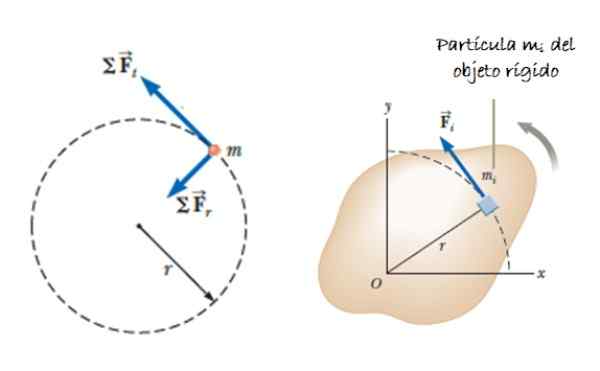Kuva 2. Hiukkas. Lähde: Serway, R. 2018. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Cengage -oppiminen.

Kiihtyvyys a_Yllyttää edustaa kiihtyvyyden tangentiaalista komponenttia, koska radiaalinen kiihtyvyys ei vaikuta vääntömomenttiin. Kulmakiihtyvyydestä α riippuen voimme osoittaa, että:

-lla_Yllyttää = α R_Yllyttää

Siksi nettomomentti on tällainen:

τ_netto = ∑ Δm_Yllyttää (α R_Yllyttää²-A K = (∑ r -_Yllyttää² ΔM_Yllyttää) α k -k -

Kulmakiihtyvyys α on sama koko objektille, joten alaindeksi "I" ei vaikuta siihen, ja se voi jättää summan, mikä on juuri symboloidun esineen hitausmomentti I -kirjaimella:

I = ∑ r_Yllyttää² ΔM_Yllyttää

Tämä on erillisen massajakauman hitausmomentti. Kun jakauma on jatkuvaa, summa korvataan olennaisella ja ΔM tulee massaero Dm. Integraali tehdään ennen kaikkea esinettä:

I = ∫_M(R²) DM

Kansainvälisen järjestelmän hitaushetken yksiköt, jos ne ovat Kg x m². Se on skalaari ja positiivinen määrä, koska se on taikinan tuote etäisyyden neliöllä.

[TOC]

Esimerkkejä laskelmasta

Laajennettu esine, kuten palkki, levy, pallo tai muu, jonka tiheys ρ Se on vakio ja tietäen, että tiheys on massa -volyymi -osuus, massaero Dm Se on kirjoitettu seuraavasti:

ρ = dm/dv → dm = ρDV

Korvataan inertiahetken integraaliin, meillä on:

I = ∫r² ρdv = ρ ∫r²DV

Tämä on yleinen lauseke, joka on voimassa kolmiulotteiselle objektille, jonka tilavuus V asento r - Ne ovat avaruuskoordinaattien funktioita x, ja ja z -z. Huomaa, että vakiona tiheys on pois olennaisesta.

Tiheys ρ Sitä kutsutaan myös tilavuustiheydeksi, mutta jos esine on erittäin tasainen, arkkina tai erittäin ohut ja kapea kuin sauva, voidaan käyttää muita tiheysmuotoja, katsotaan:

Voi palvella sinua: Maan kiertoliike

- Erittäin hienolla arkilla käytettävä tiheys on σ, pintatiheys (massa yksikköä kohti) ja antaa on alueero.

- Ja jos se on ohut palkki, jossa vain pituus on merkityksellinen, käytetään lineaarista massan tiheyttä λ ja pituusero, viitteenä käytetyn akselin mukaan.

Seuraavissa esimerkeissä kaikkia esineitä pidetään jäykkinä (ei -muodostumattomina) ja niillä on tasainen tiheys.

Ohuen palkin hitausmomentti suhteessa akseliin, joka kulkee sen keskuksen läpi

Täällä aiomme laskea ohuen, jäykän, homogeenisen palkin, pituuden l ja massa M: n hitausmomentin, suhteessa keinojen läpi kulkevaan akseliin.

Ensinnäkin on välttämätöntä luoda koordinaattijärjestelmä ja rakentaa luku, jolla on riittävä geometria, kuten tämä:

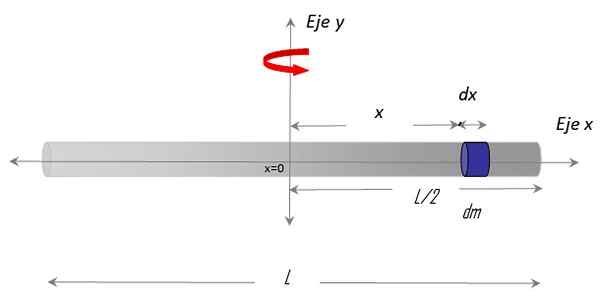Kuva 3. Geometria ohuen sauvan hitausmomentin laskemiseksi suhteessa pystysuoraan akseliin, joka kulkee sen keskustan läpi. Lähde: f. Zapata.

Hänet valittiin X -akseli tankoa ja Akseli y kierto -akselina. Integraalin määrittämismenettely vaatii myös massaeron valitsemista palkissa, nimeltään Dm, jolla on differentiaalipituus Dx ja sijaitsee asennossa x mielivaltainen, keskustaan x = 0.

Lineaarisen massan tiheyden määritelmän mukaan λ:

λ = m/l

Kun tiheys on tasainen, mikä pätee M: lle ja L: lle, se on myös DM: lle ja DX: lle:

λ = dm/dx → dm = λdx.

Toisaalta massaelementti on paikallaan x, Sitten korvaamalla tämän geometrian määritelmässä, meillä on selvä integraali, jonka rajat ovat palkin ääripäät koordinaattijärjestelmän mukaan:

Lineaarisen tiheyden korvaaminen λ = m/l:

Löydä palkin hitausmomentti toiseen pyörimisakseliin, esimerkiksi yhden sen päätä kulkevan läpi, voit käyttää Steiner -lausetta (katso lopussa oleva harjoitus) tai suorittaa suoran laskelman kuin se Näytetään tässä, mutta geometrian oikein muokkaaminen.

Albumin hitausmomentti suhteessa akseliin, joka kulkee sen keskuksen läpi

Erittäin ohut albumi, halveksittava paksuus on litteä hahmo. Jos taikina on jakautunut tasaisesti alueelle A, massan tiheys σ on:

σ = M/a

Niin paljon Dm kuten antaa vastaa kuviossa esitetyn differentiaalirenkaan massaa ja aluetta. Oletetaan, että koko sarja pyörii akselin ympäri ja.

Voit kuvitella, että albumi on säveltänyt, että monet radion samankeskiset renkaat r -, Jokainen hitaushetkellään. Kaikkien renkaiden panoksen lisääminen, kunnes saavutat radion R -, Sinulla on albumin kokonaishitaus.

σ = dm/da → dm = σantaa

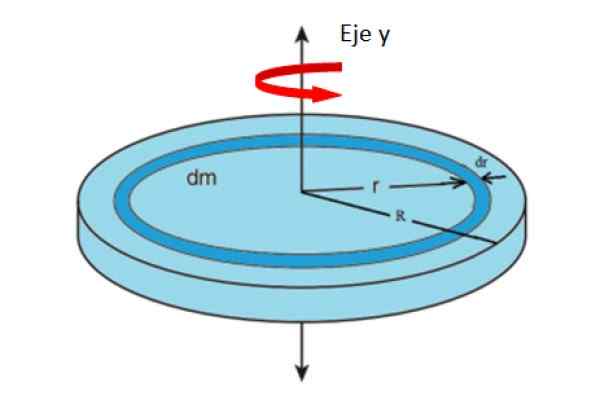Kuva 4. Geometria albumin hitausmomentin laskemiseksi aksiaalitakselin suhteen. Lähde: f. Zapata.

Missä m edustaa albumin koko taikinaa. Albumin alue riippuu sen säteesta R: llä:

Voi palvella sinua: aallon etenemisnopeus

A = π.r -²

Johdetaan noin r:

Da /dr = 2 = 2π.R → da = 2π.rdr

Edellä mainitun I: I: n korvaaminen: I:

Arvioinnin jälkeen olennaiset tulokset:

Korvaa σ = m/(π.R -² ) on jäljellä:

Kiinteän pallon hitausmomentti halkaisijan suhteen

Sädettä R -palloa voidaan pitää pinottuina levyinä toistensa päällä, missä kukin ääretön massaalbumi Dm, radio r - ja paksuus Dz, Sillä on hetki hitaus: Annetaan:

antaa_levy = (½) r²Dm

Tämän eron löytämiseksi edellisen osan kaava yksinkertaisesti otettiin ja korvattiin M ja R - ohella Dm ja r -, vastaavasti. Tällainen albumi näkyy kuvan 5 geometriassa.

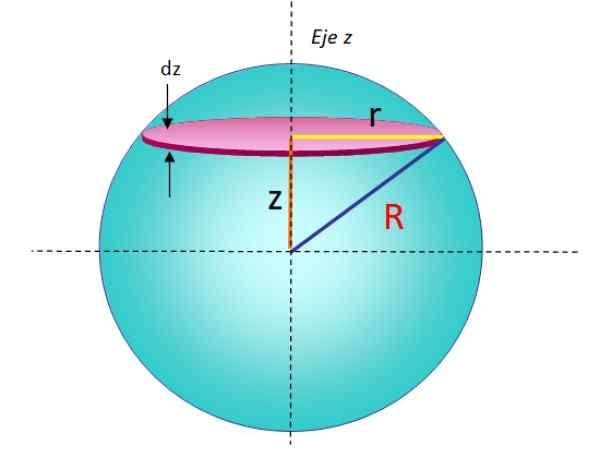Kuva 5. Geometria kiinteän sädepallon hitausmomentin laskemiseksi suhteessa halkaisijan läpi kulkevaan akseliin. Lähde: f. Zapata.

Lisäämällä kaikki pinottujen levyjen äärettömän vähäisen hitauden hetket, pallon kokonaishitauden hetki saadaan:

Yllyttää_pallo = ∫di_levy

Mikä vastaa:

I = ∫_pallo (½) r²Dm

Integraalin ratkaisemiseksi sinun on ilmaista Dm asianmukaisesti. Kuten aina, se saavutetaan tiheydestä:

ρ = m/v = dm/dv → dm = ρ.DV

Differentiaalilevyn tilavuus on:

DV = pohjapinta -ala x korkeus

Albumin korkeus on paksuus Dz, Vaikka perusalue on πr², siksi:

Dv = πr²Dz

Ja integroidun korvaaminen olisi näin:

I = ∫_pallo(½) r²Dm = ∫ (½) r²(ρπr²DZ)

Mutta ennen integroitua, sen täytyy. Pythagoras -lauseen kautta:

R -² = r² + z -z² → R² = R² - z -z²

 Se johtaa meidät:

I = ∫_pallo(½) ρ r²(πr²dz) = ∫_pallo(½) ρ π r⁴Dz= ∫_pallo(½) ρ π (r² - z -z²-A² Dz

Koko pallon integroimiseksi huomaamme, että z vaihtelee välillä -r ja r, siksi:

Sen tietäen ρ = m/v = m/[(4/3) πr³- Lopuksi se saadaan yksinkertaistamisen jälkeen:

Kiinteän sylinterin hitausmomentti aksiaaliakselin suhteen

Tälle objektille käytetään menetelmää, joka on samanlainen kuin palloon käytetty, vain tällä kertaa on helpompaa, jos sylinteri kuvitellaan radiolieriömäisiin kuoriin r -, paksuus DR ja korkeus H, Ikään kuin ne olisivat sipulin kerrokset.

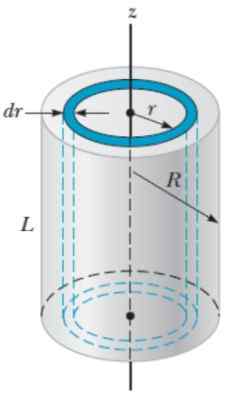Kuva 6. Geometria kiinteän säteen sylinterin r hitausmomentin laskemiseksi aksiaaliseen akseliin. Lähde: Serway, R. 2018. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Kyynärmä.

Äänenvoimakkuutta DV lieriömäinen kerros on:

DV = 2π.RL.DR

Siksi Cascaron -massa on:

Voi palvella sinua: Mikroskooppinen asteikko: Ominaisuudet, laskentapartikkelit, esimerkit

Dm = ρ.DV = ρ. 2π.r -.Lens.DR

Tämä lauseke korvataan hitausmomentin määritelmässä:

 Olettaen että ρ = m / (π.R -²L) on jäljellä:

Aikaisempi yhtälö osoittaa, että sylinterin hitausmomentti ei riipu sen pituudesta, vaan vain sen massasta ja vain säteestä. Joo Lens muuttunut, hitausmomentti aksiaaliseen akseliin olisi edelleen sama. Tästä syystä, Yllyttää sylinteristä osuu aikaisemmin lasketun ohuen albumin kanssa.

Suorakulmaisen arkin hitausmomentti suhteessa akseliin, joka kulkee sen keskuksen läpi

Se Akseli y Vaakasuora kierto -akselina. Seuraava kuva näyttää tarvittavan geometrian integraation suorittamiseksi:

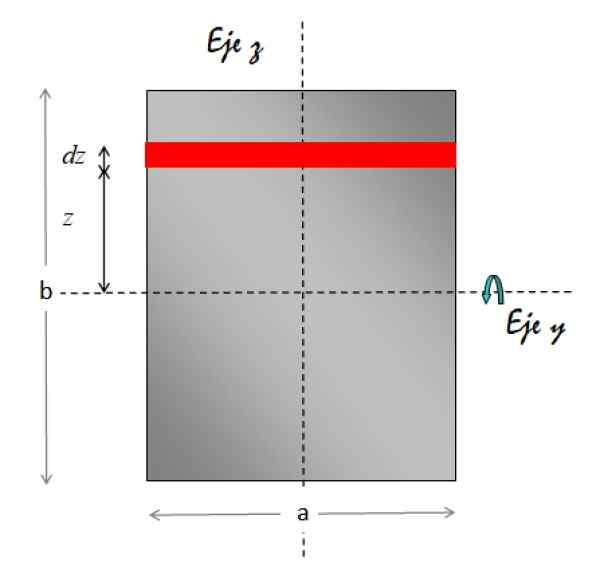Kuva 7. Geometria suorakaiteen muotoisen levyn hitausmomentin laskemiseksi arkin yhdensuuntaisen akselin suhteen ja se kulkee sen keskustan läpi. Lähde: f. Zapata.

Punaisella osoitettu alueelementti on suorakaiteen muotoinen. Sen pinta -ala on siis base x korkeus, siksi:

da = a.Dz

Siksi massaero on:

DM = σ.da = σ.(.DZ)

Mitä tulee alueen elementin etäisyydelle kierto -akselille, se on aina z -z. Korvaamme kaiken tämän hitausmomentin olennaisesti:

Nyt pintamassan tiheys σ korvataan:

σ = m/ab

Ja se on ehdottomasti tällainen:

Huomaa, että se on kuin ohut palkki.

Neliölevyn hitausmomentti suhteessa akseliin, joka kulkee sen keskuksen läpi

Neliölle sivulla Lens, Edellisessä suorakulmiossa voimassa olevassa lausekkeessa b - yksi Lens-

Hitaushetken lauseet

On olemassa kaksi erityisen hyödyllistä lausetta, jotka yksinkertaistavat hitausmomenttien laskemista muihin akseliin, joita muuten voisi olla monimutkainen löytää symmetrian puutteesta. Nämä lauseet ovat:

Steinerin lause

Kutsutaan myös rinnakkaisakselin lause, Yhdistää akselin hitausmomentin toisen kanssa, joka kulkee esineen massakeskuksen läpi, kunhan akselit ovat yhdensuuntaiset. Sen soveltamiseksi etäisyys D on tiedettävä kahden akselin ja tietysti esineen massa M: n välillä.

Olla Yllyttää_{z -z} laajennetun esineen hitaushetki Z, i -akseli_Cm Hitausmomentti suhteessa akseliin, joka kulkee mainitun esineen massan keskuksen (cm) läpi, niin täyttyy:

Yllyttää_{z -z} = I_Cm + MD²

Tai seuraavan kuvan merkinnässä: Yllyttää_{z '} = I_{z -z} + MD²

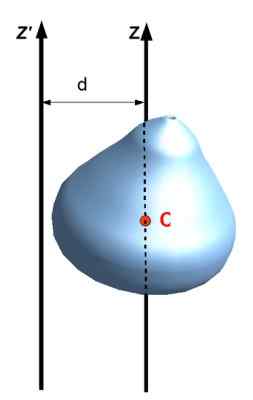Kuva 8. Steiner -lause tai rinnakkaiset akselit. Lähde: Wikimedia Commons. Jack Katso [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Kohtisuora -akselin lause

Tämä lause koskee tasaisia ​​pintoja ja sanoo: Siinä kohtisuoran akselin ympärillä olevan litteän esineen hitausmomentti on kahden akselin ympärillä olevien hitausmomenttien summa ensimmäiseen akseliin nähden:

Yllyttää_{z -z} = I_x + Yllyttää_ja

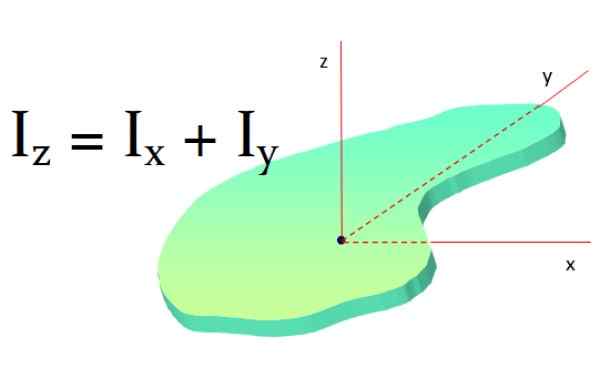Kuva 9. Kohtisuora -akselin lause. Lähde: f. Zapata.

Jos objektilla on symmetria niin Yllyttää_x ja Yllyttää_ja Ne ovat samoja, sitten on toteutettu, että:

Yllyttää_{z -z} = 2i_x

Liikuntaa

Löydä palkin hitausmomentti suhteessa akseliin, joka kulkee yhden sen päistä, kuten kuviossa 1 (alapuolella ja oikealla) ja kuva 10) ja kuva 10.

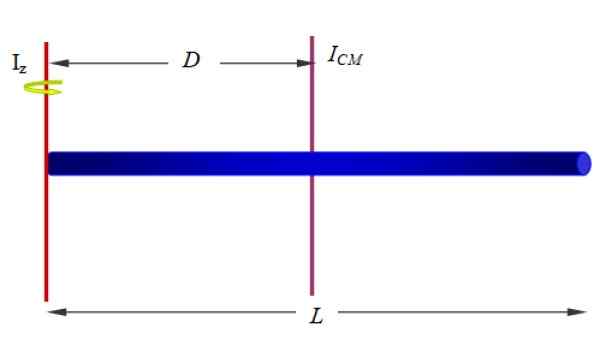Kuva 10. Homogeenisen baarin hitausmomentti akselin ympärillä, joka kulkee toisen pään läpi. Lähde: f. Zapata.

Ratkaisu:

Meillä on jo baarin hitaushetki akselin ympärillä, joka kulkee sen geometrisen keskuksen läpi. Koska baari on homogeeninen, sen massakeskus on siinä vaiheessa, joten tämä on meidän Yllyttää_Cm Steinerin lauseen soveltaminen.

Jos palkin pituus on Lens, Z -akseli on etäisyydellä D = l/2, siksi:

Yllyttää_{z -z} = I_Cm + MD²= (1/12) ml²+M (l/2)²= (1/3) ml²

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 313-340
2. Rex, a. 2011. Fysiikan perusteet. Pearson. 190-200.
3. Rinnakkaisakselin lause. Toipunut: Hyperfysiikka.Phy-Astr.GSU.Edu.
4. Serway, R. 2018. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Kyynärmä.
5. Sevillan yliopisto. Pallomaisten kiinteiden aineiden hitausmomentti. Toipunut: Laplace.meille.On.
6. Sevillan yliopisto. Hiukkasjärjestelmän hitausmomentti. Toipunut: Laplace.meille.On.
7. Wikipedia. Rinnakkaisakselin lause. Haettu: vuonna.Wikipedia.org