Montea Triplanar

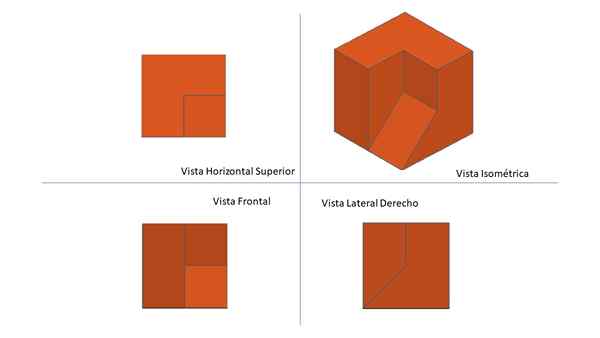
La Montea Triplanarissa kolmiulotteinen kappale on esitetty yhdellä tasolla, jossa ylemmän vaakasuoran näkymän ortogonaaliset projektiot, etunäkymä ja oikea profiilinäkymä asetetaan. Esitettyjen ennusteiden järjestys on ISO-A-standardin mukainen. Lähde: f. Zapata.

Mikä on kolminkertainen vuori?

Se Montea Triplanar Se on tapa edustaa tasossa olevaa kolmiulotteista hahmoa heidän kasvonsa ortogonaalisen projektion kautta Cartesian suunnitelmissa ja sijoitti kaikki projektiot yhteen tasoon.

Paras tapa ymmärtää projektiojärjestelmä on kuvitella luku läpinäkyvän materiaalin kuutioruudussa. Sitten kuvion kohtisuorat projektiot, läpinäkyvän laatikon jokaiselle pinnalle, viedään yhdelle tasolle.

La Montea Triplanissa kolme perusprojektiota viedään yhdelle tasolle, joka koostuu seuraavista näkymistä:

• Etu-.
• Vaakasuora.
• Oikea profiili.

Amerikkalaisen järjestelmän tapauksessa projektiotaso on tarkkailijan ja kuvan välillä, mutta eurooppalaisessa järjestelmässä projisointitaso on kuvan takana, havaintosuunnassa. 

Mikä on kolminkertainen vuori?

Kolminkertainen kiinnitys edustaa kolmiulotteisia hahmoja kahden dimensionaalisella pinnalla: taso, joka voi olla paperiarkki tai laitteen näyttö.

Tämä taso on jaettu neljään kvadranttiin, jotka on määritelty vaakasuorien ja pystysuorien akselien leikkauksella. 

Quadrantit on lueteltu seuraavasti:

• Ensimmäinen kvadrantti (i): Oikea yläosa kvadrantti.
• Toinen kvadrantti (II): vasen yläosa kvadrantti.
• Kolmas kvadrantti (III): vasen alakulmainen kvadrantti.
• Neljäs kvadrantti (IV): Oikea alaosa kvadrantti.

Voi palvella sinua: Korrelaatiokerroin: kaavat, laskenta, tulkinta, esimerkki

Amerikkalaisen järjestelmän (ISO-A-standardin) käytön tapauksessa projektiot sijaitsevat neljänneksissä seuraavan säännöksen mukaisesti:

1. Isometrisen projektion kolmen dimensioinen luku on ensimmäisessä kvadrantissa.
2. Toisessa kvadrantissa vaakasuuntainen näkymä asetetaan (kuvasta).
3. Frontaalitasossa olevan kuvan ortogonaalinen projektio sijaitsee kolmannessa kvadrantissa.
4. Lopuksi, neljännessä kvadrantissa oikea profiilinäkymä on sijoitettu, mikä on kuvan ja tarkkailijan välisen pystysuuntaisen kuvitteellisen tason projisointi oikeasta profiilista oikeasta profiilista.

Kolme edellä mainittua näkemystä ovat tarpeeksi, koska useimmissa tapauksissa on tarpeetonta sijoittaa muut, jotka ovat:

• Alempi vaakasuora.
• Vasen puoli.
• Takanäkymä.

Vain näitä näkemyksiä käytetään, jos mikä tahansa luku esitetään epäselvyyttä. Samoin tietyntyyppisissä kappaleissa on myös tarpeen asettaa näkymät niiden poikittaisesta tai pitkittäisleikkauksesta.

Montaa kolminkertaiset esimerkit

Esimerkki 1

Haluat rakentaa triplaarikiinnit, jotka vastaavat katkaistua kartiota, jonka pääakseli on yhdensuuntainen vaakatason kanssa, American ISO-A -standardin mukaan myös nimeltään Kolmas kulmaprojektio.

Koska se on katkaistu kartio, jonka symmetria -akseli on yhdensuuntainen vaakatason kanssa, pienempi halkaisijaltaan vastaava pinta -ala on eturintamassa.

Kone, johon kunkin näkymän oikeinkirjoitusprojektio sijoitetaan, jaetaan neljään kvadranttiin.

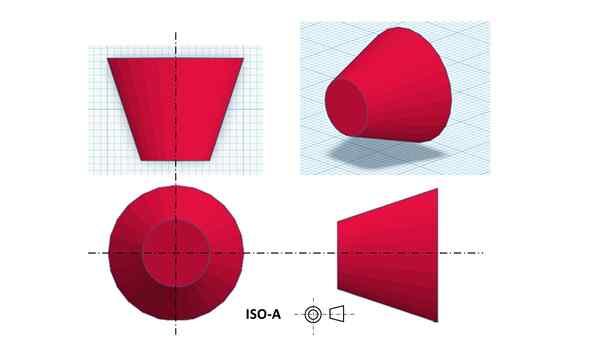Montaa triplanar de a truncado coin. Lähde: f. Zapata

Amerikkalaisessa järjestelmässä frontaalinen näkymä on sijoitettu kolmanteen kvadranttiin, minkä vuoksi tämä järjestelmä tunnetaan myös nimellä "kolmas kulma". 

Voi palvella sinua: Prosentuaalinen virhe

Vaakakuva ylhäältä on sijoitettu juuri etunäkymän yläpuolelle, toisin sanoen toisessa kvadrantissa.

Lopuksi, kuten amerikkalaisessa järjestelmässä, projektio pysyy tarkkailijan ja hahmon välillä, oikeanpuoleinen näkymä sijaitsee tarkalleen etunäkymän oikealla puolella, toisin sanoen neljännessä kvadrantissa.

Koska ensimmäinen kvadrantti oli vapaa, hahmon, tässä tapauksessa katkaistu kartio, on tarkalleen kolmen dimensioinen isometrinen näkymä.

Edellisessä luvussa voidaan nähdä myös yritys tai kuvake, joka vastaa amerikkalaista ISO-A-standardia, joka on kaksi samankeskistä ympyrää, joissa on tasa-arvoinen trapetsoidi oikealla puolella, joka on suunnattu siten, että lyhyt pohja on lähellä ympyröitä. Tämä harjoitus selittää vain tämän kuvakkeen syyn amerikkalaiselle normille.

Esimerkki 2

Triplaarikiinnityksen rakentaminen, joka vastaa katkaistua kartiota, jonka pääakseli on yhdensuuntainen vaakasuoran tason kanssa, eurooppalaisen standardin ISO-E: n mukaan, jota kutsutaan myös Ensimmäinen kulmaprojektio.

Tätä varten tehdään esimerkin 1 katkaistun kartion projektio, mutta tällä kertaa eurooppalaisella tai "ensimmäisen kulman" standardilla.

Samoin suunnitelma, johon kartion eri näkymät tai oikeinkirjoituksen projektiot asetetaan, se jaetaan neljään kvadranttiin.

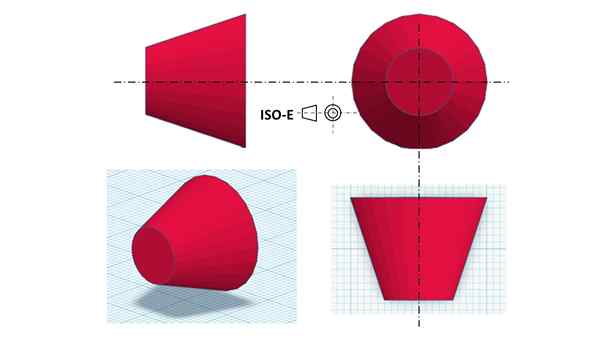Montaa triplanar de a truncado coin. Lähde: f. Zapata.

Ensimmäinen on tunnistaa etunäkymä, joka vastaa katkaistun kartion pienemmän halkaisijan pyöreää pintaa. Frontaalinen näkymä näyttää kahdelta samankeskiseltä ympyrästä: yksi sisempi, joka vastaa kartion pieninta pohjaa, ja toinen ulkopohjaa vastaava ulkopinta.

Voi palvella sinua: prismat ja pyramidit

Euroopan tai ”ensimmäisen kulman” yleissopimuksessa etunäkymä sijaitsee tarkalleen ensimmäisessä kvadrantissa.

Ylävaakasuora näkymä on sijoitettu etunäkymän alle, koska eurooppalaisessa järjestelmässä ortogonaalinen näköprojektio asetetaan kuvan taakse, havaintosuunnassa.

Tämä tarkoittaa, että ylempi näkymä on sijoitettu neljänteen kvadranttiin.

Olisi tarpeen löytää oikea sivukuva, joka eurooppalaisessa järjestelmässä sijaitsee etunäkymän vasemmalla puolella, toisessa kvadrantissa.

Koska kolmas kvadrantti on ollut vapaa, siellä on tapana sijoittaa kappaleen kolmen dimensioinen isometrinen projektio.

Tämä esimerkki oikeuttaa syyn Euroopan standardin sinetin, allekirjoituksen tai kuvakkeen syyn. Tämä koostuu kahdesta samankeskisestä ympyrästä, jotka edustavat katkaistujen kartioiden etunäkymää, sekä trapetsia, joka edustaa sitä oikeaa puolta, joka on asetettu ympyrän vasemmalle, pitkän pohjan vierekkäin.

Vuoristosovellukset

Kolminkertaista kiinnitystä sovelletaan kaikilla tieteenaloilla, joissa vaaditaan asteikon esitys paperilla tai taulutuotteilla.

Tästä syystä tämä esitysmuoto, joka on osa kuvaavaa geometriaa, on tutkimuksen asia aloilla, kuten:

• Mekaaninen suunnittelu.
• Metalmekaaniset rakenteet.
• rakennustekniikka.
• Terveystilojen piirtäminen.
• Arkkitehtoninen suunnittelu.
• Kaupunkisuunnittelu.
• Topografia.

Tästä syystä La Montea Triplan on pakollinen tutkimus teknisissä kouluissa ja arkkitehtuurin ja tekniikan uralla osana aiheet, kuten kuvaava geometria tai projektiivinen geometria. 

Vertailu kirjallisuuden ja kirjallisuuden tutkimuksiin, joissa kielioppi on perusta ideoiden ja tunteiden välittämiselle, projekti geometria on perustavanlaatuista tekniikassa ja arkkitehtuurissa. Sen ansiosta on mahdollista ymmärtää, tulkita ja ottaa ideoita suunnitelmista käytännön toteuttamiseen.