Suorakulmaiset liikkeen ominaisuudet, tyypit ja esimerkit

Hän peräsuolen liike Se on sellainen, jossa matkapuhelin liikkuu suoraa linjaa pitkin ja ohittaa siten ulottuvuuden, joten myös vastaanottaa nimen Yksidimensionaalinen liike. Tämä suora linja on suunta tai polku, jota seuraa liikkuva esine. Kuvan 1 katata pitkin kulkevat autot seuraavat tämän tyyppistä liikettä.

Tämä on yksinkertaisin liikkumismalli, joka voidaan kuvitella. Ihmisten, eläinten ja asioiden päivittäiset liikkeet yhdistävät usein siirrot suorassa linjassa käyrien varrella olevien liikkeiden kanssa, mutta jotkut usein tarkkailevat joitain, jotka ovat yksinomaan suoraviivaista.

Kuvio 1. Autot, jotka liikkuvat suorakulmaisen kadun varrella. Lähde: Pixabay.

Tässä on hyviä esimerkkejä:

- Kun juoksut 200 metrin suoraviivaisen radan varrella.

- Auton ajaminen suoralla tiellä.

- Objektin pudottaminen tietystä korkeudesta.

- Kun pallo heitetään pystysuoraan.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Nyt liikettä kuvata tavoite saavutetaan määrittelemällä ominaisuudet, kuten:

- Sijainti

- Siirtymä

- Nopeus

- Kiihtyvyys

- Aika.

Jotta tarkkailija voidaan havaita objektin liikkeen, on välttämätöntä olla vertailupiste (alkuperä O) ja on luonut tietyn osoitteen liikkua, joka voi olla akseli x, akseli ja tai mikä tahansa muu.

Mitä tulee liikkumaan, tällä voi olla lukemattomia tapoja. Tässä suhteessa ei ole rajoituksia, mutta kaikessa, joka seuraa sitä, oletetaan, että matkapuhelin on hiukkas; esine niin pieni, että sen mitat eivät ole merkityksellisiä.

On tiedossa, että näin ei ole makroskooppisten esineiden suhteen; Se on kuitenkin malli, jolla on hyviä tuloksia esineen globaalin liikkeen kuvauksessa. Tällä tavoin hiukkas voi olla auto, planeetta, henkilö tai mikä tahansa muu liikkuva esine.

Aloitamme tutkimuksemme suoraviivaisesta kinematiikasta yleisellä lähestymistavalla liikkeeseen, ja sitten tiettyjä tapauksia tutkitaan, kuten jo nimitetyt.

[TOC]

Strektilinoisen liikkeen yleiset ominaisuudet

Seuraava kuvaus on yleinen ja sovellettava minkä tahansa tyyppiseen yhden dimensioiseen liikkeeseen. Ensimmäinen asia on valita referenssijärjestelmä. Linja, jota pitkin liike tapahtuu, on akseli x. Liikkeen parametrit:

Sijainti

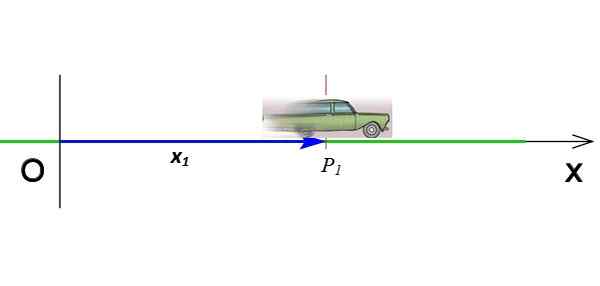Kuva 2. X -akselilla liikkuvan matkapuhelimen sijainti. Lähde: Wikimedia Commons (muokattu F. Zapata).

Se on vektori, joka siirtyy alkuperästä siihen pisteeseen, jossa esine on hetkessä. Kuviossa 2 vektori x₁ Osoittaa matkapuhelimen sijainnin, kun se on koordinaatissa P₁ ja ajoissa t₁. Kansainvälisen järjestelmän sijaintivektoriyksiköt ovat metri.

Siirtymä

Siirtymä on vektori, joka osoittaa aseman muutoksen. Kuviossa 3 auto on mennyt asennosta P₁ asemaan P₂, Siksi sen siirtymä on δx = x₂ - x₁. Siirtymä on kahden vektorin vähentäminen, se symboloidaan kreikkalaisella kirjaimella δ ("delta") ja on puolestaan ​​vektori. Sen yksiköt kansainvälisessä järjestelmässä ovat metri.

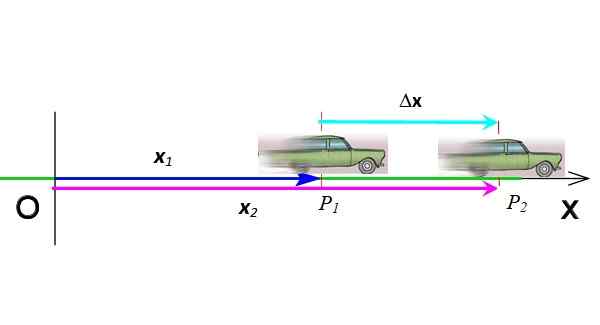Kuva 3. Vektorin siirtymä. Lähde: valmistettu f. Zapata.

Vektorit on merkitty lihavoituna painetussa tekstissä. Mutta ollessasi samassa ulottuvuudessa, voit halutessasi tehdä ilman vektorimerkintää.

Voi palvella sinua: klassisen ja modernin fysiikan haarat

Matkan matka

Etäisyys d -d Liikkuvan esineen kiertämä on siirtymävektorin absoluuttinen arvo:

D = ΙxΙ = δx

Absoluuttinen arvo, kuljetettu etäisyys on aina suurempi tai yhtä suuri kuin 0 ja sen yksiköt ovat samat kuin sijainnin ja siirtymisen alueet. Absoluuttinen arvomerkinnät voidaan tehdä moduulipalkeilla tai yksinkertaisesti poistamalla lihavoitu kirjain painetussa tekstissä.

Keskinopeus

Kuinka nopeasti sijainti muuttuu? Siellä on hitaita ja nopeita matkapuhelimia. Avain on aina ollut nopeus. Tämän tekijän analysoimiseksi sijainti analysoidaan x ajan funktio t.

Keskimääräinen nopeus v_m (Katso kuva 4) Se käyrän kuivausviivan (fuksia) kaltevuus x vs t ja tarjoaa globaalia tietoa mobiililaitteiden siirrosta tarkasteltavana aikavälillä.

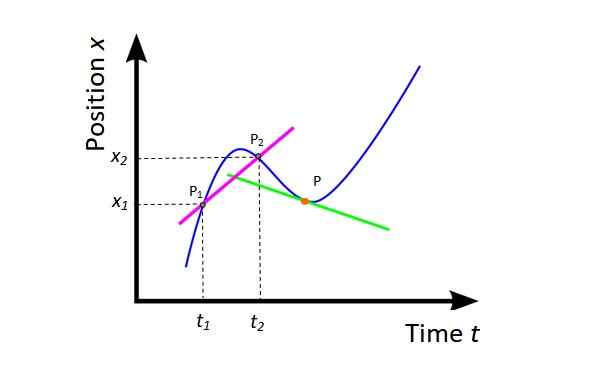Kuva 4. Keskimääräinen nopeus ja hetkellinen nopeus. Lähde: Wikimedia Commons, muokattu F. Zapata.

v_m = (x₂ - x₁) / (t₂ -t₁) = Δx / Δt

Keskimääräinen nopeus on vektori, jonka yksiköt kansainvälisessä järjestelmässä ovat Metriä /toinen (neiti-A.

Välitön nopeus

Keskimääräinen nopeus lasketaan ottamalla mitattavissa oleva aikaväli, mutta ei ilmoiteta siitä, mitä tapahtuu mainitulla aikavälillä. Jotta nopeus tietää milloin tahansa, sinun on tehtävä aikaväli hyvin pieni, matemaattisesti se vastaa:

Δt → 0 -

Yhtälö annetaan aikaisemmin keskimääräisen nopeuden suhteen. Tällä tavoin saadaan hetkellinen nopeus tai yksinkertaisesti nopeus:

Geometrisesti aseman johdannainen ajan suhteen on käyrän tangentin kaltevuus x vs t tietyssä vaiheessa. Kuviossa 4 kohta on oranssi ja tangenttiviiva on vihreä. Hetkellinen nopeus tässä vaiheessa on tuon viivan kaltevuus.

Nopeus

Nopeus määritellään absoluuttiseksi arvoksi tai nopeusmoduuliksi ja on aina positiivinen (signalointi, tiet ja moottoritiet ovat aina positiivisia, eivät koskaan negatiivisia). Termejä "nopeus" ja "nopeus" voidaan käyttää päivittäin, mutta fysiikassa vektorin ja kiipeilyn välinen ero on välttämätöntä.

v = ΙvΙ = v

Keskimääräinen kiihtyvyys ja välitön kiihtyvyys

Nopeus voi muuttua liikkeen aikana ja todellisuus on, että sen odotetaan tekevän niin. On olemassa suuruus, joka määrittelee tämän muutoksen: kiihtyvyys. Jos huomaamme, että nopeus on aseman muutos ajan suhteen, kiihtyvyys on nopeuden muutos ajan suhteen.

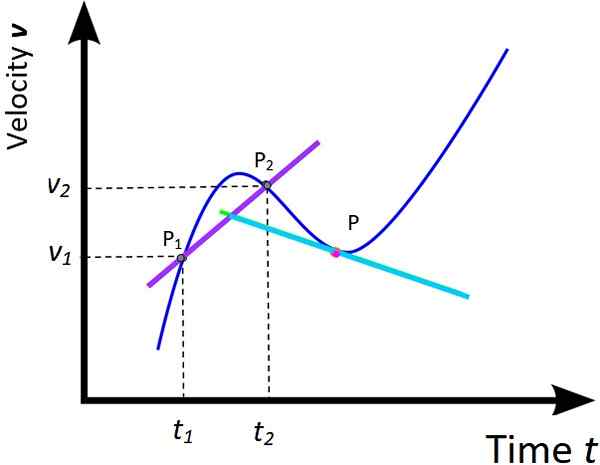Kuva 5. Keskimääräinen kiihtyvyys ja välitön kiihtyvyys. Lähde: Wikimedia Commons, muokattu F. Zapata.

Käsittely x vs t kahdesta edellisestä osasta voidaan laajentaa vastaavaan kaavioon v vs t. Näin ollen keskimääräinen kiihtyvyys ja välitön kiihtyvyys määritellään seuraavasti:

-lla_m = (v₂ - v₁) / (t₂ -t₁) = Δv / Δt  (Odotettaessa asuinpaikkaa)

Kiihtyvyys

Yhden ulottuvuuden liikkeessä vektoreilla valmistelukunnan mukaan ovat positiivisia tai negatiivisia merkkejä, kun ne menevät tavalla tai toisella. Kun kiihtyvyydellä on sama merkitys kuin nopeudella, se lisää sen suuruutta, mutta kun se on päinvastainen ja nopeus vähentää sen suuruutta. Sitten sanotaan, että liike viivästyy.

Voi palvella sinua: Leyden -pullo: Osat, toiminta, kokeet

Kaverit

Strektililaisten liikkeiden luokittelu tehdään yleensä:

- Onko kiihtyvyys vakiona.

- Liike kulkee vaakasuoraa tai pystysuoraa viivaa pitkin.

Liikkuminen jatkuvalla kiihtyvyydellä

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Kun kiihtyvyys on vakio, keskimääräinen kiihtyvyys -lla_m Se on yhtä suuri kuin välitön kiihtyvyys -lla Ja vaihtoehtoja on kaksi:

- Että kiihtyvyyden arvo on 0, jolloin nopeus on vakio ja sillä on tasainen suorakulmainen liike tai MRU.

- Jatkuva kiihtyvyys, joka eroaa 0: sta, jossa nopeus kasvaa tai vähenee lineaarisesti ajan myötä (suoraviivainen liike tasaisesti vaihteli tai MRUV):

Missä v_F  ja t_F Ne ovat vastaavasti lopullinen nopeus ja aika, ja v_jompikumpi ja t_jompikumpi Ne ovat alustavan nopeuden ja aikaa. Joo t_jompikumpi = 0, Kun puhdistat lopullisen nopeuden, sinulla on jo tuttu lopullista nopeutta varten:

v_F = v_jompikumpi + At

Tätä liikettä varten seuraavat yhtälöt ovat myös voimassa:

- Sijainti ajasta riippuen: x = x_jompikumpi + v_{jompikumpi .}t +½²

- Nopeus sijainnista riippuen: v_F² = v_jompikumpi² + Toinen.Δx  (Δ: n kanssax = x - x_jompikumpi-A

Vaakasuorat liikkeet ja pystysuorat liikkeet

Vaaka -alueet ovat ne, jotka kulkevat vaakasuoraa akselia tai x -akselia pitkin, kun taas pystysuorat tekevät sen akselia ja akselia pitkin. Pystysuorat liikkeet painovoiman alla ovat yleisimmät ja mielenkiintoisimmat.

Edellisissä yhtälöissä se otetaan A = g = 9.8 m/s² Pystysuoraan suunnattu suunta, joka on melkein aina valittu negatiivisella merkinnällä.

Tällä tavalla, v_F = v_jompikumpi + At Se muuttuu v_F = v_jompikumpi - GT Ja jos alkuperäinen nopeus on 0, koska esine pudotettiin vapaasti, sitä yksinkertaistetaan edelleen v_F = - GT. Niin kauan kuin ilmankestävyyttä ei tietenkään oteta huomioon.

Ratkaistu esimerkki

Esimerkki 1

Kohdassa A pieni paketti vapautetaan siten, että se liikkuu kuljettajaa pitkin liukupyörillä ABCD, joka on esitetty kuvassa. Vaikka paketti laskeutuu kaltevien osien AB ja CD -levyjen läpi, se on kiihtyvyys 4,8 m/s², kun taas vaakasuorassa osassa BC ylläpitää jatkuvaa nopeutta.

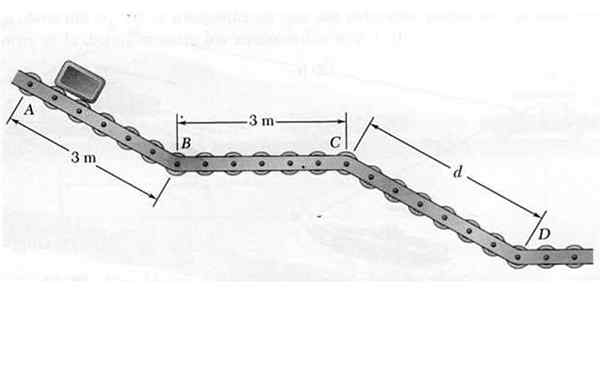Kuva 6. Paketti, joka liikkuu ratkaistun esimerkin 1 liukupolulla. Lähde: Itse tehty.

Tietäen, että nopeus, jolla paketti D on saavuttaa, on 7,2 m/s, määritä:

a) C: n ja D: n välinen etäisyys.

b) Paketin tarvittava aika päättymiseen.

Ratkaisu

Pakkauksen liikkuminen suoritetaan kolmessa esitetyssä suorakulmaisessa osassa, ja pyydettyjen laskemiseksi nopeus vaaditaan kohdissa B, C ja D. Analysoidaan jokainen osa erikseen:

Osa AB

Koska aikaa ei ole saatavana tässä osiossa, sitä käytetään v_F² = v_jompikumpi² + Toinen.Δx  VO = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → v_F  = 5.37 m/s = V_{B -}

Aika, jonka paketti kulkee osion AB: n matkustamiseen, on:

t_Ab = (v_F - v_jompikumpi) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Osa bc

Siis nopeus osassa BC on vakio, siksi v_{B -} = v_C = 5.37 m/s. Aika, jonka paketti kuluu tämän osan matkustamiseen, on:

Voi palvella sinua: kevyt taittuminen: elementit, lait ja kokeilu

t_BC = etäisyys _BC  / v_{B -} = 3 m/ 5.37 m/s = 0.56 s

CD -osa

Tämän osan alkuperäinen nopeus on v_C = 5.37 m/s, Viimeinen nopeus on v_{D -d} = 7,2 m/s, kautta v_{D -d}²  = v_C² + 2. -lla. d -d Arvo d -d-

D = (v_{D -d}²  - v_C²)/2.A = (7.2²  - 5.37²)/2 x 4.8 m = 2.4 m

Aika lasketaan seuraavasti:

t_{CD =} (V_{D -d}  - v_C)/A = (7,2- 5.37)/ 4.8 s = 0.38 s.

Esitettyihin kysymyksiin vastaukset ovat:

a) d = 2.4 m

b) matka -aika on t_Ab + t_BC + t_CD = 1.19 s +0.56 s +0.38 s = 2.13 s.

Esimerkki 2

Henkilö on vaakasuoran portin alla, joka on alun perin avoin ja 12 m korkea. Henkilö käynnistää objektin pystysuunnassa kohti porttia 15 m/s nopeudella.

On tiedossa, että portti sulkeutuu 1,5 sekuntia sen jälkeen, kun henkilö on käynnistänyt esineen 2 metrin korkeudesta. Ilmankestävyyttä ei oteta huomioon. Vastaa seuraaviin kysymyksiin perustelemalla:

a) onnistutko siirtämään objektin portin läpi ennen kuin se sulkeutuu?

b) törmääkö esine koskaan suljettua porttia vasten? Jos se myöntää, milloin se tapahtuu?

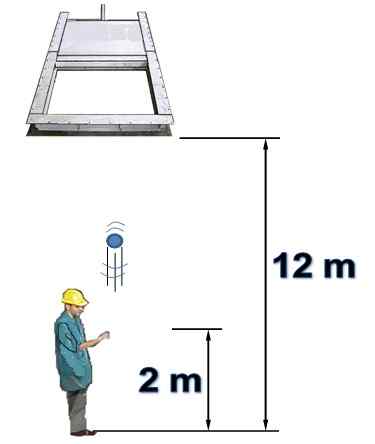Kuva 7. Objekti käynnistetään pystysuoraan (ratkaistu esimerkki 2). Lähde: Itse tehty.

Vastaa)

Pallon ja portin alkuasennon välillä on 10 metriä. Se on pystysuora käynnistys ylöspäin, jossa tätä osoitetta pidetään positiivisena.

Voit selvittää sen nopeuden, jonka se kuljettaa, kun saavut tähän vaiheeseen, tällä tuloksella sen tekeminen kului ja vertaa sitä portin sulkemisaikaan, joka on 1.5 sekuntia:

v_F ²= v_jompikumpi ²- 2.g. Δja → v_F = (15² - 2 x 9.8 x10)^1/2 M = 5.39 m/s

T = (v_F - v_jompikumpi) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Koska tämä aika on alle 1.5 sekuntia, sitten päätellään, että esine voi mennä portin läpi ainakin kerran.

Vastaus b)

Tiedämme jo, että esine hallitsee. Nopeudella, kun se nousee portin korkeuteen, on sama suuruus kuin kun se nousee, mutta vastakkaiseen suuntaan. Siksi työskentele -5: n kanssa.39 m/s ja tämän tilanteen saavuttamiseen tarvittava aika on:

T = (v_F - v_jompikumpi) /G = (-5.39 - 15) / (-9.8) s = 2.08 s

Koska portti pysyy auki vain yhdellä.5 s, on selvää, että sillä ei ole aikaa kulkea ennen kuin se sulkeutuu, koska se on suljettu. Vastaus on: esine, jos se törmää suljetun portin kanssa 2 jälkeen.08 sekuntia julkaisun jälkeen, kun se tulee laskeutumaan.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).69-116.
2. Giancoli, D. Fysiikka. (2006). Periaatteet hakemuksissa. 6^th Painos. Prentice Hall. 22-25.
3. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 23 - 27.
4. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 21-22.
5. Rex, a. (2011). Fysiikan perusteet. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Osa 1. 50 - 53.
7. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 7^mehu. Painos. Meksiko. Cengage Learning Editors. 23-25.
8. Serway, R., ULOLE, c. (2011). Fysiikan perusteet. 9^naa Ed. Cengage -oppiminen. 43 - 55.
9. Wilson, J. (2011). Fysiikka 10. Pearson -koulutus. 133 - 149.