Gauss-Seidel-menetelmän selitys, sovellukset, esimerkit

Hän Gauss-Seidel-menetelmä Se on iteratiivinen menettely löytää likimääräisiä ratkaisuja lineaaristen algebrallisten yhtälöiden järjestelmään mielivaltaisesti valitulla tarkkuudella. Menetelmä koskee neliömatriiseja, joissa ei ole nolla -elementtejä sen diagonaaleissa ja lähentyminen taataan, jos matriisi on diagonaalisesti hallitseva.

Sen on luonut Carl Friedrich Gauss (1777-1855), joka teki yksityisen mielenosoituksen yhdelle hänen opiskelijoistaan ​​vuonna 1823. Myöhemmin sen virallisesti julkaisi Philipp Ludwig von Seidel (1821-1896) vuonna 1874, joten molempien matemaatikkojen nimi.

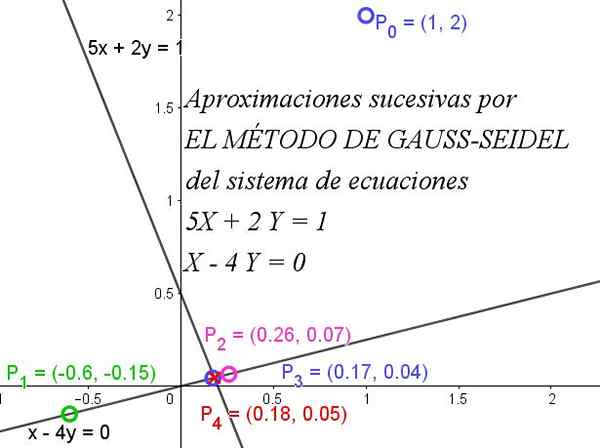
Kuvio 1. Gauss-Seidelin menetelmä lähentyy nopeasti yhtälöjärjestelmän hankkimiseksi. Lähde: f. Zapata.

Menetelmän täydellisen ymmärtämisen kannalta on tarpeen tietää, että matriisi on diagonaalisesti hallitseva, kun kunkin rivin diagonaalielementin absoluuttinen arvo on suurempi tai yhtä suuri kuin muiden elementtien absoluuttisten arvojen summa samasta rivistä.

Matemaattisesti se ilmaistaan ​​seuraavasti:

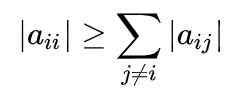
[TOC]

Selitys yksinkertaisen tapauksen kautta

Havainnollistaaksesi, mitä Gauss-Seidel-menetelmä ottaa yksinkertaisen tapauksen, josta löydät X: n ja Y: n arvot alla esitetyssä 2 × 2 lineaarisessa yhtälöjärjestelmässä:

5x + 2y = 1

X - 4y = 0

Seuraavat vaiheet

1- Ensinnäkin sinun on määritettävä, onko lähentyminen turvallista. Heti havaitaan, että käytännössä se on diagonaalisesti hallitseva järjestelmä, koska ensimmäisellä rivillä ensimmäisellä kertoimella on suurempi absoluuttinen arvo kuin eturivin muilla:

| 5 |> | 2 |

Samoin toisen rivin toinen kerroin on myös diagonaalisesti hallitseva:

| -4 |> | 1 |

2- Muuttujat x ja y ovat selkeitä: 

X = (1 - 2y)/5

Y = x/4

3- Alkuperäinen mielivaltainen arvo sijoitetaan, nimeltään “siemen”: xo = 1, ME = 2.

4

Se voi palvella sinua: arviointia välein

X1 = (1 - 2 Me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- jatka samalla tavalla saadaksesi yhtälöjärjestelmän liuoksen toinen lähentäminen:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Kolmas iteraatio:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- neljäs iteraatio, tämän havainnollistavan tapauksen lopullisena iteraationa:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Nämä arvot osuvat melko hyvin muiden resoluutiomenetelmien avulla löydetyn liuoksen kanssa. Lukija voi tarkistaa sen nopeasti online -matemaattisen ohjelman avulla.

Menetelmäanalyysi

Kuten voidaan nähdä, Gauss-Seidel-menetelmässä edelliselle muuttujalle samassa vaiheessa saadut likimääräiset arvot on korvattava seuraavassa muuttujassa. Tämä erottaa sen muista iteratiivisista menetelmistä, kuten Jacobi, jossa kukin vaihe vaatii lähestymistavat edelliseen vaiheeseen. 

Gauss-Seidelin menetelmä ei ole rinnakkainen menettely, kun taas Gauss-Jordan on. Se on myös syy siihen, että Gauss-Seidel-menetelmällä on nopeampi lähentymisvapaa askel-Jordanin menetelmä.

Mitä tulee diagonaalisesti hallitsevaan matriisi -olosuhteeseen, tämä ei aina ole tyytyväinen. Useimmissa tapauksissa riittää kuitenkin vaihtamaan alkuperäisen järjestelmän joukkoja ehdon täyttämiseksi. Lisäksi menetelmä lähentyy melkein aina, vaikka diagonaalista määräävää olosuhteita ei täytetä.

Aikaisempi tulos, joka saadaan Gauss-Seidel-menetelmän neljällä iteraatiolla, voidaan kirjoittaa desimaalilla:

Voi palvella sinua: kuinka monta symmetria -akselia ympyrällä on?

X4 = 0,1826

Y4 = 0,04565

Tarkka ratkaisu nostettuun yhtälöjärjestelmään on:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Joten vain 4 iteraatiolla tulos saadaan tuhanneksi tarkkuudella (0,001).

Kuvio 1 kuvaa kuinka peräkkäiset iteraatiot lähentyvät nopeasti tarkkaan ratkaisuun.

Sovellukset

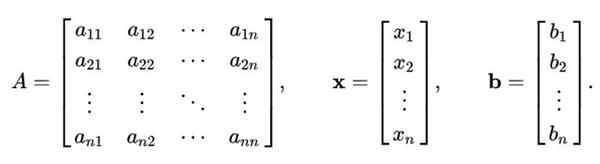
Gauss-Seidel-menetelmä ei ole rajoitettu vain 2 × 2 lineaariseen yhtälöjärjestelmään. Yllä oleva menettely voidaan yleistää lineaarisen järjestelmän ratkaisemiseksi n yhtälöt jhk n Tuntemattomat, jotka ovat edustettuina matriisien tyyppisiä:

-Lla X = b -

Missä -Lla Se on matriisi n x n, sillä aikaa X Se on laskettavien muuttujien vektori N -komponentit; ja b - Se on vektori, joka sisältää riippumattomien termien arvot.

Havainnollistavassa tapauksessa käytettyjen iteraatioiden sekvenssin yleistämiseksi N X N -järjestelmään, joka haluaa laskea muuttujan Xi, Seuraava kaava sovelletaan:

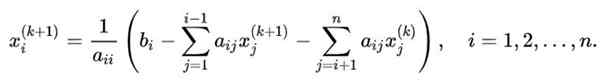
Tässä yhtälössä:

- k -k - Se on iteraatiossa saadun arvon indeksi k -k -.

-K+1 Osoittaa uuden arvon seuraavassa.

Iteraatioiden lopullinen lukumäärä määritetään, kun iteraatiossa saatu arvo K+1 eroaa välittömästi aikaisemmin saatuun määrään ε, joka on juuri haluttu tarkkuus.

Esimerkkejä Gauss-Seidel-menetelmästä

- Esimerkki 1

Kirjoita yleinen algoritmi, jonka avulla voit laskea likimääräisen ratkaisuvektorin X NXN -yhtälöiden lineaarisesta järjestelmästä, kertoimen matriisin perusteella -Lla, Riippumattomien ehtojen vektori b -, Iteraatioiden lukumäärä (iter) ja vektorin alku- tai "siemen" X.

Ratkaisu

Algoritmi koostuu kahdesta "syklistä", toinen iteraatioiden lukumäärästä ja toinen muuttujien lukumäärästä. Se olisi seuraava:

K ∊ [1 ... iter]

I ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Voi palvella sinua: desimaalimerkinnät

- Esimerkki 2

Tarkista edellisen algoritmin toiminta soveltamalla matemaattisia ohjelmistoja SMATH -Studio Ilmainen ja ilmainen, saatavana Windowsille ja Androidille. Ole esimerkki esimerkiksi 2 × 2-matriisin tapauksesta, joka palveli meitä havainnollistamaan Gauss-Seidel-menetelmää.

Ratkaisu

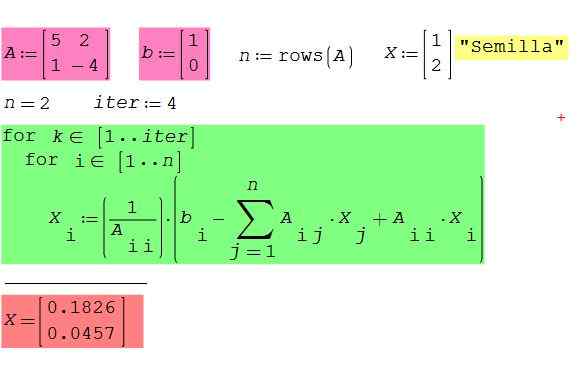Kuva 2. Esimerkkiyhtälöjärjestelmä 2 x 2, käyttämällä ohjelmistoa SMATH -Studio. Lähde: f. Zapata.

- Esimerkki 3

Levitä Gauss-Seidel-algoritmia seuraaville 3 × 3 -yhtälöjärjestelmälle, joka on aiemmin tilattu siten, että diagonaalikertoimet ovat hallitsevia (toisin sanoen suurempi absoluuttinen arvo kuin kertoimien kertoimien absoluuttisilla arvoilla saman rivin):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Käytä NULL -vektoria siemeninä ja harkitse viittä iteraatiota. Kommentoi tulosta.

Ratkaisu

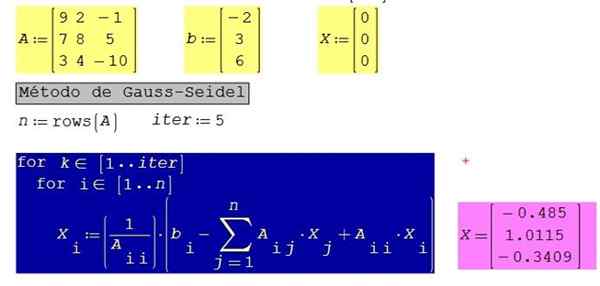Kuva 3. Ratkaistun esimerkin 3 yhtälöjärjestelmän ratkaisu, käyttämällä SMATH Studio. Lähde: f. Zapata.

Samassa järjestelmässä, jossa on 10 iteraatiota 5: n sijasta, saadaan seuraavat tulokset: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Tämä osoittaa, että se riittää viidellä iteraatiolla saadaksesi kolme tarkkuutta desimaalia ja että menetelmä välittää nopeasti liuokseen.

- Esimerkki 4

Löydä Gauss-Seidel-algoritmin avulla alla tapahtuvan 4 × 4 -yhtälöjärjestelmän ratkaisu:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Menetelmän aloittamiseksi hyödyntämällä tätä siemeniä:

x1 = 0, x2 = 0, x3 = 0 ja x4 = 0

Harkitse 10 iteraatiota ja arvioi tuloksen virhettä verrattuna iteraatioon 11.

Ratkaisu

Kuva 4. Ratkaistun esimerkin 4 yhtälöjärjestelmän ratkaisu, käyttämällä SMATH Studio. Lähde: f. Zapata.

Kun verrataan seuraavaan iteraatioon (numero 11), tulos on identtinen. Suurimmat erot kahden iteraation välillä ovat luokkaa 2 × 10^-8, Mikä tarkoittaa, että esitetyn ratkaisun tarkkuus on vähintään seitsemän desimaalia.

Viitteet

1. Iteratiiviset ratkaisumenetelmät. Gauss-Seidel. Toipunut: cimat.MX
2. Numeeriset menetelmät. Gauss-Seidel. Palautettu: testi.CUA.Ura.MX
3. Numeerinen: Gauss-Seidel-menetelmä. Toipunut: Opi lineassa.sinä.Edu.yhteistyö
4. Wikipedia. Gauss-Seidel-menetelmä. Haettu: vuonna. Wikipedia.com
5. Wikipedia. Gauss-Seidel-menetelmä. Palautettu: on.Wikipedia.com