Kaksoisnäytteenotto

Selitämme, mikä on kaksinkertainen näytteenotto, esimerkit, edut ja haitat ja laitamme ratkaisut harjoitukset

Kaksinkertaisessa näytteessä haluat tietää syvemmin populaation muuttujan

Mikä on kaksinkertainen näytteenotto?

Hän Kaksoisnäytteenotto Se on tekniikka, jota käytetään päätelmätilastoissa, kun haluat tietää yksityiskohtia ja varmuutta tietystä muuttujasta, joka on ominainen tietylle väestölle.

Toinen populaationäyte suoritetaan yleensä ensimmäisen näytteen jälkeen, jonka analyysi ei osoittanut tilastollisesti merkitsevää johtopäätöstä mistä tahansa tutkimusmuuttujasta ja analysoitiin.

Tästä syystä kaksoistilastot ovat myös tunnetuina nimellä Kaksi vaihetta näytteenotto. Toisen näytteen hyödyllisyys on, jossa se auttaa määrittämään tarkemmin tietyn apumuuttujan syiden ja regressioiden arvioinnin, joka syntyy ensimmäisen näytteen analyysin valossa.

Toinen kaksinkertaiseen näytteenottoon annettava käyttö on kerätä tietoja kerrosten näytteenoton toteuttamiseksi.

Esimerkit

Alla on erilaisia ​​tilanteita, joissa kaksinkertainen näytteenotto on perusteltua.

Laadunvalvonta kappaleiden kehittämisessä

Kaksinkertaista näytteenottomenetelmää käytetään usein teollisuuden laadunvalvonnassa ja se tehdään yleensä kahdessa vaiheessa.

Oletetaan esimerkiksi teollisuuskone, joka valmistaa tiettyjä kappaleita. Niin paljon kuin kone on säädetty, mikään pala ei ole identtinen toisen kanssa, koska sen mittoissa ja painossa voi tapahtua pieniä variaatioita. Kyse on sen määrittämisestä, täyttävätkö paljon mainitun koneen valmistamia osia toleranssikriteerejä siten, että se hyväksytään tai hylätään.

Ensinnäkin otetaan satunnainen näyte kappaleista, joilla yksi muuttujista on tarkistettava, esimerkiksi kappaleen pituus on toleranssin sisällä.

Jos keskimääräinen pituus on halutun toleranssiasteen alapuolella tai sen yläpuolella, tässä ensimmäisessä näytteessä päätellään, että erä on viallinen ja se on hylättävä. Tässä tapauksessa ei tarvitse ottaa uusia näytteitä.

Voi palvella sinua: Korrelaatiokerroin: kaavat, laskenta, tulkinta, esimerkki

Päinvastoin, jos keskiarvo on toleranssialueella, mutta näytteen keskihajonta on riittävän suuri summan tai vähentämisen keskimääräiseen arvoon on marginaalin ulkopuolella, niin on tarpeen kerätä toinen päänäyte.

Tämän toisen näytteen on sisällytettävä alkuperäinen näyte laskelmien uudelleenmuotoimiseksi ja siten voidakseen tehdä lopullisen päätöksen tutkitusta muuttujasta. Tällä tavalla voidaan tietää, onko erä viallinen vai ei.

Näytteenottokustannusten lasku

Monissa tapauksissa tietoa yhdestä tutkimuksesta, jota haluat opiskella. Mutta tiedonkeruua varten voi olla apumuuttuja helpommin.

Tässä tapauksessa otetaan kaksi näytettä, suuri apumuuttujalle, halvemmalle ja pieni näyte, joka sisältyy kalleimman muuttujan tärkeimpaan näytteeseen.

Tätä menetelmää voidaan soveltaa aina, kun määritetään, että molempien muuttujien välillä on korrelaatio, mikä on yleensä suhteellisuussuhde.

Esimerkki tästä tilanteesta esiintyy metsätieteissä, joissa halutaan määrittää loiskasvin (La Tiña) vaikuttavien puiden prosenttiosuus (La Tiña).

Koska nämä ovat erittäin laajoja ja vaikeita pääsyalueita, puiden täydellinen väestö on mahdotonta ajankohtana ja kustannuksissa. Näitä vaiheita noudatetaan sitten:

Vaihe 1: Näytteenotto

Alustava näytteenotto koostuisi ilmavalokuvan käytöstä ja metsä jaetaan eriksi. Muutama erä valitaan satunnaisesti ja arvioidaan analysoimalla valittujen erien kuvat, kuinka moniin puihin soittomato vaikuttaa, koska puiden väri vaikuttaa loinen.

Voi palvella sinua: Euclid -lause

Vaihe 2: Kenttätyö

Mutta valokuvausanalyysi ei voi olla tarkka, joten valitsemme mieluiten satunnaisesti muutamia ensimmäisiä näytteitä kenttätyön tekemiseksi.

Vaihe 3: Vertailu

Sitten kenttätulosta verrataan valokuvaan kahden erän sieppaamisen suhteen. Tämä vertailu voidaan suorittaa esimerkiksi kuvaajan valmistuksessa, jossa vaaka -akseli on jokaiselle erälle saatu arvo valokuvauksen avulla ja pystysuuntaisella akselilla, joka on saatu erällä kenttätyön kautta.

Tämä graafinen menetelmä mahdollistaa visuaalisesti tunnistamisen, onko kahden tuloksen välillä korrelaatio ja määritetty regressioanalyysi, suhteellisuus tai suhdekerroin kahden näytteen välillä.

Suurimman näytteen jälkeen, toisin sanoen valokuvanäyte, tartunnan saaneiden puiden keskiarvo ja sen keskihajonta otetaan. Mutta kun suhteellisuuskerroin ja sen virhe kenttänäytteillä määritettiin, on mahdollista korjata päänäytteen tulos (valokuva).

Sitten tämä tulos voidaan ekstrapoloida koko puiden väestöön.

Kaksinkertaisen näytteenoton edut ja haitat

Kuvatuissa esimerkeissä kustannusetu on todiste.

Haittana on, että kaksinkertaisen näytteenoton laadunvalvonnan suhteen on riski käydä läpi paljon tuotteita, jotka ovat suvaitsevaisuuden ulkopuolella.

Harjoittele

Haluat arvioida sairaiden puiden lukumäärän 162 hehtaarin metsässä. Koska metsä on erittäin laaja, se on jaettu samasta alueesta 100 tonttiin. 18 kuvaajaa valitaan satunnaisesti ja valokuvatutkimuksen avulla niiden arvioidaan, että näissä 18 kuvaajassa on 8 sairaspuun, joiden vakiovirhe on noin 4,5 puuta.

Voi palvella sinua: mitkä ovat osan osia? (Esimerkkejä)

Näistä 18 kuvaajasta 8 kuvaajaa valitaan satunnaisesti. Näille kahdeksalle kuvaajalle valokuvatutkimus johtaa 10 sairaspuun, joiden virhe on enemmän tai vähemmän 5,3 puuta.

Toisaalta, samoille kahdeksalle kuvaajalle kenttätutkimus heittää 12,4 sairas puita, joiden virhe on yli 6,3 puuta.

Sitä pyydetään:

• a) Määritä kenttätutkimuksen välinen suhteellisuuskerroin lineaarisella regressiolla.
• b) Arvioi sairaiden puiden lukumäärä sadan kuvaajan valokuvausmenetelmän avulla.
• c) Sovelletaan korjaus saadun suhteellisuuskertoimen kanssa, jotta voidaan arvioida sairaiden puiden todellisen lukumäärän koko metsässä.

Ratkaisu

Kaavio puiden lukumäärästä valokuvan lukumäärää verrattuna molemmille tutkimuksille valituille kahdeksalle erälle.

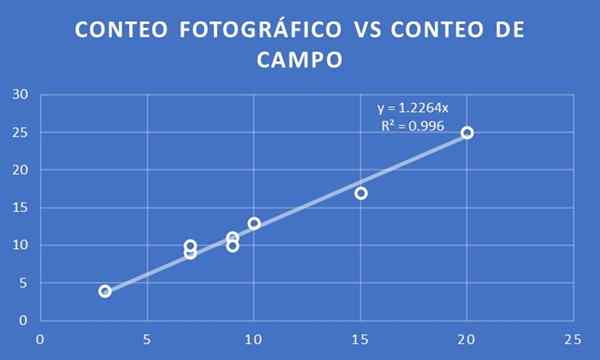Valokuvan lukumäärä verrattuna kenttämäärään. Lähde: f. Zapata.

Trendilinja säädetään ja sen kaltevuus määritetään. Tässä tapauksessa on saatu, että suhteellisuuskerroin on 1,23. Toisin sanoen, jos x on valokuvien lukumäärä, arvioidaan sitten, että kentän määrä on y = 1,23 x.

Sairasten lukumäärä 18 valitun erän valokuvan määrän mukaan: on:

18 x 8,5 = 153

Mutta koska koko metsä jaettiin 100 tonttiin samasta alueesta, valokuvausmenetelmällä arvioitu sairaiden puiden lukumäärä on: (100/18) x 153 = 850.

Pellon ja valokuvatutkimuksen vertailusta saatua korjauskerrointa sovelletaan nyt:

Arvioitu tosi sairaiden puiden lukumäärä metsässä = 1,23 x 850 = 1046.

Viitteet

1. Kaksinkertainen näyte suhteen arviointia varten, PennState College. PSU: sta haettu.Edu
2. Kaksinkertainen, moni- ja segeniaalinen näytteenotto, NC State University. Toipunut NCSU: sta.Edu
3. Yksinkertainen satunnainen näytteenotto. Toipunut Investopediasta.com
4. Mikä on kaksinkertainen näytteenotto? Toipunut: NIST.Hallitus
5. Näyte. Haettu: vuonna.Wikipedia.org
6. Monivaiheinen näyte. Haettu: vuonna.Wikipedia.org