Kertynyt taajuuskaava, laskenta, jakauma, esimerkit

Se kertynyt taajuus Se on absoluuttisten taajuuksien f, lapsesta, joka vastaa muuttujan tiettyä arvoa. Absoluuttinen taajuus on puolestaan ​​kuinka monta kertaa havainto näkyy tietojoukossa.

Tutkimusmuuttujan on selvää, että. Ja koska kertynyt taajuus saadaan lisäämällä absoluuttiset taajuudet, osoittautuu, että viimeisen tietojen kertynyt taajuus on vastattava niiden kokonaismäärän kanssa. Muuten laskelmissa on virhe.

Kertyneen taajuuden käytetään tilastotietojen hallinnassa

Yleensä kertynyt taajuus merkitään f: ksi_Yllyttää (Tai joskus n_Yllyttää), erottaa se absoluuttisesta taajuudesta F_Yllyttää Ja on tärkeää lisätä sarake siihen taulukkoon, jolla data on järjestetty, tunnetaan nimellä Taajuuspöytä.

Tällä tavoin helpotetaan muun muassa pitämään kertomus siitä, kuinka monta tietoa laskettiin tiettyyn havaintoon asti.

F_Yllyttää Se tunnetaan myös nimellä Absoluuttinen kertynyt taajuus. Jos jaat kokonaistietojen välillä, sinulla on Suhteellinen kertynyt taajuus, jonka lopullisen summan on oltava yhtä suuri kuin 1.

[TOC]

Kaavat

Muuttujan x tietyn arvon kertynyt taajuus_Yllyttää  Se on kaikkien arvojen absoluuttisten taajuuksien f, joka on pienempi tai yhtä suuri kuin:

F_Yllyttää  = f₁ + F₂ + F₃  +… F_Yllyttää

Lisäämällä kaikki absoluuttiset taajuudet, saadaan tiedon kokonaismäärä n, eli:

F₁ + F₂ + F₃ +.. . + F_n = N

Edellinen operaatio on kirjoitettu yhteenvetolla summan symbolilla ∑:

∑ f_Yllyttää = N

Muut kertyneet taajuudet

Seuraavat taajuudet voidaan myös kerätä:

-Suhteellinen taajuus: Se saadaan jakamalla absoluuttinen taajuus f_Yllyttää Kokonaistietojen välillä n:

F_{r -} = f_Yllyttää / N

Jos suhteelliset taajuudet lisätään lapsesta tiettyyn havaintoon vastaavaan, kertynyt suhteellinen taajuus. Viimeisen arvon on oltava yhtä suuri kuin 1.

-Kertynyt kertynyt taajuusprosentti: Kertynyt suhteellinen taajuus 100%: lla kerrotaan.

F_Prosentti = (f_Yllyttää / N) x 100%

Nämä taajuudet ovat hyödyllisiä tietojen käyttäytymisen kuvaamiseksi, esimerkiksi löytämällä keskeiset taipumusmittaukset.

Kuinka saada kertynyt taajuus?

Kertyneen taajuuden saamiseksi on tarpeen tilata tiedot ja järjestää ne taajuustaulukossa. Menettely on havainnollistettu seuraavassa käytännön tilanteessa:

Voi palvella sinua: yhdistetty peräkkäin

-Verkkokaupassa, joka myy matkapuhelimia, maaliskuun kuukauden tietyn tuotemerkin myyntitietue, seuraavat arvot päivässä:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Muuttuja on päivässä myytyjen puhelimien lukumäärä Ja se on kvantitatiivinen. Esitetyt tiedot eivät ole niin helppoja tulkita, esimerkiksi myymälän omistajat voisivat olla kiinnostuneita siitä, onko trendiä, kuten viikonpäiviä, jolloin kyseisen tuotemerkin myynti on suurempia.

Tämänkaltaiset tiedot ja muut, ne voidaan saada esittämällä tiedot järjestetyllä tavalla ja määrittelemällä taajuudet.

Kuinka täyttää taajuustaulukko

Kertyneen taajuuden laskemiseksi tiedot on tilattu:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Sitten on rakennettu taulukko, jossa on seuraavat tiedot:

-Ensimmäinen vasemmalla oleva sarake ja myytyjen puhelinten määrä, välillä 0–5 ja kasvavassa järjestyksessä.

-Toinen sarake: Absoluuttinen taajuus, joka on päivien lukumäärä, jotka myytiin 0 puhelinta, 1 puhelin, 2 puhelinta ja niin edelleen.

-Kolmas sarake: Kertynyt taajuus, joka koostuu edellisen taajuuden summasta sekä harkittavien tietojen taajuudesta.

Tämä sarake alkaa absoluuttisen taajuussarakkeen ensimmäisellä sarakkeella, tässä tapauksessa se on 0. Seuraavaa arvoa varten tämä lisätään edellisen kanssa. Siten kertyneen taajuuden viimeiset tiedot jatketaan, minkä on osuttava kokonaistietojen kanssa.

Taulukko

Seuraava taulukko näyttää muuttujan "Yhden päivän myytävien puhelimien lukumäärä", sen absoluuttinen taajuus ja sen kertyneen taajuuden yksityiskohtainen laskenta.

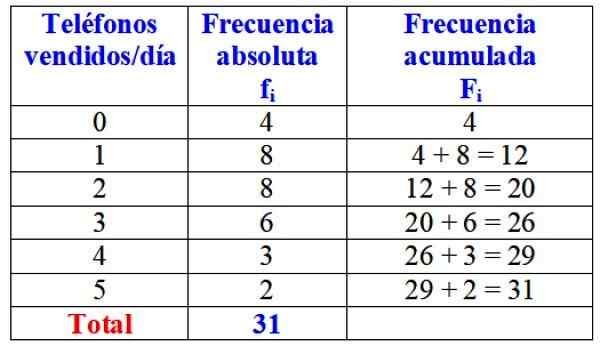Taulukko absoluuttisista ja kertyneistä taajuuksista muuttujalle "Myyty päivässä". Lähde: f. Zapata.

Ensi silmäyksellä voidaan sanoa, että kyseinen tuotemerkki myydään melkein aina yksi tai kaksi puhelinta päivässä, koska absoluuttisin taajuus on 8 päivää, mikä vastaa näitä muuttujan arvoja. Vain 4 päivän ajan kuukaudessa ei myynyt yhtä puhelinta.

Se voi palvella sinua: trigonometriset syyt: esimerkkejä, harjoituksia ja sovelluksia

Kuten todettiin, taulukon tutkiminen on helpompaa kuin alun perin kerätty löysä tieto.

Kertynyt taajuusjakauma

Kertyneen taajuuden jakauma on taulukko, jossa absoluuttiset taajuudet, kertyneet taajuudet, kertyneet suhteelliset taajuudet ja kertyneet prosentuaaliset taajuudet ovat saatavilla.

Vaikka eilen kaltaisen taulukon tietojen järjestämisen etuna havaitaan, jos tiedonumero on erittäin suuri, on mahdollista, että ne eivät riitä järjestämään niitä yllä, koska jos monet taajuudet ilmestyvät, se on silti vaikeaa tulkita.

Ongelma voi olla korjauskeino rakentamalla a Taajuusjakauma Väliajoin hyödyllinen menettely, kun muuttuja vie suuren määrän arvoja tai jos se on jatkuva muuttuja.

Tässä arvot on ryhmitelty samanlaisia ​​amplitudin väliajoihin, joita kutsutaan luokka. Luokille on ominaista: että sillä on:

-Luokkaraja: ovat kunkin aikavälin äärimmäiset arvot, niitä on kaksi, yläraja ja alaraja. Yleensä yläraja ei kuulu väliin, vaan välittömään seuraaviin, kun taas alaraja kuuluu.

-Luokan tuotemerkki: Se on kunkin aikavälin keskipiste, ja sitä pidetään sen edustavana arvona.

-Luokan leveys: Se lasketaan vähentämällä pää- ja pienimmän (alue) arvo ja jakamalla luokkien lukumäärä:

Luokan leveys = luokkien lukumäärä / lukumäärä

Sitten taajuusjakauman laatiminen on yksityiskohtainen.

Esimerkki

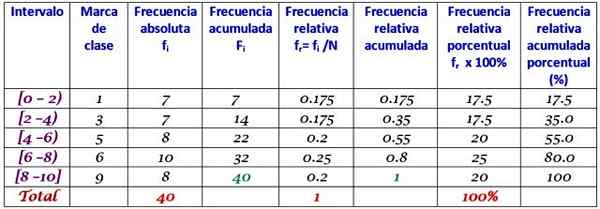
Tämä tietojoukko vastaa 40 matematiikkakokeen luokkaa asteikolla 0 - 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Taajuusjakauma tietyn määrän luokkien kanssa voidaan kehittää, esimerkiksi 5 luokkaa. On pidettävä mielessä, että monia luokkia käytettäessä tietoja ei ole helppo tulkita ja ryhmä kadonnut.

Voi palvella sinua: kuinka paljon sinun on lisättävä 3/4 saadaksesi 6/7?

Ja jos päinvastoin, ne on ryhmitelty hyvin harvoihin, niin tiedot laimennetaan ja osa niistä menetetään. Kaikki riippuu.

Tässä esimerkissä on hyvä idea saada kaksi pistettä kussakin välissä, koska pisteitä on 10 ja 5 luokkaa luodaan. Rank on vähennys pää- ja pienimmän luokituksen välillä, luokan leveys on:

Luokan leveys = (10-0)/5 = 2

Väliajat suljetaan vasemmalla ja avoinna oikealla (paitsi viimeinen), jota symboloidaan vastaavasti neliömäisillä kiinnikkeillä ja suluilla. Kaikilla on sama leveys, mutta se ei ole pakollinen, vaikkakin yleisin.

Jokainen aikaväli sisältää tietyn määrän elementtejä tai absoluuttista taajuutta, ja seuraavassa sarakkeessa on kertynyt taajuus, jossa summa kuljetetaan. Taulukko näyttää myös suhteellisen taajuuden f_{r -}  (Datan kokonaismäärän absoluuttinen taajuus) ja prosenttiosuusprosentti F_{r -} × 100%.

Ehdotettu harjoitus

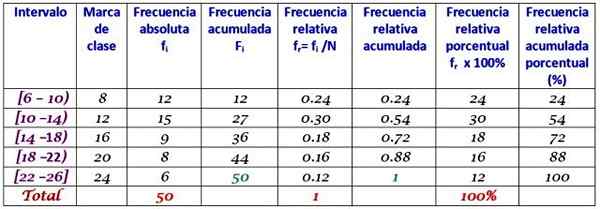
Yritys soitti päivittäisiä puheluita asiakkailleen vuoden kahden ensimmäisen kuukauden aikana. Tiedot ovat seuraavat:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

Ryhmä 5 luokkaa ja rakenna taulukko taajuuden jakautumisella.

Vastaus

Luokan leveys on:

(26-6)/5 = 4

Yritä ratkaista se ennen vastauksen näkemistä.

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
3. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
4. Todennäköisyys ja tilastot. Luokkavälin leveys. Haettu: Pedroprobabability and stadistist.Blogin.com.
5. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
6. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.