NULL -kulman määritelmä ja ominaisuudet, esimerkit, harjoitukset

Hän nollakulma Se on se, jonka mitta on 0 arvoa, sekä asteina että radianeissa tai muissa kulmien mittausjärjestelmässä. Siksi siitä puuttuu amplitudi tai avaaminen, kuten kahden rinnakkaisviivan välissä.

Vaikka sen määritelmä kuulostaa melko yksinkertaiselta, nollakulma on erittäin hyödyllinen monissa fysiikan ja tekniikan sovelluksissa, samoin kuin navigoinnissa ja suunnittelussa.

Kuvio 1. Auton nopeuden ja kiihtyvyyden välillä on nollakulma, joten auto menee nopeammin ja nopeammin. Lähde: Wikimedia Commons.

On fyysisiä määriä, jotka on kohdistettava rinnakkain tiettyjen vaikutusten saavuttamisen saavuttamiseksi: jos auto liikkuu suoraan moottoritiellä ja sen nopeusvektorin välillä v ja sen vektorikiinnitys -lla Siellä on 0º, auto kasvaa.

Seuraavassa kuvassa erityyppiset kulmat ilmestyvät, mukaan lukien nollakulma oikealle. Kuten voidaan nähdä, kulmasta 0 puuttuu amplitudi tai avaaminen.

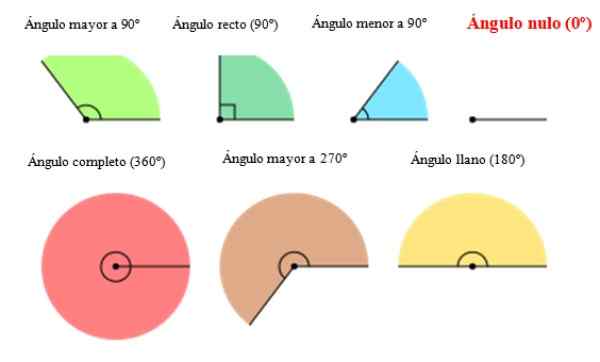Kuva 2. Kulmatyypit, mukaan lukien nollakulma. Lähde: Wikimedia Commons. Orias [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)].[TOC]

Esimerkkejä nollakulmista

On tiedossa, että yhdensuuntaiset viivat muodostavat kulman nolla. Kun sinulla on vaakasuora viiva, tämä on yhdensuuntainen Cartesian koordinaattijärjestelmän x -akselin kanssa, joten sen kallistus suhteessa siihen on 0. Toisin sanoen vaakasuuntaisilla viivoilla on nolla kaltevuus.

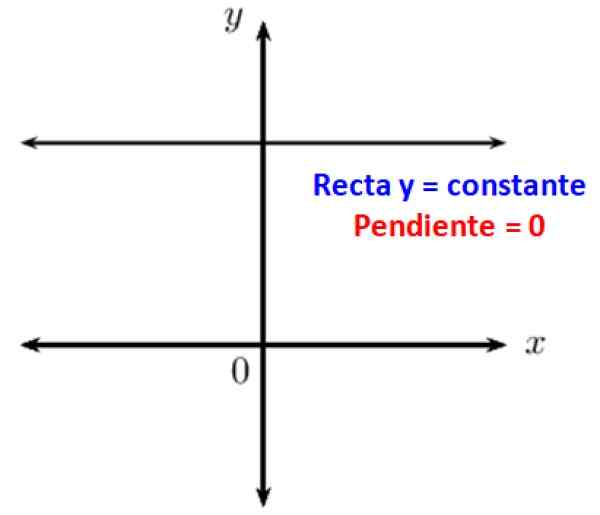Kuva 3. Vaakaviivoilla on nolla vireillä. Lähde: f. Zapata.

Myös nollakulman trigonometriset syyt ovat 0, 1 tai ääretön. Siksi nollakulmaa on läsnä monissa fyysisissä tilanteissa, joihin liittyy toimintoja vektoreilla. Nämä syyt ovat:

Voi palvella sinua: järjestetty pari

-SEN 0º = 0

-cos 0º = 1

-Tg 0º = 0

-s. 0º = 1

-Haittaa 0º → ∞

-Ctg 0º → ∞

Ja ne ovat hyödyllisiä analysoimaan joitain esimerkkejä tilanteista, joissa nollakulman esiintyminen on perustavanlaatuinen rooli:

- Nollakulman vaikutukset fyysisiin suuruuksiin

Vektorien summa

Kun kaksi vektoria on yhdensuuntainen, niiden välinen kulma on nolla, kuten yllä olevassa kuvassa 4 nähdään. Tässä tapauksessa molempien summa suoritetaan asettamalla yksi peräkkäin ja vektorisumman suuruus on lisäysten suuruussumma (kuva 4b).

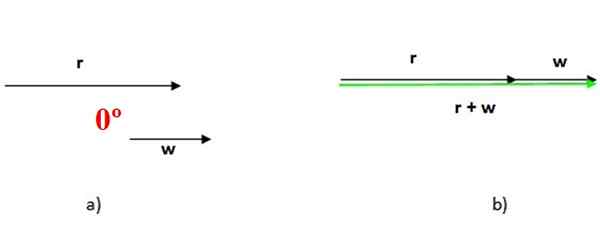Kuva 4. Rinnakkaisvektorien summa, tässä tapauksessa niiden välinen kulma on nollakulma. Lähde: f. Zapata.

Kun kaksi vektoria on yhdensuuntainen, niiden välinen kulma on nolla, kuten yllä olevassa kuvassa 4 nähdään. Tässä tapauksessa molempien summa suoritetaan asettamalla yksi peräkkäin ja vektorisumman suuruus on lisäysten suuruussumma (kuva 4b)

Vääntömomentti

Vääntömomentti tai vääntömomentti aiheuttaa rungon pyörimisen. Se riippuu kohdistetun voiman suuruudesta ja miten se sovelletaan. Erittäin edustava esimerkki on hahmon englanninkielinen avain.

Parhaan käännösvaikutuksen saavuttamiseksi voima kohtisuoraan koskee avainkahvaa joko ylös tai alas, mutta kiertoa ei odoteta, jos voima on yhdensuuntainen kahvan kanssa.

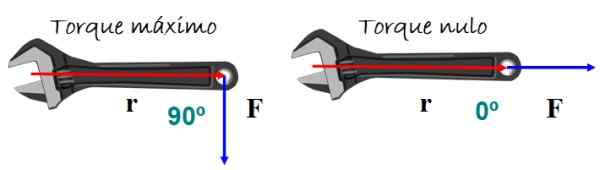Kuva 5. Kun sijainti- ja lujuusvektoreiden välinen kulma on tyhjyy. Lähde: f. Zapata.

Matemaattisesti vääntömomentti τ Se määritellään vektoriksi tai ristiintuotteeksi vektorien välillä r - (sijaintivektori) ja F Kuvion 5 (voimavektori):

Voi palvella sinua: Tilasto -oksat

τ = r x F

Vääntömomentin suuruus on:

τ = r f Sen θ

On θ kulma r - ja F. Kun sin θ = 0, vääntömomentti on tyhjä, siinä tapauksessa θ = 0º (tai myös 180º).

Sähkökenttävirta

Sähkökentän virtaus on skalaarinen suuruus, joka riippuu sähkökentän voimakkuudesta sekä pinnan suunnasta, jonka läpi se ylittää.

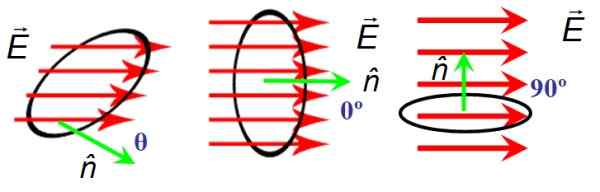
Kuviossa 6 on pyöreä pinta, jonka läpi sähkökenttäviivat kulkevat JA. Pinnan suunnan annetaan normaali vektori n. Vasemmalla puolella kenttä ja normaali vektori muodostavat mielivaltaisen kulman θ, keskustassa ne muodostavat nollakulman ja oikeat ovat kohtisuorassa.

Kun JA ja n Ne ovat kohtisuorassa, kenttäviivat eivät ylitä pintaa ja siksi virtaus on nolla, kun taas kulman välillä JA ja n Se on tyhjä, viivat ylittävät kokonaan pinnan.

Kreikan kirjaimella φ (lukee ”fi”), sen määritelmä yhtenäiselle kentälle kuten kuvassa, se pysyy näin:

Φ = JAOllan-Lla

Molempien vektorien keskellä oleva kohta tarkoittaa pistettä tai skalaarista tuotetta, joka vuorotellen määrittelee:

Φ = JAOllanA = eacosθ

Lihavoidut ja nuolet kirjeen yläpuolella ovat resursseja erottamaan vektori ja sen suuruus, joka on merkitty normaaleilla kirjaimilla. Koska cos 0 = 1, virtaus on maksimi, kun JA ja n Ne ovat yhdensuuntaisia.

Kuva 6. Sähkökentän virtaus riippuu pinnan ja sähkökentän välillä. Lähde: f. Zapata.

Harjoitukset

- Harjoitus 1

Kaksi voimaa P ja Q - Ne toimivat samanaikaisesti oikea -aikaisessa esineessä X, molemmat voimat muodostavat aluksi kulman θ niiden välillä. Mitä tapahtuu tuloksena olevan voiman suuruudelle, kun θ pienenee, kunnes se peruutetaan?

Voi palvella sinua: toimintojen arviointi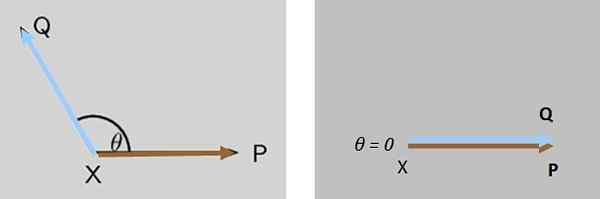 Kuva 7. Kahden kehoon vaikuttavan voiman välinen kulma vähenee, kunnes tuloksena olevan voiman suuruus saa tässä tapauksessa sen maksimiarvon. Lähde: f. Zapata.

Ratkaisu

Tuloksena olevan voiman suuruus Q - + P Se kasvaa vähitellen, kunnes se on maksimiarvo Q - ja P Ne ovat täysin yhdensuuntaisia ​​(kuva 7 oikea).

- Harjoitus 2

Ilmoita, onko nollakulma seuraavan trigonometrisen yhtälön ratkaisu:

cos 2x = 1 + 4se x

Ratkaisu

Trigonometrinen yhtälö on sellainen, jossa tuntematon on osa trigonometrisen syyn väitettä. Ehdotetun yhtälön ratkaisemiseksi on kätevää hyödyntää kaavaa kaksikulman kosiiniin:

cos 2x = cos² X - Sen² x

Koska tällä tavalla vasemmalla puolella olevasta väitteestä tulee x sijasta 2x. Niin:

koos² X - Sen² x = 1 + 4Sen x

Toisaalta cos² X + Sen² x = 1, niin:

koos² X - Sen² x = cos² X + Sen² x + 4Sen x

Termi cos² X peruutetaan ja pysyy:

- Senttiä² x = Sen² x + 4sen x → - 2sen² x - 4Senx = 0 → 2Sen² x + 4Senx = 0

Nyt seuraava muuttujan muutos tehdään: senx = u ja yhtälö muutetaan:

2U² + 4U = 0

2U (U+4) = 0

Kenen ratkaisut ovat: u = 0 ja u = -4. Palauttamalla muutoksen meillä olisi kaksi mahdollisuutta: sin x = 0 ja senx = -4. Tämä viimeinen ratkaisu ei ole elinkelpoinen, koska minkä tahansa kulman rinta on välillä -1 ja 1, joten meillä on ensimmäinen vaihtoehto:

sin x = 0

Siksi x = 0º on ratkaisu, mutta palvelee myös mitä tahansa kulmaa, jonka sini on 0, joka voi olla myös 180º (π radianit), 360º (2 π radians) ja myös vastaavat negatiivit.

Trigonometrisen yhtälön yleisin ratkaisu on: x = kπ missä k = 0, ± 1, ± 2, ± 3, .. . k kokonaisluku.

Viitteet

1. Baldor, a. 2004. Litteä ja avaruusgeometria trigonometrialla. Kulttuurjulkaisut S.-Lla. C: n.V. Meksiko.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 3. Hiukkasjärjestelmät. Toimittanut Douglas Figueroa (USB).
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköinen vuorovaikutus. Toimittanut Douglas Figueroa (USB).
4. Onlinemathearning. Kulmatyypit. Haettu: OnlinemathLearning.com.
5. Zill, D. 2012. Algebra, trigonometria ja analyyttinen geometria. McGraw Hill Inter -American.