Sisäiset ja ulkoiset konjugoituja kulmia esimerkkejä, harjoituksia

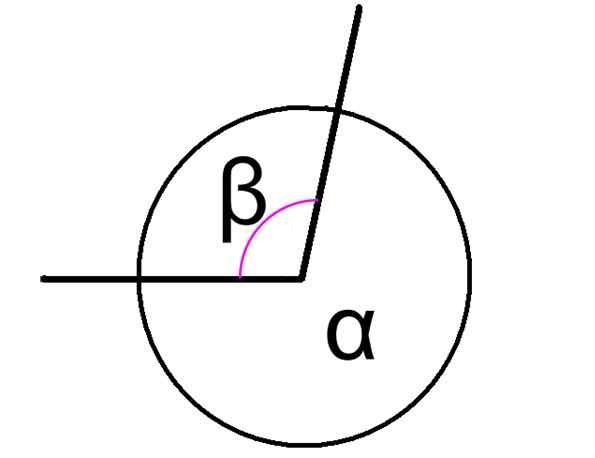
Se konjugoitu kulma Ne lisätään 360 °: n seurauksena riippumatta siitä, ovatko nämä kulmat vierekkäin vai eivät. Kuvio 1 esittää kaksi konjugoitua kulmaa, jotka on merkitty a ja β: ksi.

Tällöin kuvion kulmilla α ja β on yleinen kärki ja niiden sivut ovat yleisiä, joten ne ovat vierekkäisiä. Niiden välinen suhde ilmaistaan ​​seuraavasti:

α + β = 360º

Kuvio 1. Kaksi konjugoitua keskikulmaa, summa. Lähde: Wikimedia Commons. Ei konetta luettavissa olevaa kirjailijaa. Thiago R Ramos oletettu (perustuen tekijänoikeusvaatimuksiin). [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/)] Se on kulmien luokittelu sen summan mukaan. Muita tärkeitä määritelmiä ovat täydentävät kulmat, jonka summa on 90 º ja lisäkulmat, joka on yhteensä 180 º.

Toisaalta tarkastellaan nyt kahta rinnakkaista viivaa, jotka ovat leikkaamassa, joiden asennus on sitten esitetty:

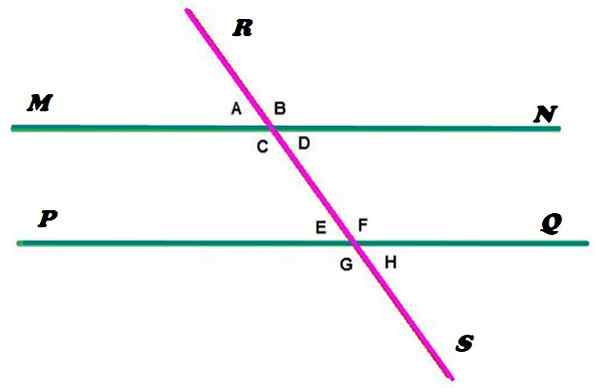
Kuva 2. Rinnakkaiset viivat leikkaa secant. Lähde: f. Zapata.

MN- ja PQ -viivat ovat yhdensuuntaisia, kun taas RS -viiva kuivuu, leikkaa rinnakkaisuuksia kahdessa pisteessä. Kuten voidaan nähdä, tämä kokoonpano määrittää 8 kulman muodostumisen, johon se on merkitty pienillä kirjaimilla.

No, alussa annetun määritelmän mukaan kulmat A, B, C ja D on konjugoitu. Ja samalla tavalla ne ovat E, F, G ja H, koska molemmat tapaukset toteutetaan:

A+B+C+D = 360º

JA

E+F+G+H = 360º

Tätä kokoonpanoa varten kaksi kulmaa konjugoitiin, jos ne ovat samalla puolella RS -kuivauslinjan suhteen ja molemmat ovat sisäisiä tai ulkoisia. Ensimmäisessä tapauksessa on puhetta kulmista Sisäiset konjugaatit, Toisessa ollessaan ne ovat kulmia ulkoinen konjugaatti.

[TOC]

Esimerkit

Kuviossa 2 ulkoiset kulmat ovat niitä, jotka ovat MN- ja PQ -linjojen rajaamat alueen ulkopuolella, kulmat A, B, G ja H. Kun taas kahden viivan välissä olevat kulmat ovat C, D, E ja F.

Voi palvella sinua: Coplanares -pisteet: Yhtälö, esimerkki ja ratkaisut harjoitukset

Nyt on tarpeen analysoida, mitkä kulmat ovat vasemmalla ja mitkä Secantin oikealla puolella.

R: n vasemmalla puolella ovat kulmat A, C, E ja G. Ja oikealla ovat B, D, F ja H.

Jatkamme välittömästi konjugoitujen kulmien parien määrittämistä edellisen osan määritelmän mukaan:

-A ja g, ulkoinen ja vasemmalla puolella Rs.

-D ja F, sisäinen ja Rs: n oikealla puolella.

-B ja H, ulkoinen ja oikealla puolella Rs.

-C ja E, sisäinen ja vasemmalla puolella Rs.

Konjugoitujen kulmien ominaisuus rinnakkaisten viivojen välillä

Rinnakkaisten viivojen väliset konjugoivat kulmat ovat lisäyksiä, ts. Niiden summa on yhtä suuri kuin 180 °. Tällä tavoin kuviolle 2 seuraava on toteutettu:

A + G = 180º

D + F = 180º

B + H = 180º

C + E = 180º

Vastaavat kulmaparit yhdensuuntaisille viivoille

He ovat niitä, jotka ovat kuivumislinjan samalla puolella, ne eivät ole vierekkäisiä ja yksi niistä on sisäinen ja toinen ulkoinen. On tärkeää visualisoida ne, koska niiden mitta on sama, koska ne ovat vastakkaisia ​​kulmia kärjen vieressä.

Palattuaan kuvaan 2 vastaavat kulmat tunnistetaan seuraavasti:

-A ja E

-C ja g

-B ja f

-D ja h

Neljänneksen sisäkulmat

Neljännekset ovat 4 -puolta monikulmioita, mukaan lukien neliö, suorakulmio, trapetsi, rinnakkaisgrammi ja esimerkiksi rhombus, esimerkiksi. Riippumatta muodosta, missä tahansa heistä on täytetty, että sen sisäkulmien summa on 360º, siksi ne noudattavat alussa annettua määritelmää.

Tarkastellaan joitain esimerkkejä neljänneksistä ja kuinka laskea sen sisäiset kulmat edellisten osien tietojen mukaan:

Voi palvella sinua: mitkä ovat kehän 7 elementtiä?

Esimerkit

a) Kolme nelinkertaisen mittauksen kulmasta 75º, 110º ja 70º. Kuinka paljon jäljellä olevan kulman mittauksen tulisi?

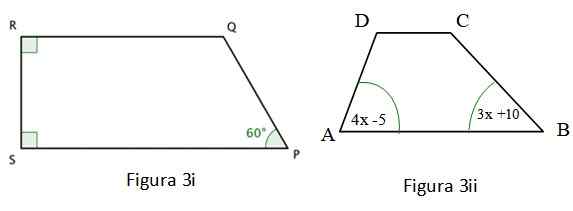
b) Löydä kulman ∠Q -arvo kuvassa 3 I.

c) Laske, kuinka paljon mittaa kuvan 3 II kulma ∠A.

Liittää jhk

Olkoon α puuttuva kulma, se täyttyy:

α + 75 º + 110º + 70º = 360 → α = 105º

Ratkaisu b

Kuvio 3i on esitetty a Trapetsoidi Ja kaksi sen sisäkulmasta ovat suorat, jotka on korostettu värien neliöllä kulmissa. Tätä kvadrilateriaalia varten seuraava on varmennettu:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90º; ∠P = 60º

Siksi:

∠ Q = 2 x 90º + 60º = 240º

Liuos C

Kuvio 3 II: n nelikulmainen on myös trapetsi, jolle seuraava täytetään:

∠A + ∠B + ∠C + ∠D = 360º

Siksi:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Lauseessa pyydetyn kulman määrittämiseksi käytetään, että ∠A = 4x - 5. Aikaisemmin lasketun x -arvon korvaaminen on noudatettu, että ∠A = (4 × 25) -5 = 95º

Harjoitukset

- Harjoitus 1

Tietäen, että yksi esitetyistä kulmista on 125 arvoinen, jäljellä olevien seitsemän kulman mittaukset seuraavassa kuvassa ja vastausten perusteleminen.

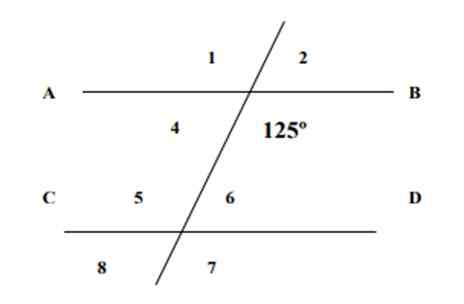Kuva 4. Harjoituksen 1 viivat ja kulmat. Lähde: f. Zapata.

Ratkaisu

Kulma 6 ja kulma 125 ovat sisäisiä konjugaatteja, joiden summa on 180º: n arvoinen konjugoitujen kulmien ominaisuuden mukaan: siksi:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

Toisaalta ∠6 ja ∠8 ovat vastakkaisia ​​kulmia kärkipisteellä, jonka mitta on sama. Siksi ∠8: n mitat ovat 55º.

Voi palvella sinua: Vector Algebra

Kulmaa ∠1 vastustaa myös kärkipisteessä 125, niin voimme vahvistaa, että ∠1 = 125º. Voimme myös vedota siihen tosiasiaan, että vastaavilla kulmapareilla on sama toimenpide. Kuvassa nämä kulmat ovat:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Harjoitus 2

Löydä x: n arvo seuraavasta kuvasta ja kaikkien kulmien arvot:

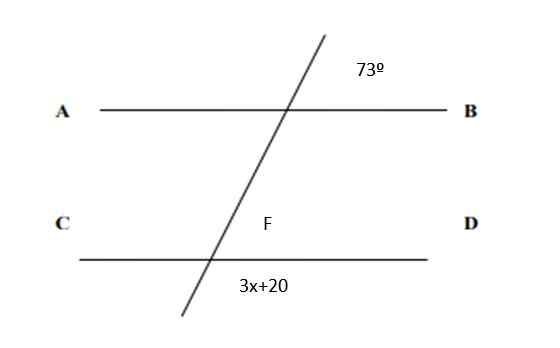Kuva 5. Linjat ja kulmat harjoitukselle 2. Lähde: f. Zapata.

Ratkaisu

Koska ne ovat vastaavia pareja, seuraa, että f = 73º. Ja toisaalta konjugoitujen parien summa on 180º, siksi:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Lopuksi x: n arvo on:

x = 87/3 = 29

Kaikkien kulmien osalta ne ilmestyvät seuraavassa kuvassa:

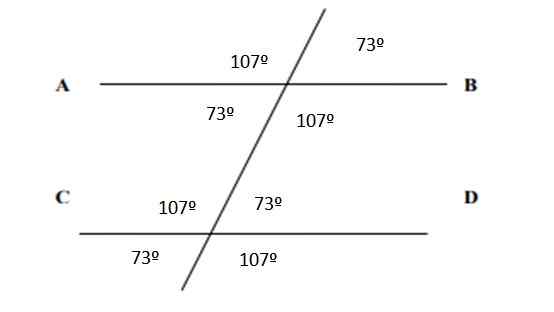Kuva 6. Kulmat, jotka johtavat harjoitukseen 2. Lähde: f. Zapata.

Viitteet

1. Kulmaryhmät. Täydentävä, lisä- ja selityskulma selitys. Toipunut: TÄMÄGET.com/
2. Baldor, a. 1983. Litteä ja tila ja trigonometriageometria. Kulttuuriryhmä.
3. Corral, M. Matematiikka LibretTexts: Kulmat. Toipunut: matematiikka.Librettexts.org.
4. Mathmania. Luokittelemalla ja rakentamalla kulmia mittauksella. Toipunut: Mathemania.com/
5. Wentworth, G. Planeetan geometria. Toipunut: Gutenberg.org.
6. Wikipedia. Konjugoitu kulma. Palautettu: on.Wikipedia.org.