Coplanares -pisteyhtälö, esimerkki ja ratkaistu harjoitus

Se Coplanares -pisteet Ne kaikki kuuluvat samaan lentokoneeseen. Kaksi pistettä ovat aina koplanareja, koska nämä kohdat määrittelevät linjan, jonka läpi tasaiset äärettömät kulkevat. Sitten molemmat kohdat kuuluvat jokaiseen linjan läpi kulkeviin suunnitelmiin ja siksi ne ovat aina koplaaneja.

Toisaalta kolme pistettä määrittelevät yhden tason, jonka seurataan, että kolme pistettä on aina koplanares määrittämäänsä tasoon.

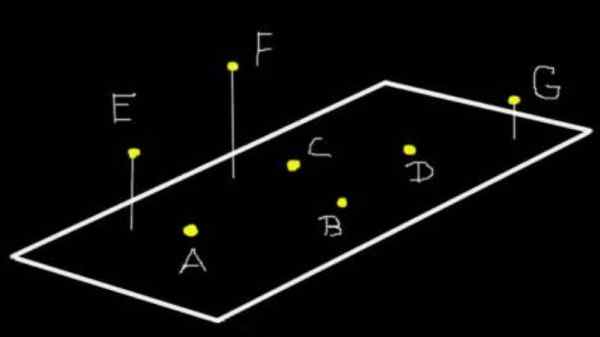
Kuvio 1. A, B, C ja D Ne ovat koplaaneja tasoon (ω). E, F ja G eivät ole koplanareja A (ω), mutta jos ne ovat koplaaneja tasolle, joka kolme määrittelee. Lähde: f. Zapata.

Yli kolme pistettä voi olla koplanaaria tai ei. Esimerkiksi kuviossa 1 pisteet A, B, C ja D ovat koplaaneja tasoon (ω). Mutta e, f ja g eivät ole koplanareja A (ω), vaikka ne ovatkin koplaanit tasolle, jotka kolme määrittelevät.

[TOC]

Tason yhtälö annettiin kolme pistettä

Kolmella tunnetulla pisteellä A, B, C määritetyn tason yhtälö on matemaattinen suhde, joka takaa, että mikä tahansa geneeristen koordinaattien (x, y, z) piste P, joka täyttää yhtälön, kuuluu mainitulle tasolle. 

Aikaisempi lausunto vastaa sitä, että sanominen, että jos koordinaatin (x, y, z) kohtaavat Plan -yhtälön, niin mainittu kohta on Copatarin kolmen pisteen A, B, C kanssa, joka määritteli tason.

Aloitetaan etsimällä vektorit etsimällä mainitun tason yhtälön Ab ja Ac-

Ab = [Bx - kirves, by - ay, bz - az]

Ac = [Cx - kirves, cy - ay, cz - az]

Vektorituote Ab X Ac Se johtaa kohtisuoraan tai normaaliin vektoriin tasolle, joka määritetään pisteillä A, B, C.

Mikä tahansa koordinaattien (x, y, z) kohta kuuluu tasoon, jos on totta, että vektori AP on kohtisuorassa vektoriin nähden Ab X Ac, joka on taattu, jos se on toteutettu:

Voi palvella sinua: Decagon: säännöllinen, epäsäännöllinen, ominaisuudet, esimerkit

AP • (AB X Ac) = 0

Tämä vastaa sanomista, että kolminkertainen tuote AP, Ab ja Ac Olla nolla. Aikaisempi yhtälö voidaan kirjoittaa matriisilla:

Esimerkki

Olkoon pisteet A (0, 1, 2); B (1, 2, 3); C (7, 2, 1) ja D (-lla, 0, 1). Minkä arvon pitäisi olla -lla niin, että neljä pistettä ovat koplanares?

Ratkaisu

A: n arvon löytämiseksi on välttämätöntä, että piste D on osa tasoa määritettynä A, B ja C, mikä taataan, jos tasoyhtälö kohtaa.

Kehitetään determinantti, joka meillä on:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

Aikaisempi yhtälö osoittaa sen A = -1 Tasa -arvon toteuttaminen. Toisin sanoen ainoa tapa, jolla se kohta D (-lla, 0,1) olla koplanaari pisteillä A, B ja C on se -lla Valga -1. Muuten se ei ole koplanar.

Ratkaisut

- Harjoitus 1

Taso leikkaa Cartesian akselit x, y, z 1, 2 ja 3. Mainitun tason leikkaus akselien kanssa määrittää pisteet A, B ja C. Löydä pisteen D DZ -komponentti, jonka kartesian komponentit ovat:

 D (-DZ, DZ+1, DZ) 

Ehdolla, että d on koplanaari pisteillä A, B ja C. 

Ratkaisu

Kun Cartesian -akselien kanssa on tason sieppauksia, voidaan käyttää tasoyhtälön segmenttistä muotoa:

x/1 + y/2 + z/3 = 1

Kuten kohta D on kuultava edelliseen tasoon, sinun on:

-Dz/1 + (dz + 1)/2 + dz/3 = 1

Tarkoittaen:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

DZ (-1/6⅙) = ½ 

DZ = -3 

Yllä olevasta se seuraa sitä pistettä D (3, -2, -3) on kytketty pisteillä A (1, 0, 0); B (0, 2, 0) ja C (0, 0, 3).

Se voi palvella sinua: kolmiomaiset samankaltaisuuskriteerit

- Harjoitus 2

Määritä, onko pisteitä A (0, 5, 3); B (0, 6, 4); C (2, 4, 2) ja D (2, 3, 1) ovat koplaaneja.

Ratkaisu

Muodostamme matriisin, jonka rivat ovat D-A: n, B-A: n ja C-A: n koordinaatit. Silloin determinantti lasketaan ja varmistetaan, onko nolla.

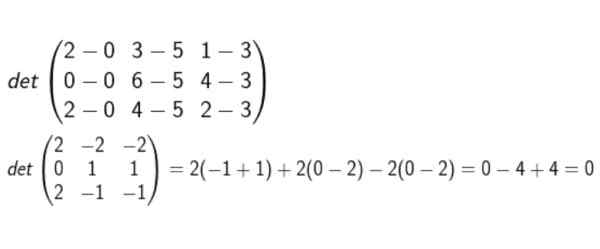
Kaikkien laskelmien suorittamisen jälkeen päätellään, että ne ovat koplaaneja.

- Harjoitus 3

Kaksi riviä annetaan avaruudessa. Yksi niistä on viiva (R), jonka parametrinen yhtälö on:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

Ja toinen on viiva (t), joiden yhtälö on:

(S): x + 2 y = 1; Z = -1

Osoita, että (r) ja (s) ne ovat suorat koplanarium, ts. He ovat samassa tasossa.

Ratkaisu

Aloitetaan mielivaltaisesti kaksi pistettä linjalla (R) ja kaksi linjalla (t):

Suora (r): λ = 0; A (1, 1, 1) ja λ = 1; B (3, 0, 1)

Tehdään x = 0 linjalla=> y = ½; C (0, ½, -1). Ja toisaalta, jos teemme y = 0 => x = 1; D (1, 0, -1).

Eli olemme ottaneet pisteitä A ja B, jotka kuuluvat linjaan (r) ja pisteisiin C ja D pisteisiin, jotka kuuluvat linjaan (t). Jos nämä kohdat ovat koplaaneja, niin myös nämä kaksi linjaa ovat.

Nyt päätämme osoittaa kuinka kääntö ja sitten löydämme vektorien koordinaatit Ab, Ac ja ILMOITUS. Tällä tavalla saat:

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => ILMOITUS= (0, -1, -2)

Seuraava vaihe on rakentaa ja laskea determinantti, jonka ensimmäinen rivi on vektorikertoimet Ab, Toinen rivi on Ac ja kolmas rivi vektorin ILMOITUS-

Voi palvella sinua: Miletus sellainen lause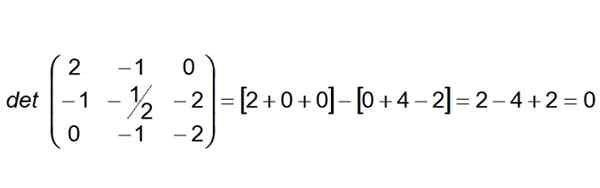

Kuten determinantti osoittautuu nollaksi, niin voimme päätellä, että neljä pistettä ovat koplanarioita. Lisäksi voidaan sanoa, että linjat (R) ja (S) ovat myös koplaaneja.

- Harjoitus 4

Linjat (R) ja (S) ovat koplaaneja, kuten harjoituksessa 3 osoitetaan. Löydä niitä sisältävän tason yhtälö.

Ratkaisu

Pisteet A, B, C määrittelevät kokonaan kyseisen tason, mutta haluamme määrätä, että mikä tahansa koordinaattien piste X (x, y, z) kuuluvat samaan.

X - a: (x -1, y -1, z - 1) => Kirves= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -a: (0-1, 1/2 -1, -1 -1) => Ac= (-1, -1/2, -2)

Niin että x kuuluu A: n, B: n, C: n määrittelemään tasoon ja jossa linjat (R) ja (S) ovat, on välttämätöntä, että sen ensimmäiseen riviin muodostettu determinantti kumoaa komponentit Kirves, toisessa Ab Ja kolmannessa Ac-

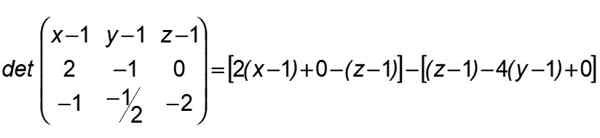
Tämän tuloksen jälkeen ryhmittelemme tällä tavalla:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

Ja heti nähdään, että se voidaan kirjoittaa uudelleen näin:

x - 1 + 2y - 2 - z + 1 = 0

Siksi x + 2y - z = 2 on tason yhtälö, joka sisältää viivat (r) ja (s).

Viitteet

1. Fleming, w. 1989. Prealculus -matematiikka. Prentice Hall Ptr.
2. Kolman, b. 2006. Lineaarialgebra. Pearson -koulutus.
3. Uskollinen, j. M. 2005. Litteä analyyttinen geometria. Mérida - Venezuela: Venezuelan toimituksellinen C. -Lla.
4. Navarro, Rocio. Vektorit. Toipunut: Kirjat.Google.yhteistyö.mennä.
5. Pérez, c. D -d. 2006. Ennakkoluulo. Pearson -koulutus.
6. Prenowitz, w. 2012. Geometrian peruskäsitteet. Rowman & Littlefield.
7. Sullivan, M. 1997. Ennakkoluulo. Pearson -koulutus.