Lisäkulmat, jotka ovat laskelmia, esimerkkejä, harjoituksia

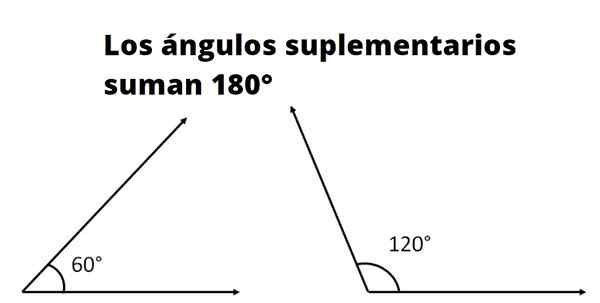
Kaksi tai useampaa on lisäkulmat Jos sen mittojen summa vastaa tasaisen kulman mittausta. Litteän kulman mitta, jota kutsutaan myös tasaiseksi kulmaksi, asteina on 180º ja radianeissa π.

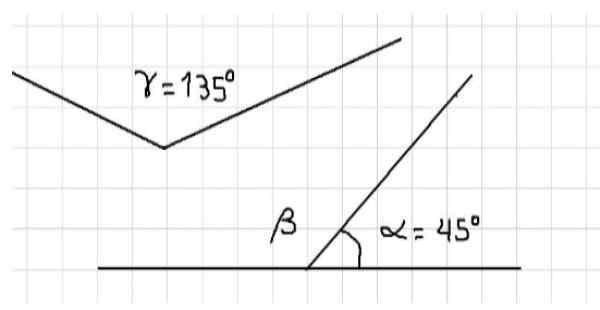
Esimerkiksi havaitsemme, että kolmion kolme sisäkulmaa ovat täydentäviä, koska sen mittojen summa on 180º. Kolme kulmaa on esitetty kuvassa 1. Edellä mainitusta seuraa, että α ja β ovat täydentäviä, koska ne ovat vierekkäisiä ja niiden koko summa tasainen kulma.

Kuvio 1: α ja β ovat täydentäviä. α ja γ ovat täydentäviä. Lähde: f. Zapata.

Myös samassa kuvassa on kulmia α ja γ, jotka ovat myös täydentäviä, koska niiden mittojen summa on yhtä suuri kuin tasaisen kulman laajuus, ts. 180º. Ei voida sanoa, että kulmat β ja y ovat täydentäviä, koska ne ovat molemmat putouskulmat, niiden mitat ovat suurempia kuin 90º ja siksi sen summa ylittää 180º.

Lähde: Lafer.com

Toisaalta voidaan sanoa, että kulman p -mitta on yhtä suuri kuin kulman γ mita, koska jos β on a ja γ lisäys, on a -lisäys, niin β = γ = 135º.

[TOC]

Esimerkit

Seuraavissa esimerkeissä pyydetään löytämään tuntemattomat kulmat, jotka on merkitty kuulustelulla kuvassa 2. Ne vaihtelevat yksinkertaisimmista esimerkeistä hieman yksityiskohtaisemmin kuin lukijan tulisi olla varovaisempi.

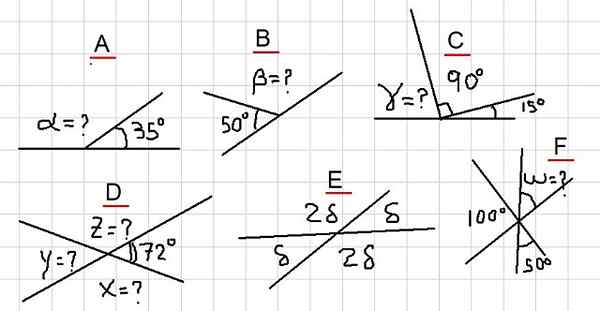Kuva 2. Erilaisia ​​esimerkkejä lisäkulmista. Lähde: f. Zapata.

Esimerkki a

Kuvassa meillä on, että viereiset kulmat α ja 35º lisäävät tasaisen kulman. Ts. Α + 35º = 180º ja siksi on toteutettu, että: α = 180º- 35º = 145º.

Esimerkki b

Koska β on täydentävä 50º: n kulmassa, seurataan, että β = 180º - 50º = 130º.

Voi palvella sinua: mitkä ovat vertauksen elementit? (Osat)

Esimerkki C

Kuviosta 2C havaitaan seuraava summa: γ + 90º + 15º = 180º. Ts. Γ on täydentävä kulmalla 105º = 90º + 15º. Silloin päättyy: 

γ = 180º- 105º = 75º

Esimerkki D

Koska x on täydentävä 72º: lla, seuraa, että x = 180º - 72º = 108º. Lisäksi ja se on täydentävä x, sitten Y = 180º - 108º = 72º.

Ja lopuksi z on täydentävä 72º: lla, joten z = 180º - 72º = 108º.

Esimerkki E

Kulmat δ ja 2δ ovat lisäaikaisia, siksi Δ + 2δ = 180º. Mikä tarkoittaa, että 3A = 180º, ja tämä puolestaan ​​sallii kirjoittamisen: Δ = 180º / 3 = 60º.

Esimerkki f

Jos kutsumme 100º: n ja 50º: n välistä kulmaa, se on tarpeen täydentää heille, koska havaitaan, että niiden koko summa tasainen kulma.

Tästä seuraa, että u = 150º. Kuten u vastustaa kärkipistettä W: lle, sitten w = u = 150º.

Harjoitukset

Seuraavassa ehdotetaan kolme harjoitusta, kaikissa niissä kulmien A ja B arvo on löydettävä asteina, joten kuviossa 3 esitetyt suhteet täyttyvät. Lisäkulmien käsitettä käytetään kaikkien ratkaisussa.

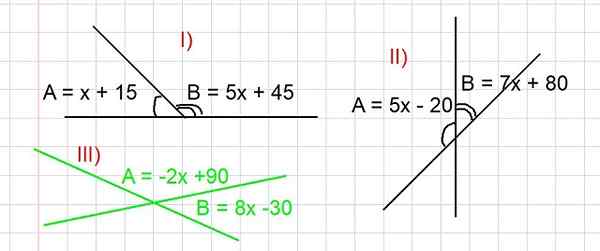Kuva 3. Kuva ratkaista harjoitukset I, II ja III lisäkulmista. Kaikki kulmat ilmaistaan ​​asteina. Lähde: f. Zapata.

- Harjoitus I

Määritä kuvan 3 osan A ja B arvot).

Ratkaisu

A ja B ovat täydentäviä, missä A + B = 180 astetta on vaihdettava, sitten A: n ja B: n lauseke korvataan X: n funktiona, kuten kuvassa näkyy:

(x + 15) + (5x + 45) = 180

Ensimmäisen tilauksen lineaarinen yhtälö saadaan. Sen ratkaisemiseksi termit heitetään pois: termit:

6 x + 60 = 180

Voi palvella sinua: Real numerot: historia, esimerkit, ominaisuudet, toiminnot

Molempien jäsenten jakaminen 6: n välillä ovat:

x + 10 = 30

Ja lopuksi puhdistaminen seuraa, että x on 20º: n arvoinen.

Nyt X: n arvo on vaihdettava tilatut kulmat löytämiseksi. Sieltä sinun on kulma A on: A = 20 +15 = 35º.

Ja sen puolestaan ​​kulma B on B = 5*20 + 45 = 145º.

- Harjoitus II

Löydä kuvan 3 osan A ja B arvot.

Ratkaisu

A ja B ovat lisäkulmia, A + B = 180 astetta on. A: n ja B: n ekspression korvaaminen osassa II) 3 funktiona on:

(-2x + 90) + (8x - 30) = 180

Uudelleen saadaan ensimmäisen asteen yhtälö, jolle termit on oltava kätevästi ryhmä:

6 x + 60 = 180

Molempien jäsenten jakaminen 6: n välillä ovat:

x + 10 = 30

Missä seuraa, että x on 20º: n arvoinen.

Toisin sanoen kulma a = -2*20 + 90 = 50 °. Kun taas kulma B = 8*20-30 = 130.

- Harjoitus III

Määritä kuvion 3 osan A ja B arvot) (vihreänä).

Ratkaisu

A ja B ovat lisäkulmia, A + B = 180 astetta on. A: n ja B: n lauseke on vaihdettava kuvassa 3 esitetyn x: n funktiona, joka sinulla on:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Jakamalla molemmat jäsenet 12: lla X: n arvon tyhjentämiseksi, sinulla on:

x + 5 = 15

Lopuksi todetaan, että X on 10 astetta arvoinen.

Jatka vaihtamista löytääksesi kulman A: A = 5*10 -20 = 30 °. Ja kulmalle B: B = 7*10 + 80 = 150º

Voi palvella sinua: mikä on tilastoalue? (Esimerkkejä)

Lisäkulmat kahdessa rinnakkaisessa leikkauksessa

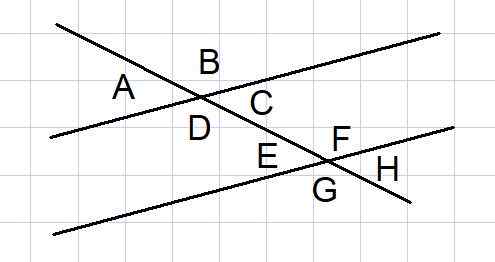Kuva 4. Kahden rinnakkaisen väliset kulmat leikkaavat. Lähde: f. Zapata.

Kaksi Secantin leikkaamista rinnakkaisviivaa on tavallinen geometrinen rakenne joissakin ongelmissa. Tällaisten viivojen joukossa muodostuu 8 kulmaa, kuten kuvassa 4 esitetään.

Näistä 8 kulmasta jotkut kulmaparit ovat lisäainetta, jotka luetellaan alla:

1. Ulkoiset kulmat ja B ja ulkopuoliset G ja H
2. Sisustuskulmat D ja C ja sisätilat E ja F
3. Ulkoiset kulmat a ja g sekä ulkoiset b ja h
4. Sisäiset kulmat d ja e ja vangit C ja F

Täydellisyyden mukaan myös yhtäläiset kulmat on nimetty:

1. Sisäiset vuorottelut: D = F ja C = E
2. Ulkoiset vuorottelut: a = h ja b = g
3. Vastaavat: a = e ja c = h
4. Vertex A = C ja E = H: n vastakohdat
5. Vastaavat: b = f ja d = g
6. Vertex B = D ja F = G vastakkaiset vastakohdat

- Harjoitus IV

Viittauksessa kuvioon 4, jossa kulmat osoittavat kahden rinnakkaisen viivan välillä, jotka on leikattu sekaantilla, kaikkien radiaanien kulmien arvo tietäen, että kulma A = π/6 radiaanit.

Ratkaisu

A ja B ovat lisäkulmia, joten b = π - a = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Viitteet

1. Baldor, J. -Lla. 1973.Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-. 
2. Matemaattiset lait ja kaavat. Kulman mittausjärjestelmät. Haettu: Ingemecanica.com.
3. Wentworth, G. Planeetan geometria. Toipunut: Gutenberg.org.
4. Wikipedia. Lisäkulmat. Palautettu: on.Wikipedia.com
5. Wikipedia. Kuljettaja. Palautettu: on.Wikipedia.com
6. Zapata f. Goniometri: Historia, osat, toiminta. Haettu: Lifer.com