Kompleksilukujen ominaisuudet, esimerkit, toiminnot

Se kompleksilukut Ne ovat numeerinen sarja, joka kattaa polynomien todelliset numerot ja kaikki juuret, mukaan lukien negatiivisten lukujen tasaiset juuret. Näitä juuria ei ole reaalilukujen sarjassa, mutta monimutkaisina lukuina on ratkaisu.

Monimutkainen numero koostuu todellisesta osasta ja toisesta nimeltään "kuvitteellinen". Todellista osaa kutsutaan -lla, Esimerkiksi ja kuvitteellinen osa Ib, kanssa -lla ja b - Todelliset numerot ja "pidän" Kuvitteellinen yksikkö. Tällä tavoin kompleksinumero on lomake:

Z = A + IB

Kuvio 1.- Kompleksilukujen binomiaalinen esitys todellisen osan ja kuvitteellisen osan suhteen. Lähde: Pixabay.

Esimerkkejä kompleksilukuista ovat 2 - 3i, -πi, 1 + (1/2) i. Mutta ennen heidän kanssaan toimintaa, katsotaanpa mistä kuvitteellinen yksikkö on peräisin Yllyttää, Tämän neliömäisen yhtälön huomioon ottaminen:

x² - 10x + 34 = 0

Jossa a = 1, b = -10 ja c = 34.

Kun liuotinkaavaa käytetään ratkaisun määrittämiseen, löydämme seuraavat:

Kuinka määrittää √-36: n arvo? Ei ole todellista numeroa, että neliö on negatiivinen määrä. Sitten päätellään, että tällä yhtälöllä ei ole todellisia ratkaisuja.

Voimme kuitenkin kirjoittaa tämän:

√-36 = √-6² = √6² (-1) = 6√-1

Jos määrittelemme tietyn arvon x sellainen:

x² = -1

Niin:

x = ± √-1

Ja aikaisemmassa yhtälössä olisi ratkaisu. Siksi kuvitteellinen yksikkö määritettiin seuraavasti:

I = √-1

Ja niin:

√-36 = 6i

Monet antiikin matemaatikot työskentelivät samanlaisten ongelmien ratkaisemiseksi korostaen renessanssin Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) ja Raffaele Bombelli (1526-1572).

Vuosia myöhemmin René Descartes (1596-1650) kutsutaan "kuvitteelliseksi" määriin, kuten esimerkin √-36. Tästä syystä √-1 tunnetaan nimellä Kuvitteellinen yksikkö.

[TOC]

Kompleksinumerot ominaisuudet

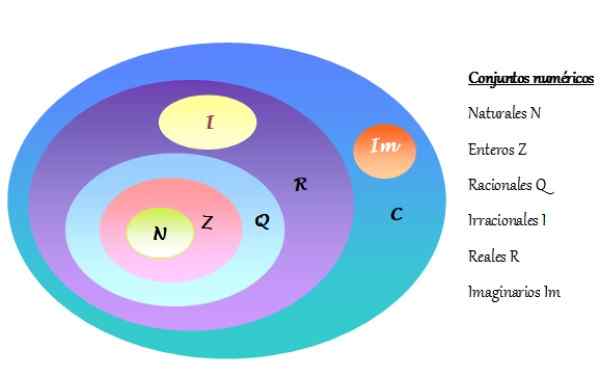
-Kompleksilukujen joukko on merkitty C: ksi ja sisältää reaalilukut r ja kuvitteelliset numerot Im. Numeeriset sarjat on esitetty Venn -kaaviossa, kuten seuraavassa kuvassa esitetään:

Voi palvella sinua: ratkaistu tekijäharjoitukset Kuva 2. Venn -kaavio numeerisista sarjoista. Lähde: f. Zapata.

-Jokainen kompleksi numero koostuu yhdestä todellisesta osasta ja toisesta kuvitteellisesta osasta.

-Kun kompleksinumeron kuvitteellinen osa on 0, se on puhdas reaaliluku.

-Jos kompleksinumeron todellinen osa on 0, niin numero on puhdas kuvitteellinen.

-Kaksi kompleksia ovat samat, jos niiden oikea osa ja kuvitteellinen osa ovat samat.

-Kompleksilukujen avulla suoritetaan summien, vähennys-, kertolasku-, tuotteiden ja vaikutusmahdollisuuksien toiminnot, mikä johtaa toiseen kompleksilukuun.

Kompleksilukujen esitys

Monimutkaiset numerot voidaan edustaa eri tavoin. Tässä ovat tärkeimmät:

- Binominen muoto

Se on annettu muoto alussa, missä z -z on kompleksinumero, -lla on todellinen osa, b - on kuvitteellinen osa ja Yllyttää Se on kuvitteellinen yksikkö:

Z = A + IB

Tai myös:

Z = x + iy

Yksi tapa piirtää kompleksinumero on tässä kuvassa esitetyn kompleksitason kautta. Kuvitteellinen akseli on pystysuora, kun taas todellinen akseli on vaakasuora ja merkitsee.

Kompleksinumero z -z Se on esitetty tässä tasossa koordinaattipisteinä (X, y) jompikumpi (A, b), Kuten todellisen lentokoneen pisteillä tehdään.

Etäisyys alkuperästä pisteeseen Z on kompleksinumeron moduuli, joka on merkitty r -, kun taas φ on kulma, joka muodostuu r - Oikealla akselilla.

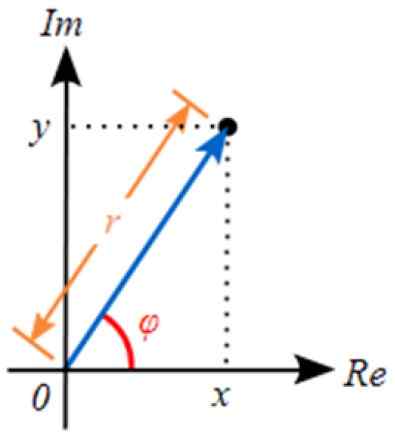
Kuva 3. Kompleksinumeron esitys kompleksissa. Lähde: Wikimedia Commons.

Tämä esitys liittyy läheisesti todellisen tason vektorien esitykseen. R: n arvo vastaa moduuli kompleksinumero.

Se voi palvella sinua: Gauss-Seidel-menetelmä: Selitys, sovellukset, esimerkit

- Napainen muoto

Polaarinen muoto koostuu kompleksilukujen ilmaisemisesta, jotka antavat arvot r - ja φ. Jos tarkastelemme kuvaa, arvo r - Se vastaa oikean kolmion hypotenusia. Luokat ovat arvoisia -lla ja b -, O hyvin x ja ja.

Binomiaalisessa tai binomimuodossa voimme siirtyä polaariseen muotoon:

R = √x²+ja²

Kulma φ Se muodostaa R -segmentin vaaka -akselilla tai kuvitteellisella akselilla. Se tunnetaan nimellä Perustelu kompleksinumero. Tällä tavalla:

φ = arctg (y/x)

Argumentilla on äärettömät arvot, ottaen huomioon. Tällä tavalla yleensä Z: n arg (z) -argumentti ilmaistaan ​​seuraavasti:

Arg (z) = φ + 2kπ

Missä K on kokonainen ja osoittaa käännettyjen käännösten määrän: 2, 3, 4 .. . Merkki osoittaa pyörimisen merkityksen, jos aika tai antihorario tehdään.

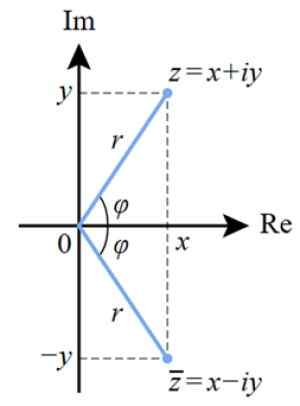
Kuva 4. Kompleksinumeron polaarinen esitys kompleksissa. Lähde: Wikimedia Commons.

Ja jos haluamme siirtää polaarisen muodon binomimuotoon, käytämme trigonometrisiä syitä. Edellisestä kuvasta voimme nähdä sen:

x = r cos φ

y = r sen φ

Tällä tavalla z = r (cos φ+i sin φ)

Se on lyhennetty näin:

z = r cis φ

Esimerkkejä monimutkaisista numeroista

Seuraavat kompleksilukut annetaan binomiaalisesti:

a) 3 + I

b) 4

d) -6i

Ja nämä järjestetyssä vääntömomentissa:

a) (-5, -3)

b) (0, 9)

c) (7,0)

Lopuksi, tälle ryhmälle annetaan polaarista tai trigonometristä:

a) √2 cis 45º

b) √3 cis 30º

Voi palvella sinua: hypergeometrinen jakauma: kaavat, yhtälöt, malli

c) 2 cis 315º

Mihin tarkoitukseen ne ovat?

Kompleksilukujen hyödyllisyys ylittää alussa esitetyn toisen asteen yhtälön resoluutiota, koska ne ovat välttämättömiä tekniikan ja fysiikan alalla, etenkin:

-Sähkömagneettisten aaltojen tutkimus

-Vaihtoehtoinen virta- ja jänniteanalyysi

-Kaikenlaisten signaalien mallintaminen

-Suhteellisuusteoria, jossa ajan oletetaan kuvitteellisena suuruutena.

Toiminnot monimutkaisilla numeroilla

Monimutkaisten numeroiden avulla voimme suorittaa kaikki toiminnot, jotka tehdään oikealla. Jotkut ovat helpompaa tehdä, jos numerot tulevat binomisesti, kuten summa ja vähennys. Toisaalta kertolasku ja jako ovat yksinkertaisempia, jos ne suoritetaan polaarimuodolla.

Katsotaanpa joitain esimerkkejä:

- Esimerkki 1

Lisää z₁ = 2 + 5i ja Z₂ = -3 -8i

Ratkaisu

Oikeat osat lisätään erikseen kuvitteellisista osista:

z -z₁ + z -z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Esimerkki 2

Kerro z₁ = 4 cis 45º ja z₂ = 5 cis 120º

Ratkaisu

Voidaan osoittaa, että kahden kompleksinumeron tuote polaarisessa tai trigonometrisessä on annettava:

z -z₁ . z -z₂ = r₁.r -₂ Cis (φ₁ + φ₂-A

Tämän perusteella:

z -z₁ . z -z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Soveltaminen

Kompleksilukujen yksinkertainen sovellus on löytää kaikki polynomiyhtälön juuret, kuten artikkelin alussa esitetty.

Yhtälön X tapauksessa² - 10x + 34 = 0, kun se on saatu liuotinkaavaa:

Siksi ratkaisut ovat:

x₁ = 5 + 3i

x₂ = 5 - 3i

Viitteet

1. Earl, r. Kompleksilukut. Toipunut: matematiikka.härkä.Ac.Yhdistynyt kuningaskunta.
2. Figuera, J. 2000. 1. matematiikka. Monipuolinen. Co-bo-painikkeet.
3. Hoffmann, J. 2005. Matematiikan aiheiden valinta. Monfort -julkaisut.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Kompleksilukut. Haettu: vuonna.Wikipedia.org