Ominaisuudet Prime -numerot, esimerkit, harjoitukset

Se alkuluvut, Kutsutaan myös absoluuttisia serkkuja, ovat luonnollisia lukuja, jotka ovat vain jaettavissa toistensa kanssa ja 1. Tässä luokassa numerot, kuten: 2, 3, 5, 7, 11, 13, 17, 19, 23 ja monet muut tulevat tähän luokkaan.

Toisaalta yhdistelmänumero on jaettavissa itsessään, yhdellä ja ainakin yhä vielä yksi numero. Meillä on esimerkiksi 12: lla, mikä on jaettavissa 1, 2, 4, 6 ja 12. Kokouksen mukaan 1.

Kuvio 1. Joitakin alkulukuja. Lähde: Wikimedia Commons.

Alkeislukujen tuntemus on peräisin etäaikoista; Muinaiset egyptiläiset jo käsittelivät heitä ja olivat varmasti tiedossa kauan ennen.

Nämä luvut ovat erittäin tärkeitä, koska mitä tahansa luonnollista lukua voidaan edustaa päälukujen tuote, joka on tämä ainutlaatuinen esitys, paitsi tekijöiden järjestyksessä.

Tämä tosiasia on täysin vakiintunut lauseeseen nimeltään Aritmeettisen peruslause, joka toteaa, että serkkujen lukumäärät koostuvat välttämättä numeroista, jotka ovat.

[TOC]

Alkeislukujen ominaisuudet

Alkeislukujen pääominaisuuksien alapuolella:

-Ne ovat äärettömiä, koska kuitenkin suuria prime -lukuja löytyy aina.

-Jos pääluku p ei jaa tarkalleen toiseen numeroon -lla, Sitten sanotaan, että p ja -lla He ovat serkkuja keskenään. Kun tämä tapahtuu, ainoa yleinen jakaja on 1.

Se ei ole välttämätöntä -lla Olla absoluuttinen serkku. Esimerkiksi 5 on serkku, ja vaikka 12 ei ole, molemmat numerot ovat serkkuja keskenään, koska kahdella on yhteinen jakaja 1.

-Kun pääluku p jaa numeron voima n, Se jakaa myös a n. Harkitse 100, joka on 10, erityisesti 10, 10². Tapahtuu, että 2 jakaa sekä 100 että 10.

-Kaikki pääluvut ovat parittomia lukuun ottamatta 2, joten niiden viimeinen numero on 1, 3, 7 tai 9. 5 ei ole mukana, koska vaikka se on outoa ja serkkua, se ei ole koskaan toisen päämäärän lopullinen luku. Itse asiassa kaikki numerot, jotka päättyvät viidessä, ovat tämän kerrannaisia, eivätkä siksi ole serkkuja.

Voi palvella sinua: Keskeinen symmetria: Ominaisuudet, esimerkit ja harjoitukset

-Joo p Se on kahden numeron serkku ja jakaja -lla.b -, niin p Jaa yksi heistä. Esimerkiksi ensisijainen numero 3 jakaa tuotteen 9 x 11 = 99, koska 3 on jakaja 9.

Kuinka tietää, onko numero serkku

Se Ensisijaisuus Se on serkkun laatuun annettava nimi. No, ranskalainen matemaattinen Ferman pieni lause, Se sanoo niin:

"Annetaan serkku luonnollinen luku p ja mikä tahansa luonnollinen numero -lla suurempi kuin 0, se täyttyy -lla^p - -lla Se on useita p, niin kauan kuin p olla serkku ".

Voimme vahvistaa tämän käyttämällä pieniä numeroita, esimerkiksi P = 4, että tiedämme jo, että se ei ole serkku ja A = 6:

6⁴ - 6 = 1296 - 6 = 1290

Numero 1290 ei ole tarkalleen jaettavissa 4: n välillä, joten 4 ei ole alkuluku.

Tehdään nyt testi p = 5: llä, joka on serkku ja A = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 on jaettavissa 5: n välillä, koska mikä tahansa lukumäärä 0 tai 5 on. Itse asiassa 7760/5 = 1554. Kun Fermatin pieni lause täyttyy, voimme varmistaa, että 5 on ensisijainen numero.

Lauseen kautta oleva testi on tehokas ja suora pienillä numeroilla, joissa operaatio on helppo suorittaa, mutta mitä tehdä, jos he pyytävät meitä selvittämään suuren määrän ensisijaisuus?

Tällöin lukumäärä on jaettu peräkkäin kaikkien pienten päälukujen kesken, kunnes tarkka jako tai että osamäärä on pienempi kuin jakaja.

Jos jokin jako on tarkka, se tarkoittaa, että numero on yhdiste ja jos osamäärä on pienempi kuin jakaja, se tarkoittaa, että luku on serkku. Lyhyt sen käytännössä vuonna ratkaisi 2.

Tapoja löytää ensisijainen numero

Alkeislukuja on ääretön, eikä niiden määrittämistä ei ole ainutlaatuista kaavaa. Joidenkin tällaisten alareunojen havaitseminen:

Voi palvella sinua: NULL Kulma: Määritelmä ja ominaisuudet, esimerkit, harjoitukset

3, 7, 31, 127 ..

Havaitaan, että ne ovat muodossa 2ⁿ - 1, n = 2, 3, 5, 7, 9 ... vakuutamme sinulle:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Mutta emme voi vakuuttaa sitä yleensä 2ⁿ - 1 olla serkku, koska on joitain arvoja n jolle se ei toimi, esimerkiksi 4:

2⁴ - 1 = 16 - 1 = 15

Ja numero 15 ei ole serkku, koska se päättyy 5. Kuitenkin yksi suurimmista päälukuista, jotka tunnetaan tietokonevalmisteilla, on kuitenkin muodossa 2ⁿ - 1 kanssa:

N = 57.885.161

Se Mersenne -kaava vakuuttaa meille, että 2^p - 1 on aina serkku, niin kauan kuin p Olla myös serkku. Esimerkiksi 31 on serkku, joten on varmaa, että 2³¹ - 1 Se on myös:

2³¹ - 1 = 2.147.483.647

Kaava sallii kuitenkin vain joidenkin alareunojen määrittämisen, ei kaikki.

Eulerin kaava

Seuraava polynomi mahdollistaa ensisijaisten numeroiden löytämisen niin kauan kuin N on välillä 0 - 39:

P (n) = n² + N + 41

Myöhemmin ratkaistuissa harjoitusosassa on esimerkki sen käytöstä.

Eratostenes -seulonta

Eratóstenes oli muinaisen Kreikan fysiikka ja matemaattinen, joka asui kolmannella vuosisadalla.C. Hän suunnitteli graafisen menetelmän löytääkseen alusluvut, jotka voimme käyttää käytännössä pienillä numeroilla, sitä kutsutaan Eratóstenes -näyttöksi (näyttö on kuin suodatin).

-Numerot sijoitetaan animaation kaltaiseen taulukkoon.

-Sitten parilliset numerot on merkitty, paitsi 2, jotka tiedämme olevan serkku. Kaikki muut ovat tämän kerrannaisia, ja siksi he eivät ole serkkuja.

-Myös 3, 5, 7 ja 11 -kertoimet on merkitty, lukuun ottamatta niitä kaikkia, koska tiedämme, että ne ovat serkkuja.

-4, 6, 8, 9 ja 10 kertoimet on jo merkitty, koska ne ovat yhdisteitä ja siksi minkä tahansa ilmoitetun serkku.

Voi palvella sinua: trigonometrian historia sen alkuperästä

-Lopuksi, jäljellä olevat numerot ovat merkitsemättömiä serkkuja.

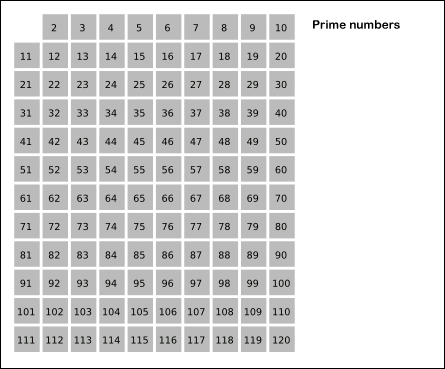Kuva 2. Eratostenes -seulonta -animaatio. Lähde: Wikimedia Commons.

Harjoitukset

- Harjoitus 1

Löydä 3 numeroa yli 100 käyttämällä euler -polynomia aluslukuille.

Ratkaisu

Tämä on polynomi, jonka Euler ehdotti ensisijaisten lukujen löytämistä, joka toimii N -arvoilla välillä 0 - 39.

P (n) = n² + N + 41

Tanteon kautta valitsemme arvon n, esimerkiksi n = 8:

P (8) = 8² + 8 + 41 = 113

Koska n = 8 tuottaa alkuluvun yli 100, arvioimme polynomia n = 9 ja n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Harjoitus 2

Ota selvää, ovatko seuraavat numerot serkut:

a) 13

b) 191

Liittää jhk

13 on riittävän pieni käyttämään Fermatin pientä lauseita ja laskimen apua.

Käytämme A = 2 niin, että numerot eivät ole liian suuria, vaikka niitä voidaan käyttää myös A = 3, 4 tai 5:

2¹³ - 2 = 8190

8190 on jaettavissa 2: n välillä, koska se on tasainen, siksi 13 on serkku. Lukija voi vahvistaa sen tekemällä saman testin a = 3: lla.

Ratkaisu b

191 on erittäin suuri kokeilemaan lausetta ja yhteistä laskinta, mutta voimme suorittaa jaon kunkin päämäärän välillä. Me jätämme jakamaan 2: lla, koska 191 ei ole edes ja jako ei ole tarkka tai suhde alle 2.

Yritimme jakaa 3:

191/3 = 63 666…

Ja se ei anna tarkkaa, eikä osamäärä ole pienempi kuin jakaja (63 666 ... on suurempi kuin 3)

Jatkamme serkkujen 5, 7, 11, 13 testaamisen 191 testaamista ja tarkkaa jakautumista ei saavuteta, eikä suhde pienempi kuin jakaja. Kunnes se jakaa välillä 17:

191/17 = 11, 2352 ..

Koska se ei ole tarkka ja 11 2352 ... se on alle 17, numero 191 on serkku.

Viitteet

1. Baldor, a. 1986. Aritmeettinen. Codex -versiot ja jakaumat.
2. Prieto, c. Primo -numerot. Haettu: sivut.Matem.Yksinäinen.MX.
3. Alkeislukujen ominaisuudet. Toipunut: Mae.UFL.Edu.
4. Älykkyys. Primo -numerot: Kuinka löytää ne Eratostenesin seulan kanssa. Toipunut: Smartck.On.
5. Wikipedia. alkuluku. Palautettu: on.Wikipedia.org.