Kokonaisluvut

Mitkä ovat kokonaiset numerot?

Kokonaisluvut muodostavat joukon hyödyllisiä numeroita, jotta voidaan laskea kokonaiset objektit, joita on ja niitä, jotka eivät ole. Myös tietyn viitepaikan toisella puolella ja toisella puolella.

Myös kokonaislukujen kanssa vähennys tai ero voidaan suorittaa lukumäärän ja toisen suuremman kuin hän, joka on ratkaistu, esimerkiksi velkaa, esimerkiksi velkaa. Voittojen ja velkojen ero on vastaavasti merkinnöillä + ja -.

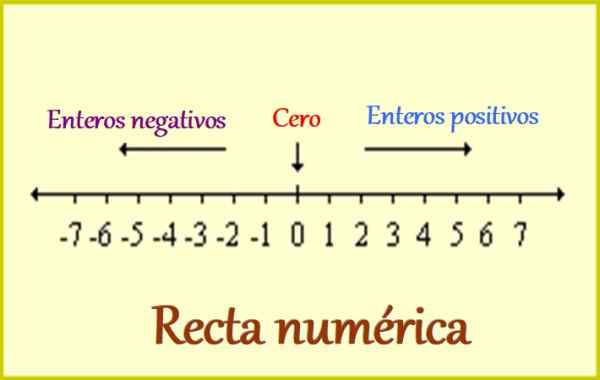
Kuvio 1. Kokonaislukujen numeerinen viiva. Lähde: Wikimedia Commons. Leomg/cc by-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0).

Siksi koko numerot sisältävät seuraavat:

-Positiiviset kokonaisluvut, joita on kirjoitettu A +. Esimerkiksi: +1, +2, +3 ... ja niin edelleen.

-0, jossa merkkiä ei ole merkityksetön, koska se ei lisää sitä vähentämään sitä jostakin määrästä. Mutta 0 on erittäin tärkeä, koska se on kokonaislukujen viite: toisella puolella positiiviset sijaitsevat ja negatiivit, kuten ylemmässä kuvassa näemme.

-Negatiiviset kokonaisluvut, jotka on aina kirjoitettava merkistä -koska heidän kanssaan määrät, kuten velat ja kaikki viitteen toisella puolella olevat, erottuvat. Esimerkkejä negatiivisista kokonaislukuista ovat: -1, -2, -3 ... ja siitä lähtien.

Kuinka kokonaiset numerot ovat?

Alussa edustavat koko numeroa sarjan asettamalla: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, ts. listattu ja järjestetty. Mutta erittäin hyödyllinen esitys on se, mikä käyttää numeerista linjaa. Tätä varten on välttämätöntä piirtää viiva, joka on yleensä vaakasuora, jolle 0 on merkitty ja jaettu identtisiin osiin:

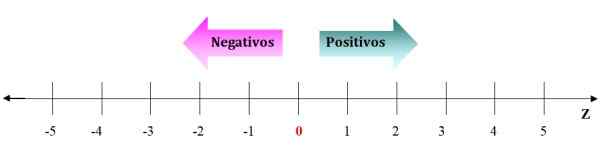Kuva 2. Kokonaislukujen esitys numeerisella viivalla. 0: sta oikealle ovat positiiviset kokonaisluvut ja 0 vasemmalle negatiiviset. Lähde: f. Zapata.

Negatiivit menevät vasemmalle 0: sta ja positiiviset menevät oikealle. Numerorivin nuolet symboloivat, että numerot jatkavat äärettömyyttä. Kunkin kokonaisluvun vuoksi on aina mahdollista löytää sellainen, joka on suurempi tai muu kuin alempi.

Kokonaisluvun absoluuttinen arvo

Kokonaisluvun absoluuttinen arvo on lukumäärän ja 0 välinen etäisyys. Ja etäisyydet ovat aina positiivisia. Siksi negatiivisen kokonaisluvun absoluuttinen arvo on luku ilman sen merkkiä vähemmän.

Esimerkiksi absoluuttinen arvo -5 on 5. Absoluuttinen arvo on merkitty baareilla, seuraavasti:

| -5 | = 5

Sen visualisoimiseksi riittää, että tilat ovat numeerisella viivalla, -5 -0. Vaikka positiivisen kokonaisluvun absoluuttinen arvo on sama luku, esimerkiksi | +3 | = 3, koska sen etäisyys 0: een on 3 tilaa:

Voi palvella sinua: Sandwich Law: Selitys ja harjoitukset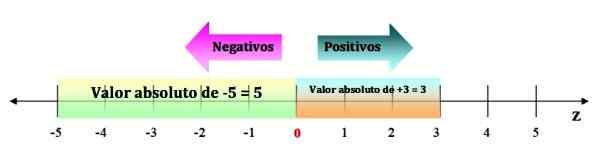Kuva 3. Kokonaisluvun absoluuttinen arvo on aina positiivinen määrä. Lähde: f. Zapata.

Ominaisuudet

-Kokonaislukujoukko on merkitty z: ksi ja sisältää luonnonlukujen n, niiden elementit ovat äärettömiä.

-Kokonaisluku ja se, joka seuraa (tai sitä edeltävä), eroaa aina yksikössä. Esimerkiksi sen jälkeen kun 5 tulee 6, koska se on 1 ero niiden välillä.

-Jokaisessa kokonaisluvussa on edeltäjä ja seuraaja.

-Mikä tahansa positiivinen kokonaisluku on suurempi kuin 0.

-Negatiivinen kokonaisluku on aina alle 0 ja mikä tahansa positiivinen luku. Otetaan esimerkiksi numero -100, tämä on alle 2, kuin 10 ja 50. Mutta se on myös alle -10, -20 ja -99 ja se on yli -200.

-0: lla ei ole merkin näkökohtia, koska se ei ole negatiivinen tai positiivinen.

-Koko numeroiden kanssa voidaan suorittaa samat operaatiot, jotka suoritetaan luonnollisilla lukuilla, nimittäin: summa, vähennys, kertolasku, potentiaatio ja paljon muuta.

-Koko vastakohta tiettyyn kokonaislukuun X on -x ja kokonaisluvun summa sen vastakkaisella on 0:

x + (-x) = 0.

Toiminnot, joissa on kokonaiset numerot

- Lisäys

-Jos lisättävillä numeroilla on sama merkki, niiden absoluuttiset arvot lisätään ja tulos on sijoitettu merkki, jonka lisäys on. Tässä on joitain esimerkkejä:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-Jos numerot ovat eri merkkejä, absoluuttiset arvot (alaikäisten pääosat) vähennetään ja tulos on sijoitettu lukumäärästä, jolla on korkein absoluuttinen arvo, seuraavasti:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Kokonaislukujen summan ominaisuudet

-Summa on kommutatiivinen, joten lisäysjärjestys ei muuta summaa. Olkoon A ja B kaksi kokonaisluku, on täytetty, että a+b = b+a

-0 on kokonaislukujen summan neutraali elementti: a + 0 = a

-Mikä tahansa sen vastakkaisella lisätty kokonainen numero on 0. + A: n vastakohta on -a ja päinvastoin -a -A ES + A. Siksi: (+ a)+ (-a) = 0.

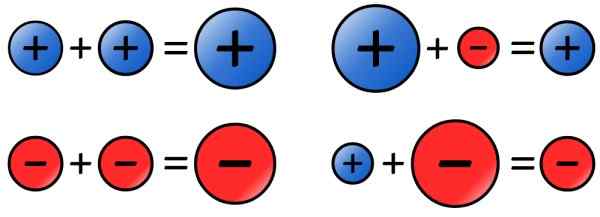Kuva 4. Merkitsee sääntöä kokonaislukujen summalle. Lähde: Wikimedia Commons.

- Vähennyslasku

Kokojen lukujen vähentämiseksi sinun on ohjattava tämä sääntö: Vähennys vastaa numeron summaa vastakkaisella. Anna sitten kaksi numeroa A ja B, sitten:

A - B = A + (-b)

Oletetaan esimerkiksi, että sinun on tehtävä seuraava toimenpide: (-3) - (+7), sitten:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Kertolasku

Kokonaislukujen kertominen noudattaa tiettyjä merkkejä koskevia sääntöjä:

-Kahden numeron tuote Sama merkki Se on aina positiivinen.

-Kun kaksi lukua moninkertaistuu eri merkit, Tulos on aina negatiivinen.

Voi palvella sinua: mitkä ovat osan osia? (Esimerkkejä)

-Tuotteen arvo on yhtä suuri kuin vastaavien absoluuttisten arvojen kertominen.

Heti joitain esimerkkejä, jotka selventävät yllä:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Kokonaislukujen kertolaskujen ominaisuudet

-Kertolasku on kommutatiivista. Ole kaksi kokonaislukua a ja b, on totta, että: a.B = b.A, joka voidaan myös ilmaista seuraavasti:

Tekijöiden järjestys ei muuta tuotetta.

-Kertolaskun neutraali elementti on 1. Olla siis kokonaisluku.1 = 1

-Jokainen kokonaisluku kerrottuna 0: lla on yhtä suuri kuin 0: a.0 = 0

Jakautuva omaisuus

Kertolasku täyttää jakavan omaisuuden summan suhteen. Kyllä A, B ja C ovat sitten kokonaisia ​​numeroita:

-lla.(b +c) = a.b + a.c

Sitten esimerkki tämän ominaisuuden soveltamisesta:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Potentiaatio

-Jos pohja on positiivinen, operaation tulos on aina positiivinen.

-Kun emäs on negatiivinen, jos eksponentti on tasainen, tulos on positiivinen. Ja jos eksponentti on outoa, tulos on negatiivinen.

- Jako

Divisioonassa samoja merkintösääntöjä sovelletaan kuin kertolasku:

-Jakamalla kaksi saman merkin kokonaislukua, tulos on aina positiivinen.

-Kun kaksi eri merkin kokonaislukua on jaettu, osamäärä on negatiivinen.

Esimerkiksi:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Tärkeä: Jako ei ole kommutatiivinen, toisin sanoen ÷ b ≠ b ÷ a ja kuten aina, jaon 0 välillä ei ole sallittua.

- Potentiaatio

Ole kokonaismäärä ja haluamme nostaa sen eksponentti N: lle, niin meidän on kerrottava itse, kuten alla on esitetty:

-llaⁿ = a.-lla.-lla.-lla.…

Tarkastellaan myös seuraavaa ottaen huomioon, että n on luonnollinen numero:

-Jos a on negatiivinen ja n on tasainen, tulos on positiivinen.

-Kun a on negatiivinen ja n on pariton, se johtaa negatiiviseen lukumäärään.

-Jos A on positiivinen ja n on tasainen tai pariton, se on aina positiivinen kokonaisluku.

-Mikä tahansa kokonaisluku, joka on korotettu 0: een, on yhtä suuri kuin 1: a^{0 -} = 1

-Jokainen lukumäärä 1 on yhtä suuri kuin luku: a¹ = a

Otetaan esimerkiksi löytää (-3)⁴ , Jotta se kertoo (-3) neljä kertaa itsestään, kuten näin: (-3).(-3).(-3).(-3) = 81.

Toinen esimerkki, myös negatiivisella kokonaisluvulla on:

(-2)³ = (-2).(-2).(-2) = -8

Tasavertaiset perusvoimat

Oletetaan, että kaksi yhtä suurta emäksistä voimaa, jos kerrotaan ne, saamme uuden voiman saman pohjan kanssa, jonka eksponentti on annetun eksponentin summa:

-llaⁿ ·^m = a^{n + m}

Yhtä suuri jauhesuhde

Jakamalla saman pohjan voimat, tulos on voima, jolla on sama pohja, jonka eksponentti on annetun eksponentin vähentäminen:

Voi palvella sinua: kehän kulmat: tyypit, ominaisuudet, ratkaistut harjoitukset

-llaⁿ ÷ a^m = a^{n - m}

Sitten kaksi esimerkkiä, jotka selventävät näitä kohtia:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Esimerkit

Tarkastellaan yksinkertaisia ​​esimerkkejä näiden sääntöjen soveltamiseksi muistettaessa, että positiivisten kokonaislukujen tapauksessa merkki voidaan luopua:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

H) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Ratkaisut

- Harjoitus 1

ANT liikkuu kuvan 1 numeroviivalla. Alkaen pisteestä x = +3 suorittaa seuraavat siirtymät:

-7 yksikköä siirtyy oikealle

-Nyt 5 yksikköä palautetaan vasemmalle

-Kävele 3 yksikköä vasemmalle.

-Se palaa ja siirtää 4 yksikköä oikealle.

Missä vaiheessa muurahainen reitin lopussa?

Ratkaisu

Kutsutaan siirtymät. Kun he ovat oikealla puolella, heille annetaan positiivinen merkki ja kun he ovat vasemmalla negatiivisella merkkillä. Tällä tavalla ja alkaen x = +3 sinulla on:

-Ensimmäinen d: x₁ = +3 +7 = +10

-Toinen D: x₂ = +10 +(-5) = +5

-Kolmas d: x₃ = +5 +(-3) = +2

-Neljäs d: x₄ = +2 +4 = +6

Kun muurahainen päättyy, sen kävely on asennossa x = +6. Eli se on 6 yksikköä oikealla puolella 0 numeerisella viivalla.

- Harjoitus 2

Ratkaise seuraava toimenpide:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Ratkaisu

Tämä operaatio sisältää merkkejä ryhmittelystä, jotka ovat suluista, neliömäisistä suluista ja avaimista. Ratkaistuasi sinun on ensin huolehdittava suluista, neliömäisten kiinnikkeiden ja lopulta avaimien jälkeen. Toisin sanoen sinun on työskenneltävä sisältäpäin.

Tässä harjoituksessa piste edustaa kertolaskua, mutta jos yhden numeron ja sulkujen tai muun symbolin välillä ei ole mitään järkeä, samalla tavalla kuin ymmärretään, että se on tuote.

Seuraavaksi resoluutio askel askeleelta värit toimivat ohjeena sulujen vähentämisen tuloksen seuraamiseksi, jotka ovat sisäisimpiä ryhmän symboleja:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1-4] = 52.-3 = -156

- Harjoitus 3

Ratkaise ensimmäisen asteen yhtälö:

12 + x = 30 + 3x

Ratkaisu

Ehdot on ryhmitelty tasa -arvon vasemmalla puolella ja oikealla olevilla numeerisilla termeillä:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9