Merkinnät kehittivät esimerkkejä ja harjoituksia
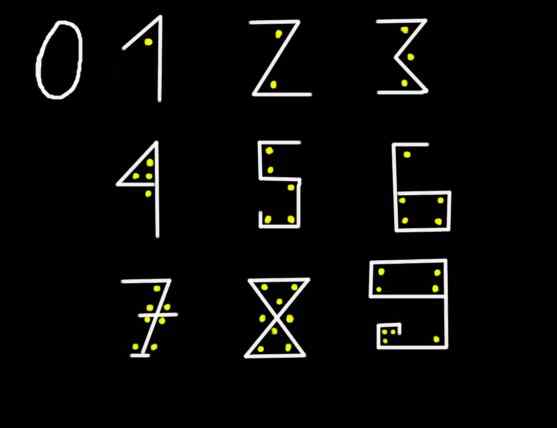
- 3010
- 539
- Edgar VonRueden
Se Kehitetty merkintä Se on sellainen, jossa numeerinen luku ilmaistaan summana, jossa lukumäärän muodostavan numeron sijaintiarvo otetaan huomioon.
Esimerkiksi, kun kirjoitat lukua 2345, jokaisella numerolla on paikallinen hierarkia. Oikean äärimmäisen numeron lukeminen vasemmalle, hierarkia tai arvo kasvaa.
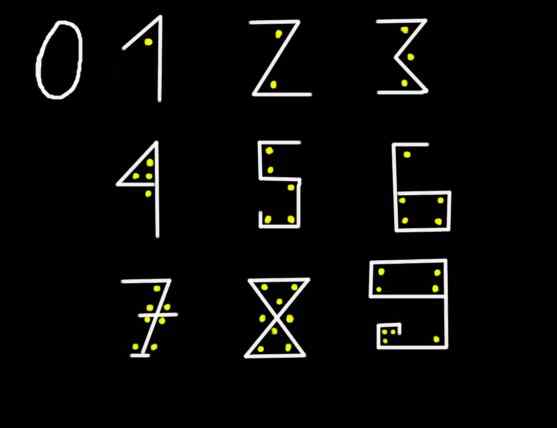 Kuvio 1. Yhdeksällä grafemilla on mahdollista edustaa mitä tahansa lukua.
Kuvio 1. Yhdeksällä grafemilla on mahdollista edustaa mitä tahansa lukua. Kuviossa 2345 numero 5 edustaa viittä yksikköä, numero 4 edustaa neljää kymmeniä, 3 vastaa kolmatta sijaintia vasemmalta oikealle ja siksi 3 edustaa kolmea sataa, lopulta 2 edustaa kahta tuhatta. Eli kehittyneessä tai laajennetussa merkinnässä kuva 2345 on kirjoitettu näin:
2345 = 2 tuhatta + 3 sataa + 4 kymmeniä + 5 yksikköä
Mutta se voidaan myös ilmaista seuraavasti:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Kuva 2345 voidaan kirjoittaa myös 10: n voiman summana:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Missä ympärysjoukko ^ tarkoittaa ilmoitetun eksponentin nostamista. Esimerkiksi 10^3 = 10 x 10 x 10 = 1000. Toinen tapa kirjoittaa eksponentteja on valvonta:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100 -
[TOC]
Paikannusjärjestelmä
Arabialukujärjestelmä ovat lukuja, joita käytetään päivittäin suurimmassa osassa mantereita ja maista maailmassa. Arabialuvut ovat perusjärjestelmä 10, koska kymmenen symbolia tai grafemaa käytetään minkä tahansa numeron kirjoittamiseen. Nämä kymmenen symbolia ovat:
0 1 2 3 4 5 6 7 8 9
Vain yhdellä näistä symboleista, nollasta yhdeksään välillä voidaan ilmaista. Yli yhdeksän lukujen ilmaisemiseksi, kymmeneen perustuva sijaintijärjestelmä. Kuva 10 on tusina ja nolla yksikköä. Kuva 11 on tusina ja yksikkö. Kuva 123 (sata kaksikymmentäkolme) on sata, kaksi kymmeniä ja kolme yksikköä. Kymmenen voiman muodossa kirjoitettu numero 123 on:
Voi palvella sinua: 60 jakajaa1 × 10^2 + 2 × 10^1 + 3 × 10^0
Missä:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Tämän esimerkin avulla on selvää, että numeron sijainti lopussa on sijainti 0 ja edustaa yksiköiden lukumäärää, toisen numeron sijainti oikealta vasemmalle on sijainti 1 ja edustaa kymmenien lukumäärää, kolmas numero (oikealle toiseen vasemmalla) on sijainti 2 ja se edustaa satoja.
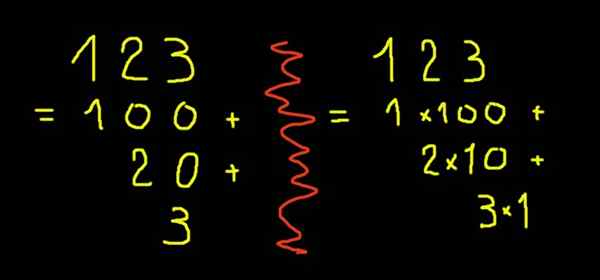 Kuva 2. Kehitetty merkintä kuviosta 123.
Kuva 2. Kehitetty merkintä kuviosta 123. Murto- tai desimaalilukuja
Desimaalin sijaintijärjestelmän kanssa se on myös mahdollista.
Edustaaksesi fraktiota ½ arabialaisessa desimaalijärjestelmässä, ts. Puolet yksiköstä on kirjoitettu:
½ = 0,5
Tämän lausekkeen saavuttamiseksi järjestelmässämme 10: n perusteella on tehty seuraavat toiminnot:
1- Kerrota numeroija ja nimittäjä 5: lle, jos vastaava fraktio 5/10 = 1/2.
2- Jaa 10: llä vastaa kertomista teholla, joka perustuu kymmeneen eksponentin vähemmän (10^-1), eli 5/10 = 5 × 10^-1.
3- Negatiivinen eksponentti osoittaa, kuinka monta kertaa yksikön sijainnista osoitettu numero ajetaan tai sijoitetaan, meidän tapauksessamme se olisi 0,5.
4- ½ = 0,5 laajennetussa merkinnässä se on kirjoitettu näin:
0,5 = 0x10^0 + 5 × 10^-1
Missä 10^-1 = 0,1 on kymmenesosa (osuus yksikköä vastaa 10 yhtä suurta osaa).
Tällä tavalla luku 0,5 vastaa viittä kymmenesosaa, mutta luku 0,05 vastaa 5 sataa ja 0,005 - 5 tuhatta.
Voi palvella sinua: Miksi algebra on tärkeä tietyissä päivittäisessä tilanteessa?Kehitetty merkinnät esimerkkejä
Esimerkki 1
Kun otetaan huomioon tavanomaisen merkinnän 40201 -kuva, muunna se kehitettyksi merkinnäksi.
Ratkaisu:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Esimerkki 2
Kirjoita murto ¾ pidennetyllä merkinnällä.
Ratkaisu:
Tässä tapauksessa yksiköstä on kolme neljäsosaa.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Sanoisesti sanottu olisi näin:
Jake ¾ vastaa seitsemää kymmenesosaa ja viisi sataa.
Kehitetyt merkintäharjoitukset
Harjoitus 1
Sano sanoissa.
Ratkaisu:
Kehitetty merkintä on tällainen:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Että sanan kielellä sanotaan:
Neljä kymmeniä tuhansia, plus tuhansia, plus kaksisataa, enemmän nolla kymmeniä sekä yksikkö.
Harjoitus 2
Ilmaise sanoja edellisessä kuvassa ja hajota vastaava kehitetty lause.
Ratkaisu:
Sanoin 40201 -kuva ilmaistaan seuraavasti:
Neljäkymmentätuhatta kaksisataa yksi
Aikaisempi lause voi kehittyä seuraavasti:
40 × 1000 + 2 × 100 + 1
Voidaan sanoa, että tapa lausua lukuja on puoliksi kehittynyt tapa ilmaista se.
Harjoitus 3
Kirjoita numero 7/3 kehitetty tapa.
Ratkaisu:
Se on luku, joka ilmaistaan virheellisenä fraktiona, koska koska osoitin on suurempi kuin nimittäjä, luku on suurempi kuin yksikkö.
Tämä virheellinen osuus voidaan hajottaa, kun fraktioiden summa 6/3 + 1/3. Ensimmäinen fraktioista johtaa kokonaisluku 2, kun taas 1/3 = 0,333333, jossa numero 3 toistetaan toistaiseksi. Niin, että 7/3 -kuvion kehitetty desimaalimyrsky on aina likimääräinen lauseke:
Voi palvella sinua: nelikulmainen: elementit, ominaisuudet, luokittelu, esimerkit7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Harjoitus 6
Kirjoita vakiomerkinnässä ja kehitä sitten numero: Kaksikymmentäkolme miljardia kaksisataa ja viisikymmentä miljoonaa viisisataa kaksikymmentä -kuusi tuhatta kolmesataa kaksikymmentä -viisi kolmella kaksikymmentäkolme tuhannesosaa.
Ratkaisu:
On muistettava, että a Millardo vastaa miljardia. Sana Millardo Espanjan kuninkaallinen akatemia hyväksyi sen vuonna 1995 Venezuelan myöhäisen presidentin Rafael Calderan, Venezuelan kieliakatemian jäsenen pyynnöstä. Tällöin vakiomerkinnän luku kirjoitetaan seuraavasti:
23.2501526.325 023
23 miljardia + 250 miljoonaa + 526 tuhatta + 325 yksikköä + 23 tuhatta.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Lopuksi kirjoitetaan kehitetyn merkinnän luku:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Viitteet
- Khan -akatemia. Sijainti -arvotaulukot. Palautettu: on.Khanacademy.org
- Khan -akatemia. Kirjoita kehitetty numero (video). Palautettu: on.Khanacademy.org
- Ifrah, Geoges (1998): Lukujen yleinen historia. Espasa calpe s.-Lla.
- Wikipedia. Sijainti. Palautettu: on.Wikipedia.com
- Wikipedia. Millardo. Palautettu: on.Wikipedia.com
- « Fosforioksidi (V) rakenne, ominaisuudet, hankkiminen, käyttö, riskit
- Alumiinifosfaatti (ALPO4) rakenne, ominaisuudet, hankkiminen, käyttö »

