Hyperbolinen paraboloidi määritelmä, ominaisuudet ja esimerkit

Eräs hyperbolinen paraboloidi Se on pinta, jonka yleinen yhtälö Cartesian koordinaateissa (x, y, z) kohtaa seuraavan yhtälön:

(for)² - (ja/b)² - Z = 0.

"Paraboloidi" -kirkko tulee siitä, että muuttuja z riippuu X- ja Y -muuttujien neliöistä. Vaikka adjektiivi "hyperbolinen" johtuu siitä, että hyperbolan yhtälöllä on kiinteät arvot z. Tämän pinnan muoto on samanlainen kuin hevosen ratsastustuolissa.

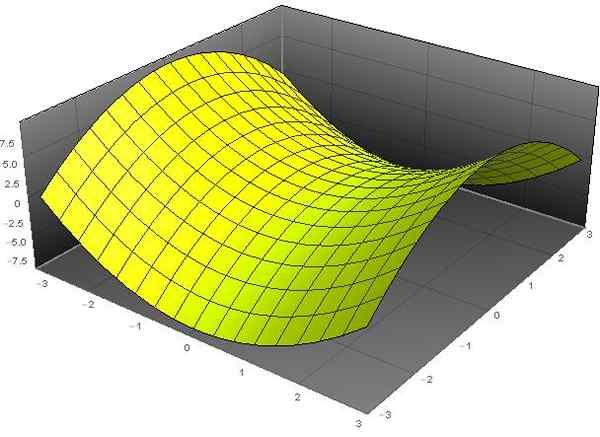
Kuvio 1. Hyperbolinen paraboloidi Z = x² - ja². Lähde: f. Zapata kautta Wolfram Mathematica.

[TOC]

Hyperbolisen paraboloidin kuvaus

Ymmärtääksesi hyperbolisen paraboloidin luonteen, seuraava analyysi tehdään:

1.- Erityinen tapaus otetaan A = 1, B = 1, toisin sanoen, että paraboloidin Cartesian yhtälö pysyy nimellä Z = x² - ja².

2.- Niitä pidetään ZX -tasossa rinnakkaisina, eli y = cttte.

3.- Y = ctte on z = x² - C, joka edustaa vertauksia oksat ylös ja kärjessä XY -tason alapuolella.

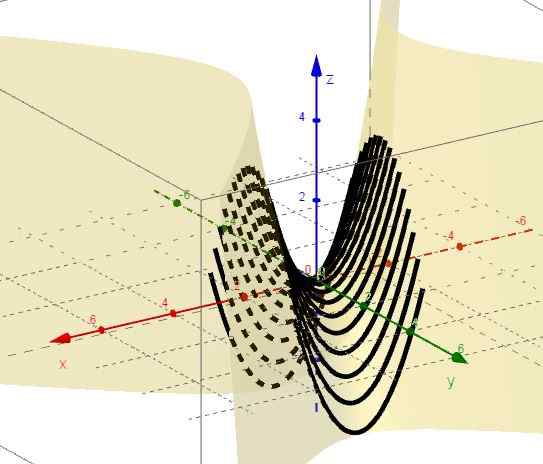Kuva 2. Käyrien perhe z = x² - C. Lähde: f. Zapata Geogebran kautta.

4.- X = ctte on z = c - y², joka edustaa vertauksia oksat alas ja kärkipiste XY -tason yläpuolella.

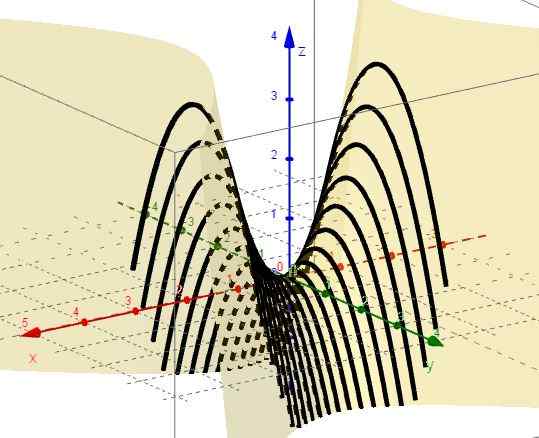Kuva 3. Käyrien perhe z = c - ja². Lähde: f. Zapata Geogebran kautta.

5.- Z = ctte on c = x² - ja², jotka edustavat hyperboloja XY -tason suuntaisesti tasoilla. Kun c = 0 on kaksi viivaa (A +45º ja -45º X -akselille), jotka sieppataan XY -tason alkuperästä.

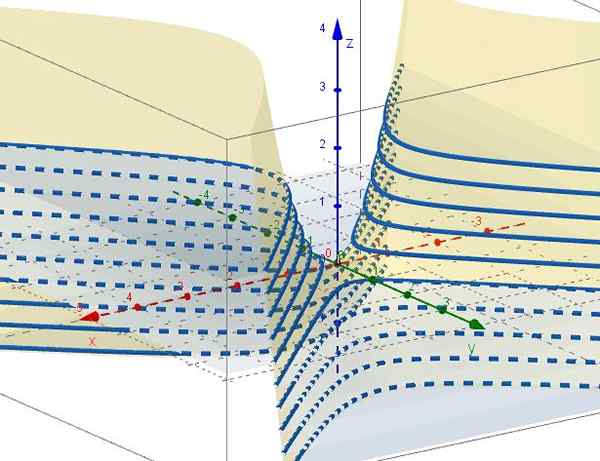Kuva 4. Käyrien perhe x² - ja² = C. Lähde: f. Zapata Geogebran kautta ..

Hyperbolisen paraboloidin ominaisuudet

1.- Neljä eri pistettä kolmen dimensionaalisessa tilassa määrittelevät yhden ja vain hyperbolisen paraboloidin.

Se voi palvella sinua: Rajoita ominaisuuksia (esimerkkien kanssa)

2.- Hyperbolinen paraboloidi on a kaksinkertaisesti säännelty pinta. Tämä tarkoittaa, että huolimatta kaarevasta pinnasta, hyperbolisen paraboloidin jokaiselle pisteelle kaksi eri viivaa kulkee kokonaan hyperboliseen paraboloidiin. Toinen pinta, joka ei ole taso ja on kaksinkertaisesti säännelty Vallankumous hyperboloidi.

Juuri hyperbolisen paraboloidin toinen ominaisuus on mahdollistanut sen laajan käytön arkkitehtuurissa, koska pinta voidaan tuottaa palkeista tai suorista jousista.

Hyperbolisen paraboloidin toinen ominaisuus mahdollistaa sen vaihtoehtoisen määritelmän: Se on pinta, joka voidaan luoda suoralla liikkuvalla viivalla, joka on yhdensuuntainen kiinteän tason kanssa ja leikkaa kaksi kiinteää viivaa, jotka toimivat oppaana. Seuraava kuva selventää tätä hyperbolisen paraboloidin vaihtoehtoista määritelmää:

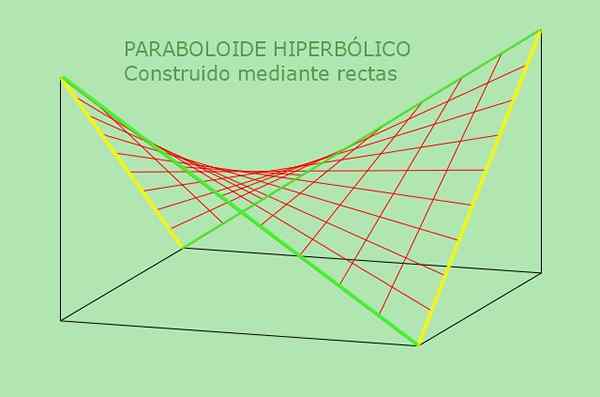Kuva 5. Hyperbolinen paraboloidi on kaksinkertaisesti säännelty pinta. Lähde: f. Zapata.

Ratkaistu esimerkki

- Esimerkki 1

Osoita, että yhtälö: Z = xy, vastaa hyperbolista paraboloidia.

Ratkaisu

Muutos sovelletaan X- ja Y -muuttujissa, jotka vastaavat Cartesian -akselien pyörimistä +45 -akselin Z: n suhteen. Vanhat X- ja Y -koordinaatit muutetaan uuteen x 'e: ksi ja' seuraavien suhteiden mukaan:

x = x ' - y'

y = x ' + ja'

Vaikka Z -koordinaatti pysyy samana, se on z = z '.

Korvaamalla yhtälössä Z = x ja meillä on:

z '= (x' - y ') (x' + y ')

Kun soveltaa eron merkittävää tuotetta summan mukaan, se on neliöeron, se on:

Z '= x'² - ja'²

joka vastaa selvästi hyperbolisen paraboloidin määritelmää.

XY -akselin yhdensuuntaisten tasojen sieppaaminen hyperbolisen paraboloidi z = x: n kanssa ja määrittävät tasapainon hyperbolat, joilla on asymptootteja tasot x = 0 e y = 0.

Voi palvella sinua: Miletus sellainen lause

- Esimerkki 2

Määritä parametrit -lla ja b - hyperbolisesta paraboloidista, joka kulkee pisteiden A (0, 0, 0) läpi; B (1, 1, 5/9); C (-2, 1, 32/9) ja D (2, -1, 32/9).

Ratkaisu

Ominaisuuksiensa mukaan neljä pistettä kolmen dimensionaalisessa tilassa määrittää yhden hyperbolisen paraboloidin. Yleinen yhtälö on:

Z = (x/a)² - (ja/b)²

Korvaamme annetut arvot:

Pisteelle A sinulla on 0 = (0/A)² - (0/B)², Yhtälö, joka täyttyy riippumatta parametrien A ja B arvoista.

Vaihtopiste B saadaan:

5/9 = 1/a² - 1 b²

Kun taas pisteelle C on edelleen:

32/9 = 4/a² - 1 b²

Lopuksi pisteelle D saadaan:

32/9 = 4/a² - 1 b²

Joka on identtinen edellisen yhtälön kanssa. Lyhyesti sanottuna yhtälöjärjestelmä tulisi ratkaista:

5/9 = 1/a² - 1 b²

32/9 = 4/a² - 1 b²

Ensimmäisen yhtälön vähentäminen saadaan:

27/9 = 3/a² mikä tarkoittaa sitä² = 1.

Samoin ensimmäisen yhtälön ensimmäisen yhtälö vähennetään, saadaan:

(32-20)/9 = 4/A² - 4/a² -1 b² + 4/b²

Sitä yksinkertaistetaan seuraavasti:

12/9 = 3/b² ⇒ B² = 9/4.

Lyhyesti sanottuna hyperbolisella paraboloidilla, joka kulkee pisteiden A, B, C ja D läpi, on Cartesian yhtälö, jonka on antanut:

Z = x² - (4/9) ja²

- Esimerkki 3

Hyperbolisen paraboloidin ominaisuuksien mukaan kaksi linjaa, jotka ovat täysin mukana, kulkevat jokaiselle pisteelle. Tapauksessa Z = x^2 - y^2 etsi kahden viivan yhtälö, jotka kulkevat pisteen P (0, 1, -1), jotka kuuluvat selvästi hyperboliseen paraboloidiin, siten, että kaikki näiden linjojen kohdat kuuluvat myös sama.

Ratkaisu

Käyttämällä neliöiden eron merkittävää tuotetta, hyperbolisen paraboloidin yhtälö voidaan kirjoittaa seuraavasti:

Voi palvella sinua: nelikulmainen: elementit, ominaisuudet, luokittelu, esimerkit

(x + y) (x - y) = c z (1/c)

Missä c on nollavakio.

Yhtälö x + y = c z ja yhtälö x - y = 1/c vastaa kahta tasoa, joissa on normaali vektori n= y m=. Vektorituote m x n = Kahden tason linjan risteyksen suunta antaa meille. Sitten yhdellä viivoista, jotka kulkevat pisteen P läpi ja kuuluu hyperboliseen paraboloidiin, on parametrinen yhtälö:

= + t

C: n määrittämiseksi korvaamme pisteen P yhtälössä x + y = c z, saadaan:

C = -1

Samoin, mutta ottaen huomioon yhtälöt (x - y = k z) ja (x + y = 1/k) Sinulla on viivan parametrinen yhtälö:

= + s k = 1.

Lyhyesti sanottuna, kaksi riviä:

= + t y = + s

Ne ovat kokonaan sisältäneet hyperbolisen paraboloidin Z = x² - ja² Pisteen läpi (0, 1, -1).

Tarkistuksena oletetaan, että t = 1 mikä antaa meille pisteen (1,2, -3) ensimmäisellä rivillä. Sinun on tarkistettava, onko se myös paraboloidilla z = x² - ja²-

-3 = 1² - 2² = 1 - 4 = -3

Joka vahvistaa, että käytännössä se kuuluu hyperbolisen paraboloidin pintaan.

Arkkitehtuurin hyperbolinen paraboloidi

Kuva 6. Valencian valtameri (Espanja).Lähde: Wikimedia Commons.

Suuret avantgarde-arkkitehdit ovat käyttäneet hyperbolista paraboloidia arkkitehtuurissa, joista espanjalaisen arkkitehdin Antoni Gaudín (1852-1926) nimet ja erityisesti espanjalaiset Félix Candela (1910-1997) ovat erityisen erityisesti.

Alla on joitain teoksia, jotka perustuvat hyperboliseen paraboloidiin:

-Arkkitehti Félix Candela Cuernavacan kaupungin (Meksiko) kappeli.

-Valencian valtameri (Espanja), myös Félix Candela.

Viitteet

1. Matematiikan tietosanakirja. Hallitsematon pinta. Palautettu: Encyclopediaofmath.org
2. Llera rubén. Hyperbolinen paraboloidi. Palautettu: Rubenllera.WordPress.com
3. Weisstein, Eric W. ”Hyperbolinen paraboloidi.”Mathworld-a Wolfram -verkkoresurssi. Toipunut: MathWorld.Susi.com
4. Wikipedia. Paraboloidi. Haettu: vuonna.Wikipedia.com
5. Wikipedia. Paraboloidi. Palautettu: on.Wikipedia.com
6. Wikipedia. Hallitsematon pinta. Haettu: vuonna.Wikipedia.com