Aritmeettisen esittelyn, sovellusten, harjoitusten peruslause

Hän Aritmeettisen peruslause Hän toteaa, että mikä tahansa suurempi kuin 1 luonnollinen lukumäärä voidaan jakaa alareunan lukumäärän - pitämisen - ja tämä muoto on ainutlaatuinen kyseiselle lukulle, vaikka tekijöiden järjestys voi olla erilainen.

Muista, että pääluku p Se myöntää vain positiivisina jakautuneina ja 1. Seuraavat numerot ovat serkkuja: 2, 3, 5, 7, 11, 13 ja niin edelleen, koska siellä on ääretöntä. Numeroa 1 ei pidetä serkkua yhdellä jakajalla.

Kuvio 1. Euclides (vasen) osoitti aritmeettisen peruslauseen kirjaelementeissä (350 a.C.), Ja ensimmäinen täydellinen esittely johtuu Carl F: stä. Gauss (1777-1855) (oikealla). Lähde: Wikimedia Commons.

Heidän puolestaan ​​kutsutaan numeroita, jotka eivät täytä edellä mainittua koostetut numerot, AS 4, 6, 8, 9, 10, 12, 14 ... Otetaan esimerkiksi numero 10 ja näemme heti, että se voidaan hajottaa 2 ja 5 -tuotteena:

10 = 2 × 5

Sekä 2 että 5 ovat todellakin alkulukuja. Lause toteaa, että tämä on mahdollista mille tahansa numerolle n:

Missä p₁, p₂, p₃… P_{r -} Ne ovat ensisijaisia ​​numeroita ja k₁, k -k -₂, k -k -₃,... k_{r -} Ne ovat luonnollisia lukuja. Niin, että alusluvut toimivat kuin tiilet, joista kerroksella luonnolliset numerot on rakennettu.

[TOC]

Aritmeettisen peruslauseen osoittaminen

Se alkaa osoittaa, että jokainen luku voi hajota ensisijaisissa tekijöissä. Olla luonnollinen luku N> 1, serkku tai yhdiste.

Esimerkiksi jos n = 2, se voidaan ilmaista seuraavasti: 2 = 1 × 2, joka on serkku. Samoin jatkamme seuraavia numeroita:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Jatkamme näin, hajottaen kaikki luonnolliset numerot, kunnes saavutamme numeron n -1. Katsotaanpa, voimmeko tehdä sen seuraavalla numerolla: n.

Jos n on serkku, voimme hajottaa sen nimellä n = 1 × N, mutta oletetaan, että n on koostettu ja siinä on jakaja D, loogisesti vähemmän kuin n:

Voi palvella sinua: Kuvailevat tilastot: historia, ominaisuudet, esimerkit, käsitteet

1< d < n.

Kyllä n/d = p₁, P -kanssa₁ Päämäärä, sitten n kirjoitetaan seuraavasti:

n = p₁.d -d

Jos d on serkku, ei ole muuta tekemistä, mutta jos ei ole, on numero n₂ joka on D: n jakaja ja vähemmän kuin tämä: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Toiselle serkkulle P₂-

d = p₂ n₂

Että korvaamalla alkuperäisessä numerossa n antaisi:

n = p₁ .p₂ .n₂

Oletetaan nyt n₂ Se ei myöskään ole alkuluku ja kirjoitamme sen alkuluku P -tuotteena₃, hänen jakautuneelle₃, sellainen, että n₃ < n₂ < n₁ < n:

n₂ = p₃.n₃ → n = p₁ p₂ p₃.n₃

 Toistamme tämän toimenpiteen rajallisen määrän kertoja, kunnes saat:

n = p₁.p₂.p₃ … P_{r -}

Tämä tarkoittaa, että on mahdollista hajottaa kaikki kokonaisluvut 2: sta numeroon N, päälukujen tuotteena.

Hajoamisen ainutlaatuisuus päätekijöissä

Varmistetaan nyt, että lukuun ottamatta tekijöiden järjestystä, tämä hajoaminen on ainutlaatuinen. Oletetaan, että voit kirjoittaa kahdella tavalla:

n = p₁.p₂.p₃ … P_{r -} = q_1.Q -₂.Q -₃… Q_s  (R ≤ s)

Tietysti q₁, Q -₂, Q -₃… Ne ovat myös päälukuja. P -nimellä₁ Jaa (Q_1.Q -₂.Q -₃… Q_s) Sitten p₁ Se on yhtä suuri kuin mikä tahansa "Q", ei väliä Mikä niin voimme sanoa, että p₁ = q₁. Jaamme n p: n välillä₁ Ja saamme:

p₂.p₃ … P_{r -} =_.Q -₂.Q -₃… Q_s

Toistamme menettelyn jakaa kaiken p: n välillä_{r -}, Sitten saamme:

1 = Q_R+1… Q_s

Mutta q: lle ei ole mahdollista päästä_R+1… Q_s = 1 Kun r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Sovellukset

Kuten olemme aiemmin sanoneet, ensisijaiset numerot edustavat jos haluat, numeron atomit, niiden peruskomponentit. Joten aritmeettisen peruslauseen on lukuisia sovelluksia, ilmeisin: voimme työskennellä helpommin suurilla numeroilla, jos ilmaisemme niitä pienempien lukujen tuotteena.

Voi palvella sinua: kokonaiset numerot

Samoin voimme löytää maksimaalisen yleisen moninkertaisen (M.c.m.) ja suurin yhteinen jakaja (m.C.D -d.;.

Lisäksi ensisijaiset luvut ovat erittäin arvoituksellisia. Niissä ei vielä tunnisteta mallia, eikä ole mahdollista tietää, mikä seuraava on. Suurin tietokoneet löysivät aikoja, ja se on 24.862.048 numerot, Vaikka uudet prime -numerot ilmestyvät harvemmin joka kerta.

Primon numerot luonteeltaan

Yhdysvaltojen koillisessa asuvat sykli- tai chicharras -sikadat ilmenevät 13 tai 17 vuoden jaksoissa. Molemmat ovat päälukuja.

Tällä tavoin Chicharras välttää samaan aikaan saalistajien tai kilpailijoiden kanssa, joilla on muita syntymäaikaa, eikä erilaiset chicharra -lajikkeet kilpailevat keskenään, koska ne eivät ole samanaikaisesti samana vuonna.

Kuva 2. Yhdysvaltojen taikuus Cicada del Este syntyy 13 tai 17 vuoden välein. Lähde: PxFuel.

Primo -numerot ja online -ostot

PRIMO -numeroita käytetään kryptografiassa pitämään luottokorttien yksityiskohdat, kun ostat online -ostoksia. Tällä tavoin tiedot, jotka ostaja saapuu tarkasti kauppaan, eksymättä tai putoaa häikäilemättömiin ihmisiin.

Kuten? Korttitiedot koodataan numeroon n, joka voidaan ilmaista alkulukuina. Nämä ensisijaiset numerot ovat avain, joka paljastaa tiedot, mutta ne ovat yleisölle tuntemattomia, ne voidaan dekoodata vain siinä verkossa, johon ne ohjataan.

Lukumäärän hajottaminen tekijöiksi on helppo tehtävä, jos numerot ovat pieniä (nähdessään harjoitukset ratkaistu), mutta tässä tapauksessa niitä käytetään 100 numeron tärkeinä alusmäärinä, jotka kertomalla ne antavat paljon suurempia numeroita, joiden yksityiskohtainen hajoaminen merkitsee valtava työ.

Voi palvella sinua: Täsmällinen arvio

Ratkaisut

- Harjoitus 1

Hajota 1029 ensisijaisiksi tekijöiksi.

Ratkaisu

1029 on jaettavissa 3: lla. Se tunnetaan, koska lisäämällä numeroita summa on 3: 1+0+2+9 = 12. Koska tekijöiden järjestys ei muuta tuotetta, voimme aloittaa sieltä:

1029 3

343

1029 = 3 × 343

Toisaalta 343 = 7³, niin:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Ja koska sekä 3 että 7 ovat ensisijaisia ​​lukuja, tämä on hajoaminen 1029.

- Harjoitus 2

Tekijä Trinomial X² + 42x + 432.

Ratkaisu

Trinomiaalinen kirjoitetaan uudelleen muodossa (x+a). (x+b) ja meidän on löydettävä A: n ja B: n arvot, niin että:

A+B = 42; -lla.B = 432

Numero 432 hajoaa ensisijaisiksi tekijöiksi ja sieltä sen valitsee Tanteo, asianmukainen yhdistelmä 42: een lisättyihin tosiasioihin.

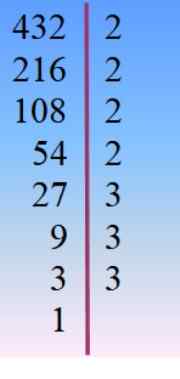
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Sieltä on useita mahdollisuuksia kirjoittaa 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

Ja kaikki voidaan löytää yhdistämällä tuotteet päätekijöiden välillä, mutta ehdotetun harjoituksen ratkaisemiseksi ainoa riittävä yhdistelmä on: 432 = 24 × 18, koska 24 + 18 = 42, sitten:

x² + 42x + 432 = (x + 24). (x +18)

Viitteet

1. Baldor, a. 1986. Käytännöllinen teoreettinen aritmeettinen. Amerikkalaisten tekstien toimittaja kulttuuriyhtiö S.-Lla.
2. BBC -maailma. Luonnon piilotettu koodi. Haettu osoitteesta: BBC.com.
3. Leonista, Manuel.Primon numerot: Internet -huoltajat. Palautettu: blogit.20 minuuttia.On.
4. Yksinäinen. Numeroteoria I: Aritmeettisen peruslause. Haettu: Theoriadenumeros.Wikidot.com.
5. Wikipedia. Aritmeettisen peruslause. Palautettu: on.Wikipedia.org.