Suuntaissärmiö

Rinnakkaiskipit ovat kuusi -puolustavia geometrisia lukuja, joissa vastakohdat ovat yhdensuuntaisia ​​toistensa kanssa. Esimerkki: tiili, kenkälaatikko, kauha jne.

Mikä on rinnakkain?

Eräs suuntaissärmiö Se on kuuden kasvot muodostama geometrinen runko, jonka pääpiirteet ovat, että kaikki sen kasvot ovat rinnakkaisia ​​ja myös sen vastakkaisia ​​kasvoja ovat yhdensuuntaiset toistensa kanssa. Se on yleinen polyhedroni jokapäiväisessä elämässämme, koska löydämme sen kenkälaatikoista, tiilin muodosta, mikroaaltouunin muodoista jne.

Polyedronina ollessa rinnakkaispiped sisältää äärellisen tilavuuden ja kaikki sen kasvot ovat tasaisia. Se on osa prismaryhmää, jotka ovat polyhedraa, jossa kaikki sen kärjet sisältyvät kahteen rinnakkaiseen tasoon.

Rinnakkaiskipitetyn elementit

Kasvot

Ne ovat jokainen alueelle, jotka muodostuvat rinnakkaisohjelmien avulla, jotka rajoittavat rinnakkaiskipiä. Rinnakkaiskipillä on kuusi kasvoja, joissa jokaisella kasvolla on neljä vierekkäistä kasvot ja päinvastoin. Lisäksi jokainen kasvo on yhdensuuntainen sen vastakkaisen kanssa.

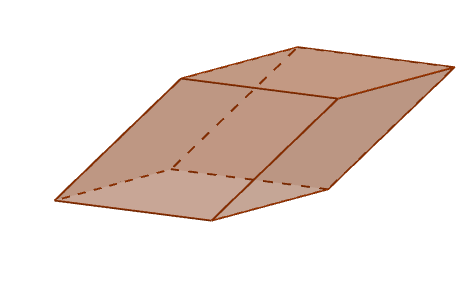Rinnakkaispiped -näkökulma

Reunat

Ne ovat kahden pinnan yleinen puoli. Yhteensä rinnakkaiskipillä on kaksitoista reunaa.

Kärki

Kolmen pinnan yleinen kohta on vierekkäinen kahdesta kahteen. Rinnakkaiskipillä on kahdeksan kärkeä.

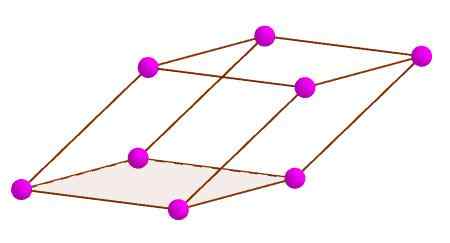Rinnakkaiskipiä

Diagonaali

Kun otetaan huomioon kaksi rinnakkaiskipiä vastapäätä toisiaan, voimme piirtää linjasegmentin, joka kulkee toisen pinnan kärkipisteestä toisen vastakkaiseen kärkeen.

Tätä segmenttiä kutsutaan rinnakkaiskipitetyksi diagonaaliksi. Jokaisessa rinnakkaiskipillä on neljä diagonaalia.

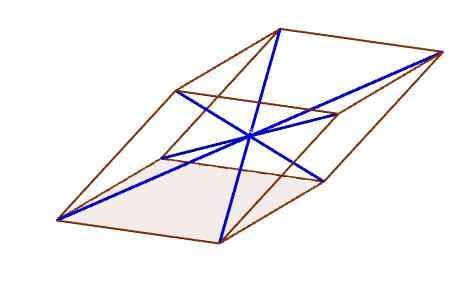Rinnakkaiskipillinen diagonaalit

Keskusta

Se on kohta, jossa kaikki diagonaalit leikkaavat.

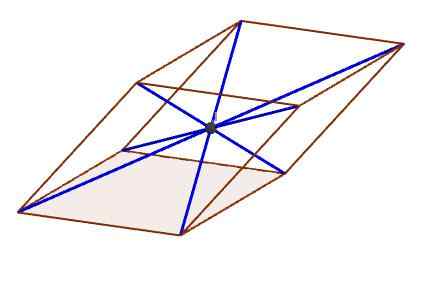Kuvan kohta osoittaa keskuksen, jossa kaikki diagonaalit leikkaavat

Rinnakkaiskipitetyn ominaisuudet

Kuten jo mainitsimme, tällä geometrisella rungolla on kaksitoista reunaa, kuusi kasvot ja kahdeksan kärkeä.

Rinnakkaiskipiteissä voidaan tunnistaa kolme neljästä reunasta muodostettua sarjaa, jotka ovat yhdensuuntaisia ​​toistensa kanssa. Lisäksi näiden sarjojen reunat noudattavat myös saman pituisia ominaisuuksia.

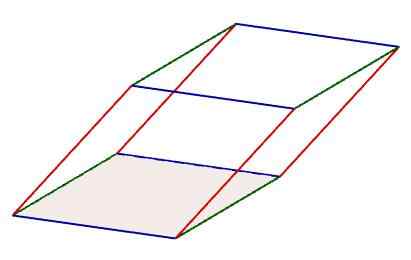Rinnakkaiskipitetyn ominaisuudet

Toinen omaisuus poseeraa.

Lisäksi rinnakkaiskipit, jotka ovat kupera polyhedros, noudattavat Eulerin polyhedros -lausetta, mikä antaa meille suhteen kasvojen lukumäärän, reunojen lukumäärän ja kärjen lukumäärän välillä. Tämä suhde on annettu seuraavan yhtälön muodossa:

C + V = A + 2

Tämä ominaisuus tunnetaan Eulerin ominaispiirteinä. Missä c on kasvojen lukumäärä, kärkipisteiden lukumäärä ja reunojen lukumäärä.

Tyypit paralleepípedos

Voimme luokitella Parallepípedon heidän kasvojensa perusteella seuraaviin tyyppeihin:

Ortoedro

Ne ovat Parallepípedos, jossa heidän kasvonsa koostuvat kuudesta suorakulmusta. Jokainen suorakulmio on kohtisuorassa niiden kanssa, joiden kanssa se jakaa reunaa. Ne ovat yleisimpiä jokapäiväisessä elämässämme, tämä on tavanomainen kenkä- ja tiililaatikoiden muoto.

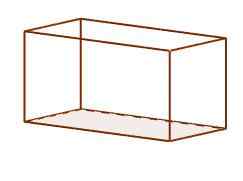Ortoedro

Tavallinen kuutio tai heksaedro

Tämä on erityinen tapaus edellisestä, jossa kukin kasvot ovat neliö.

Voi palvella sinua: ellipsiTavallinen kuutio tai heksaedro

Kuutio on myös osa geometrisiä kappaleita, joita kutsutaan platooniseksi kiinteiksi aineiksi. Platoninen kiinteä aine on kupera polyhedronia, joten sekä sen kasvot että sen sisäkulmat ovat yhtä suuret kuin toiset.

Romboedro

Se on rinnakkaispiped, jossa on rhombus. Nämä rhombukset ovat kaikki yhtä suuret kuin toiset, koska ne jakavat reunoja.

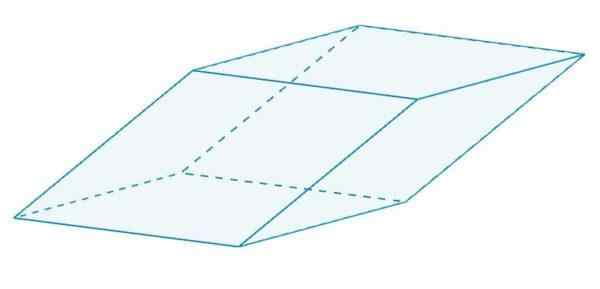Romboedro

Romboiedro

Hänen kuusi kasvonsa ovat rhboidia. Muista, että rhomboid. Rhomboidit ovat rinnakkaisia ​​ohjelmia, jotka eivät ole neliömäisiä, suorakulmioita, eikä rhombuksia.

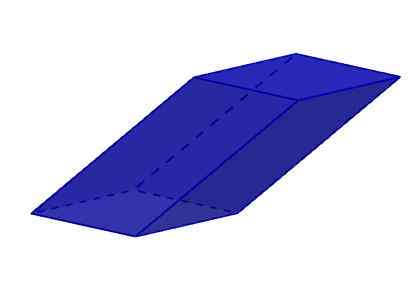Romboiedro

Toisaalta vinot rinnakkaiskipit ovat niitä, joissa ainakin yksi korkeus ei vastaa sen reunaa. Tässä luokituksessa voimme sisällyttää rhomboedrot ja rhomboiedros.

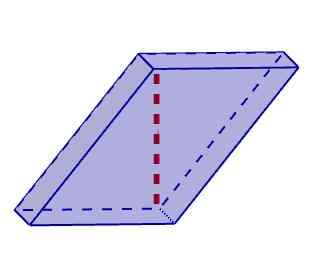Vinossa rinnakkaiskipillinen

Diagonaalinen laskenta

Ortoedron diagonaalin laskemiseksi voimme käyttää pythagoras -lausetta r³.

Muista, että ortoedrolla on ominaisuus, että molemmat osapuolet ovat kohtisuorassa sivujen kanssa, joilla on reuna. Tästä tosiasiasta voimme päätellä, että jokainen reuna on kohtisuorassa niiden kanssa, jotka jakavat Vertexin.

Ortoedron diagonaalin pituuden laskemiseksi jatkamme seuraavasti:

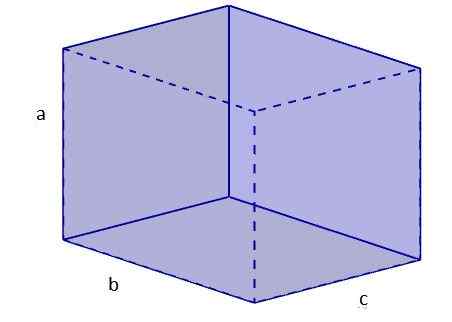
1. Laskemme yhden kasvojen diagonaalin, jonka perustamme pohja. Tätä varten käytämme Pythagoras -lausetta. Nimetään se diagonaali d_{b -}.

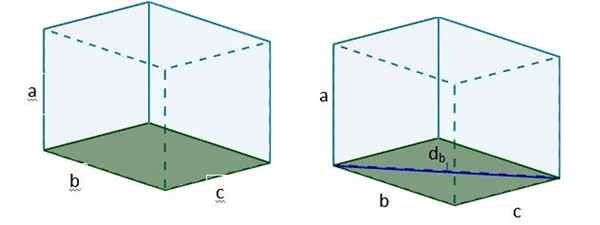
2. Sitten D: llä_{b -} Voimme muodostaa uuden suorakulmion kolmion siten, että mainitun kolmion hypotenuse on diagonaalinen D -haku.

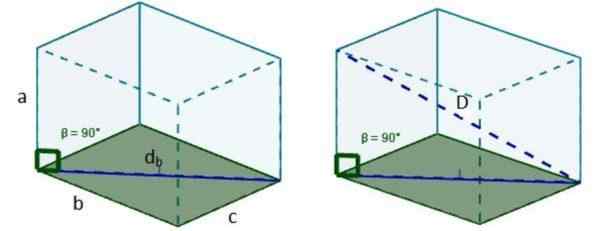
3. Käytämme uudelleen Pythagoras -lausetta ja meillä on, että kyseisen diagonaalin pituus on:

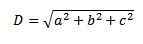
Toinen tapa laskea diagonaali graafisemmalla tavalla on vapaiden vektorien summa.

Muista, että kaksi vapaata vektoria A ja B lisätään asettamalla vektorin B häntä vektorin kärjessä A.

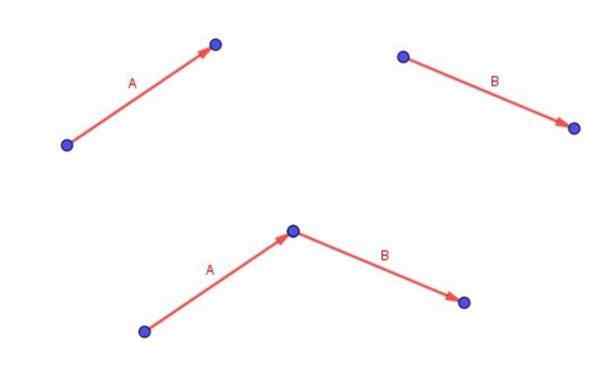
Vektori (A + B) on se, joka alkaa A: n hännästä ja päättyy B: n kärjessä.

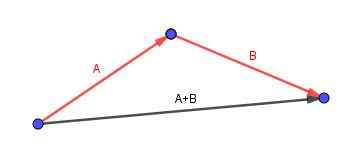
Harkitse rinnakkaiskipiä, johon haluamme laskea diagonaalin. Tunnistamme reunat kätevillä suuntautuneilla vektoreilla.

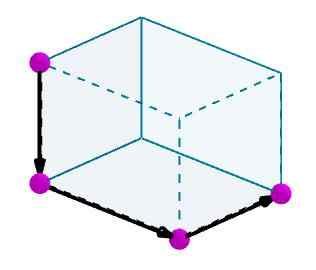
Sitten lisäämme nämä vektorit ja tuloksena oleva vektori on rinnakkaiskipien diagonaali.

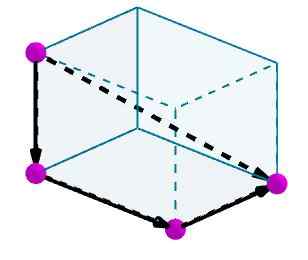
Rinnakkaiskipillinen alue

Rinnakkaiskipien pinta -ala annetaan kunkin sen kasvojen alueen summa.

Jos määritämme yhden sivun pohjana,

-Lla_Lens + Toinen_{B -} = Kokonaispinta -ala

Minne_Lens Se on yhtä suuri kuin kaikkien puolen vieressä olevien alueiden alue, jota kutsutaan sivualueeksi ja_{B -} Se on perusalue.

Riippuen rinnakkaiskipiteistä, joiden kanssa työskentelemme, voimme kirjoittaa mainitun kaavan uudelleen.

Ortoedron alue

Annetaan kaavalla

A = 2 (ab + bc + ca).

Esimerkki 1

Kun otetaan huomioon seuraava Orthoedro, sivuilla A = 6 cm, B = 8 cm ja C = 10 cm, laske rinnakkaiskipillinen alue ja sen diagonaalin pituus.

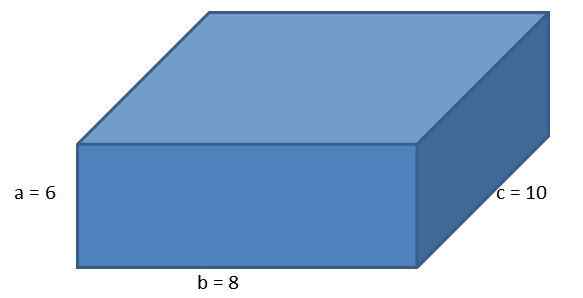
Käyttämällä kaavaa ortoedron alueelle

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Huomaa, että ortoedro on minkä tahansa sen neljän diagonaalin pituus.

Se voi palvella sinua: Määrittelemätön integraali: Ominaisuudet, sovellukset, laskenta (esimerkit)

Pythagoras -lauseen käyttäminen avaruuteen meidän on

D = (6² + 8² + 10²-A^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Kuutioalue

Koska jokaisella reunalla on sama pituus, meillä on a = b ja a = c. Korvaaminen edellisessä kaavassa

A = 2 (AA + AA + AA) = 2 (3a²) = 6a²

A = 6a²

Esimerkki 2

Pelikonsolin laatikko on kuution muoto. Jos haluamme kääriä tämän laatikon lahjapaperilla, kuinka paljon paperia vietämme tietäen, että kuution reunojen pituus on 45 cm?

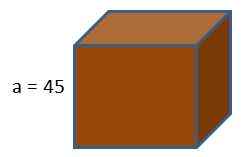
Käyttämällä kuutioalueen kaavaa saamme sen

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Rhomboedro

Koska kaikki sen kasvot ovat samat, se riittää laskemaan yhden alueen ja moninkertaistaa se kuusi.

Meillä on, että rhombuksen pinta -ala voidaan laskea sen diagonaalien avulla seuraavalla kaavalla

-Lla_{R -} = (Dd)/2

Tätä kaavaa käyttämällä seuraa, että rhomboedron kokonaispinta -ala on

-Lla_T = 6 (DD)/2 = 3DD.

Esimerkki 3

Seuraavan rhomboedron kasvot muodostuvat rhombus, jonka diagonaali ovat d = 7 cm ja d = 4 cm. Alueesi tulee olemaan

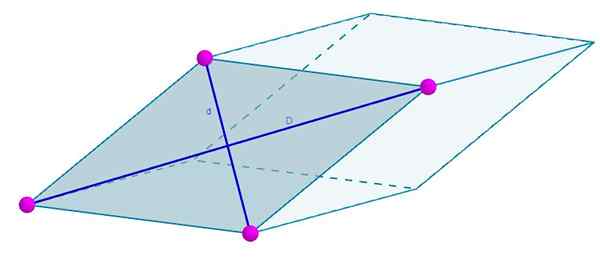
A = 3 (7 cm) (4 cm) = 84 cm².

Rhomboiedro

Rhomboedron pinta -alan laskemiseksi meidän on laskettava sen muodostavien rhboidien pinta -ala. Kun rinnakkaiskipit täyttävät kiinteistön, jolla vastakkaisilla puolilla on sama alue, voimme yhdistää sivut kolmeen ikäisensä.

Tällä tavalla meillä on, että alueesi tulee olemaan

-Lla_T = 2b₁h₁ + 2b₂h₂ + 2b₃h₃

Missä b_Yllyttää ovat sivut liittyvät sivuihin ja H_Yllyttää sen suhteellinen korkeus vastaa mainitut emäkset.

Esimerkki 4

Harkitse seuraavaa rinnakkaiskipiä,

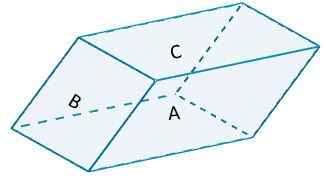
missä sivu A ja sivu A '(niiden vastakkainen puoli) perustuvat b = 10 ja korkeutta kohti h = 6. Merkittävällä alueella on arvo

-Lla₁ = 2 (10) (6) = 120

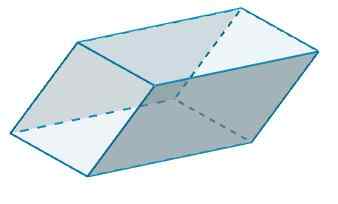
B ja b 'on b = 4 ja h = 6, sitten

-Lla₂ = 2 (4) (6) = 48

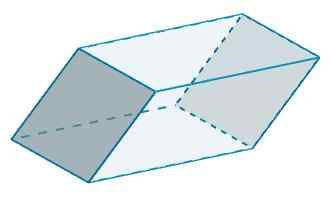
Ja c ja c 'ovat myös b = 10 ja h = 5,

-Lla₃ = 2 (10) (5) = 100

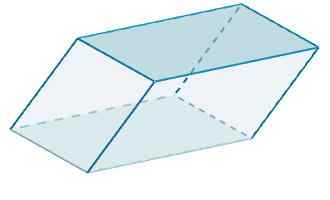
Lopuksi rhomboiedro -alue on

A = 120 + 48 + 100 = 268.

Rinnakkaiskipillinen tilavuus

Kaava, joka antaa meille rinnakkaiskipien tilavuuden, on yhden sen pinta -alan tuote mainitun kasvojen korkeuden vuoksi.

V = a_Ch_C

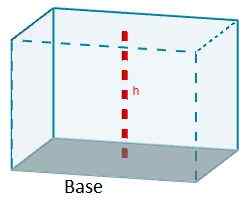
Rinnakkaiskipien tyypistä riippuen tätä kaavaa voidaan yksinkertaistaa.

Siten meillä on esimerkiksi, että ortoedron tilavuus annetaan

V = ABC.

Missä a, b ja c edustavat ortoedrojen reunojen pituutta.

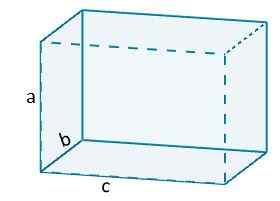
Ja kuutiotapauksessa on

V = a³

Esimerkki 1

Evästealaatikoihin on kolme erilaista mallia ja haluat.

Ensimmäinen on kuutio, jonka reunan pituus on A = 10 cm.

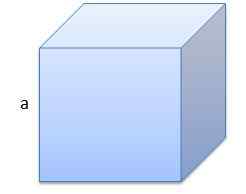
Sen tilavuus on v = 1000 cm³

Toinen on b = 17 cm, c = 5 cm, d = 9 cm.

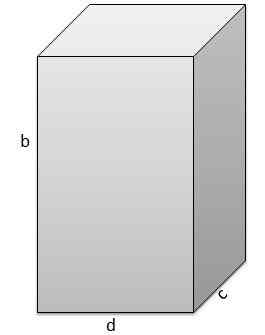
Ja siksi sen tilavuus on v = 765 cm³

Ja kolmannella on E = 9 cm, F = 9 cm ja g = 13 cm.

Ja sen tilavuus on v = 1053 cm³

Voi palvella sinua: kulmat, ominaisuudet ja esimerkit

Siksi laatikko, jolla on suurin tilavuus, on kolmas.

Toinen menetelmä rinnakkaiskipien tilavuuden saamiseksi on vektorialgebran turvaaminen. Erityisesti kolminkertainen skalaarituote.

Yksi kolminkertaisen skalaarisen tuotteen geometrisista tulkinnoista on rinnakkaiskipien tilavuus, jonka reunat ovat kolme vektoria, joilla on sama kärki kuin lähtökohta.

Tällä tavoin, jos meillä on rinnakkaispipejä ja haluamme tietää, mikä sen tilavuus on, se riittää edustamaan sitä koordinaattijärjestelmässä R: ssä³ samaan aikaan kuin yksi sen kärjistä alkuperän kanssa.

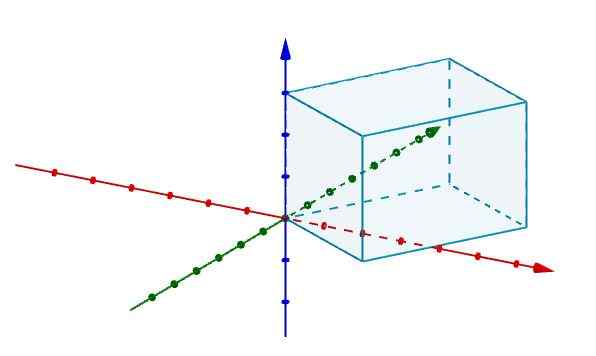
Sitten edustamme reunoja, jotka ovat yhtä mieltä alkuperästä vektoreilla, kuten kuvassa on esitetty.

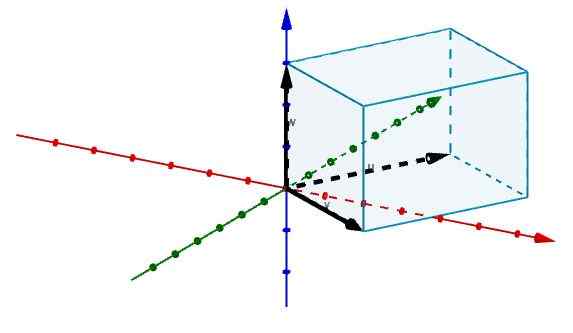
Ja tällä tavalla meillä on, että mainitun rinnakkaiskipien määrä on annettu

V = | AXB ∙ C |

Tai vastaava, tilavuus on 3 × 3 -matriisin määrittäjä, joka muodostuu reunavektorien komponenteista.

Esimerkki 2

Edustamalla seuraavaa rinnakkaiskipiä R: ssä³ Voimme nähdä, että sen määrittävät vektorit ovat seuraavat

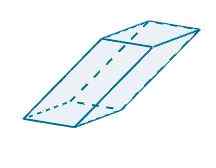
U = (-1, -3,0), V = (5, 0, 0) ja W = (-0.25, -4, 4)

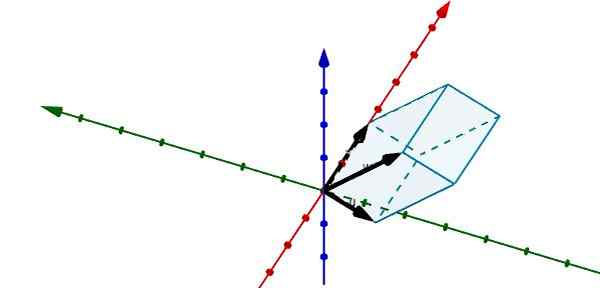
Käyttämällä kolminkertaista skalaarituotetta

V = | (UXV) ∙ W |

Uxv = (-1, -3,0) x (5, 0, 0) = (0,0, -15)

(UXV) ∙ W = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Tämä päättelee, että v = 60

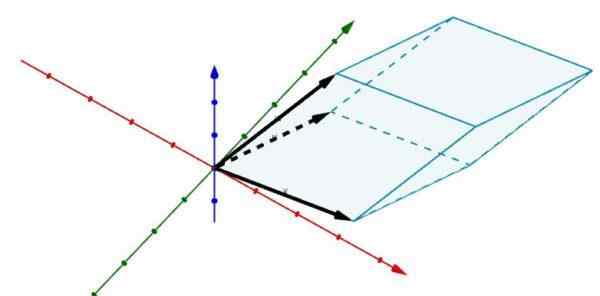
Harkitse nyt seuraavaa rinnakkaiskipiä R: ssä³ jonka reunat määräävät vektorit

A = (2, 5, 0), B = (6, 1, 0) ja C = (3, 4, 4)

Determinanttien käyttäminen antaa meille sen

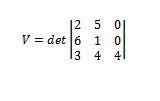
Siten meillä on, että mainitun rinnakkaiskipien tilavuus on 112.

Molemmat ovat vastaavia tapoja laskea tilavuus.

Täydellinen rinnakkainen

Se tunnetaan nimellä Euler -tiili (tai Euler -lohko) ortoedroon, joka täyttää ominaisuuden, että sen reunojen pituus ja kunkin kasvonsa pituus ovat kokonaisia ​​lukuja.

Vaikka Euler ei ollut ensimmäinen tutkija, joka tutki omaisuutta tapaavia ortoedereita, hän löysi heistä mielenkiintoisia tuloksia.

Pienin Euler-tiili löysi Paul Halcke (1662-1731) ja sen reunojen pituudet ovat A = 44, B = 117 ja C = 240.

Numeroteorian avoin ongelma on seuraava:

Onko olemassa täydellisiä ortoneja?

Tällä hetkellä tällä kysymyksellä ei vieläkään ole vastausta, koska ei ole ollut mahdollista todistaa, että ruumiita ei ole, mutta ketään ei ole löydetty.

Tähän mennessä on osoitettu, että täydellinen rinnakkaiskipillinen tekee. Ensimmäisen löydetyn reunojen pituudella arvot 103, 106 ja 271.

Viitteet

1. Kaveri, r. (1981). Ratkaisemattomat ongelmat lukuteoriassa. Jousto.
2. Landaverde, f. d -d. (1997). Geometria. Edistyminen.
3. Leithold, L. (1992). Laskelma analyyttisellä geometrialla. Harla, S.-Lla.
4. Rendon, a. (2004). Tekninen piirustus: Aktiviteettikirja 3 2. ylioppilastutkinto. Tebar.
5. Resnick, r., Halliday, D., & Krane, K. (2001). Vol fysiikka. 1. Meksiko: Mannermainen.