Odottaa viivakaavaa ja yhtälöitä, esitystä, esimerkkejä

Se vireillä oleva linja Kulman θ tangentti on, että tämä viiva muodostuu vaakasuoran akselin kanssa, joka valmistelukunnassa mitataan vastakkaiseen suuntaan kuin kellot. Minkä tahansa linjan kaltevuus on aina vakio, ja siksi se on yksi sen tärkeimmistä ominaisuuksista.

Sen laskemiseksi sinun on tiedettävä kaksi linjan pistettä, joiden koordinaatit ovat (x x₁,ja₁) ja (x₂,ja₂-A. Molempien pisteiden välillä piirretään segmentti, joka kuuluu linjaan ja sitten X: n välistä etäisyyttä edustavat segmentit vedetään₁ ja x₂, ja välillä ja välillä₁ ja ja₂, Kuten alemmassa kuvassa.

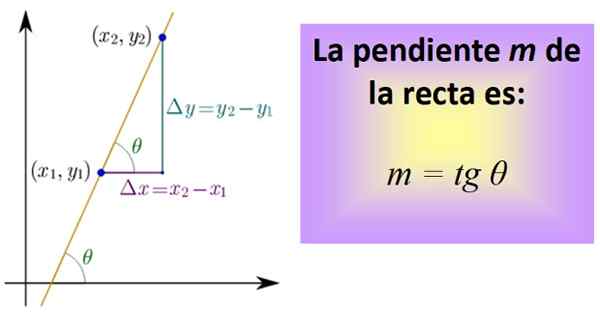
Kuvio 1. Linjan kaltevuus on kulman tangentti θ. Lähde: Wikimedia Commons.

Kolme segmenttiä muodostavat oikean kolmion, jonka jalat ovat: Δx = x₂ - x₁  ja ΔY = ja₂ - ja₁. Ne vastaavat vastaavasti vaakasuoraan siirtymään ja toiseen pystysuoraan.

Nyt määritetään osamäärä, nimeltään kulman tangentti ja lyhennetty tg θ, joka on juuri kaltevuus m linja:

m = tg θ = Δy / Δx

Huomaa, että linjalle tämä kulma pysyy vakiona, riippumatta sen tangentin laskemiseksi kohdistuvista pisteistä. Joka tapauksessa tämä arvo tarjoaa meille mittaan kuinka taipuvainen se on linja.

Valittujen pisteiden koordinaattien kautta kaltevuuskaava pysyy:

M = (y - y₁ ) / (X₂ - x₁-A

[TOC]

Graafinen esitys

Alla on useita tilanteita, joissa kaltevuus käsite on merkityksellinen. Sen arvo voidaan helposti laskea mittaamalla vastaava pystysuuntainen ja vaakasuuntainen siirtymä ja tekemällä sitten alussa ilmoitettu osoitus.

Tämä antaa meille kuvan jonkin rakenteen kaltevuudesta tai laskusta, kuten ramppi, katto tai tie:

Voi palvella sinua: Satunnainen näytteenotto: metodologia, edut, haitat, esimerkit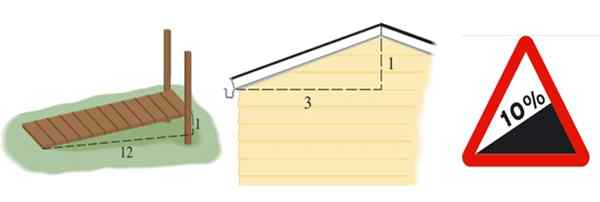 Kuva 2. Vasemmalta oikealle rampin, katto ja tien kaltevuus, jälkimmäinen ilmaisi prosentteina. Lähde: Stewart, J. Precáculculo ja Wikimedia Commons (oikea kuva).

Vasemmalla puolella 2 esitetyn rampin kaltevuus on M = 1/12, katto on M = 1/3 ja tie ilmaistaan ​​prosentteina. 10 %: n prosenttiosuus tarkoittaa, että jokaisesta vaakasuorasta etenevästä 100 metristä he ansaitsevat 10 metriä korkealle:

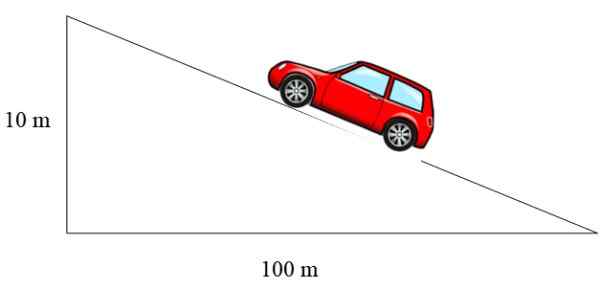Kuva 3. Ajoneuvo nousee kaltevuuden läpi, jonka kaltevuus on 10%. Lähde: f. Zapata.

Tässä tapauksessa kaltevuus on 10/100 = 0.1, joka ilmaistiin prosentteina, on 10%.

Kaltevuustyypit

Linjan kaltevuus voi olla positiivinen, negatiivinen tai tyhjä. Esimerkiksi kuviossa 1 esitetyllä viivalla on positiivinen kaltevuus. Arvostamme sitä heti, koska näemme, että linja on "nostettu", jos näemme sen vasemmalta oikealle.

Jos linja laskeutuu näkemään sen vasemmalta oikealle, sen kaltevuus on negatiivinen. Ja kun viiva on vaakasuora, sen kaltevuus on tyhjä.

Lopuksi pystysuorille viivoille kaltevuutta ei ole määritelty.

Kunkin tyypin graafinen esitys löytyy alla:

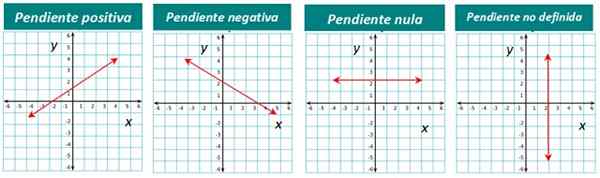Kuva 4. Linjat kaltevuutesi mukaan. Lähde: f. Zapata.

Kuinka kaltevuus lasketaan viiva?

Kaltevuuden laskeminen on hyvin yksinkertaista, sinun on vain löydettävä pystysuuntainen siirtymä ja vaakasuuntainen siirtymä ja tehtävä sitten kahden välillä näiden kahden välillä.

Kun sinulla on linjan piirtäminen Cartesian tasoon, nämä siirtymät valitsevat linjan P kaksi pistettä₁ Ja p₂, niiden koordinaattien määrittäminen ja alussa annetun määritelmän soveltaminen:

Voi palvella sinua: mikä edustaa kuusikulmion siirtymän pituutta

M = (y - y₁ ) / (X₂ - x₁ -A

Koska kaltevuuden arvo on riippumaton P: n valinnasta₁ Ja p₂ , Aiomme valita linjalle kuuluvan koordinaattien (x, y) pisteen P, jonka koordinaatit eivät tunne ja toinen kohta P₁ Kenen koordinaatit ovat: (x₁,ja₁-A.

Kaltevuus on:

M = (y - y₁) / (x - x₁-A

Voimme puhdistaa ja-

ja ja₁ = m (x - x₁-A

Oletetaan nyt, että p -₁ Se on linjan leikkaus pystysuoran akselin, koordinaattien (0, b) kanssa. Tämän korvaaminen edellisessä yhtälössä:

ja - b = m (x - 0) → y = mx + b

Tätä lauseketta kutsutaan muodossa olevan viivan yhtälöksi Odotettavissa - risteys, Koska viiva määritetään yksiselitteisesti, kun sen kaltevuus ja risteys pystysuuntaisen akselin kanssa tunnetaan.

Vain kaltevuuden tunteminen ei riitä karakterisoimaan linjaa tasolla, koska äärettömällä suoralla voi olla sama kaltevuus, mikä tarkoittaa, että ne ovat yhdensuuntaisia, mutta käyvät läpi muut kohdat.

Ratkaisut

- Harjoitus 1

Etsi seuraavassa kuvassa esitetyn viivan kaltevuus:

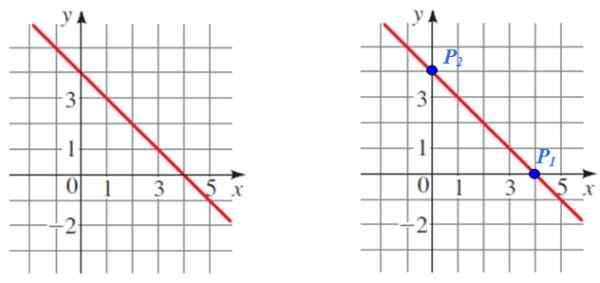Kuva 5. Linjan kaavion kautta valitaan sen kaltevuuden laskemiseksi. Lähde: f. Zapata.

Ratkaisu

P₁ Ja p₂ Ne ovat kahta helppoa -luettavaan pisteeseen, jotka palvelevat laskelmaa, toteavat myös, että ne ovat vastaavat risteykset koordinaattiakselien kanssa.

Kunkin pisteen koordinaatit ovat:

P₁ (4.0) ja P₂ (0,4)

Korvaamalla kaltevuusyhtälö:

M = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Kaltevuus on negatiivinen, jota odotettiin tarkkailun jälkeen grafiikkaa.

Voi palvella sinua: monimutkaiset numerot: Ominaisuudet, esimerkit, toiminnot

- Harjoitus 2

Etsi pisteen (1, -6) läpi kulkevan linjan yhtälö ja on yhdensuuntainen linjan Y = 2x - 3: n kanssa.

Ratkaisu

Etsityn viivan kaltevuuden on oltava sama kuin Y = 2x - 3, koska ne ovat yhdensuuntaisia. Tälle viivalle kaltevuus on M = 2, joten etsimällämme on muoto:

ja ja₁ = 2 (x - x₁-A

Nyt korvaamme pisteen, jonka kautta linjamme kulkee: x₁ = 1 ja₁ = -6.

ja - (-6) = 2 (x - 1)

Siksi y = 2x - 2 - 6 → y = 2x - 8

Esimerkit

Kaksi määrää voi liittyä siten, että kaavio on suora. Tällöin sanotaan, että määrillä on lineaarinen riippuvuus ja linjan kaltevuus voidaan tulkita syynä yhden muuttujan muutokseen toiseen.

Esimerkki 1

Oletetaan, että uima -allas on täynnä vettä a aste jatkuva. Luonnollisesti mitä enemmän aikaa kuluu, sitä enemmän vettä se varastoidaan. No, uima -altaan täytetty nopeus on tarkalleen linjan kaltevuus, joka liittyy tilavuuteen:

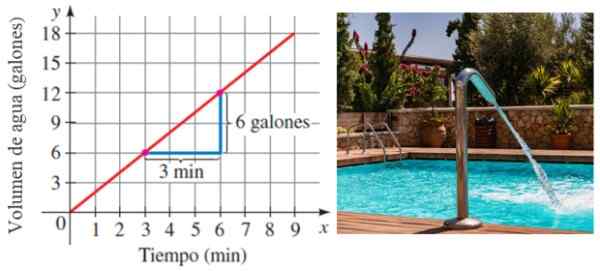Kuva 6. Kaltevuus muutoksen syynä. Lähde: Stewart, J./Pxfuel.

Tässä esimerkissä uima -allas täytetään nopeudella 6/3 gallonaa minuutissa tai 2 gallonaa/minuutti.

Esimerkki 2

Kun matkapuhelin liikkuu suorassa viivassa, jolla on vakio nopeus, asentokaavion kaltevuus riippuu ajasta, kukaan muu kuin mainittu nopeus. Kaavio näyttää liikkuvan, jolla on positiivinen nopeus, mikä tarkoittaa, että se on siirtymässä pois alkuperästä.

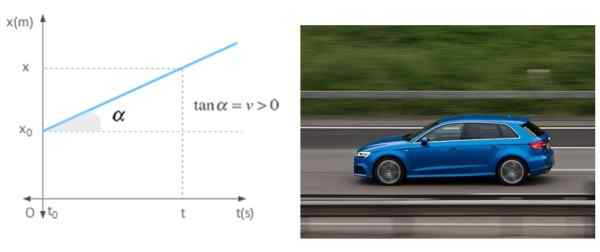Kuva 7. Versus -aikakaavion kaltevuus on liikkuvan nopeus yhtenäisessä suorakulmiossa. Lähde: Wikimedia Commons/Pixabay.

Viitteet

1. Alvarez, J. Tien kaltevuus. Toipunut: Geogebra.On.
2. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
3. Hoffman, J. Matematiikan aiheiden valinta. Osa 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
6. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.