Väestö ja otos

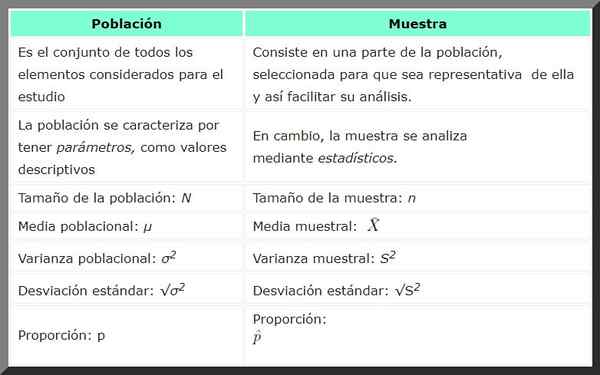
Se Erot populaation ja näytteen välillä Tilastoissa ne johtuvat siitä, että väestö on tutkittava elementtien maailmankaikkeus, kun taas otos on edustava osa väestöä.

Analysoi sarjasta otetun näytteen kokonaisuuden sijasta. Katsotaan alla yksityiskohtaisemmin tärkeimmät erot molempien käsitteiden välillä.

Nyt on selvää, että populaatio voi koostua erittäin suuresta elementtien joukosta: ihmisistä, eläimistä, mikro -organismeista tai hiukkasista. Kunkin näiden elementtien tutkimuksen käsitteleminen kuluttaa erikseen paljon resursseja, aikaa ja vaivaa.

Mutta valittaessa huolellisesti valittua näytettä, heidän tutkimuksestaan ​​johdetut tulokset ulottuvat populaatioon ilman merkittäviä tietotappioita.

	Väestö	Näyte
Määritelmä	Kaikkien tutkimuksen otettujen elementtien joukko.	Se on osa väestöä, joka on valittu edustavaksi ja helpottaa sen analyysiä.
Symboli	Väestökoko: n	Näytteen koko: n
Analyysi	On parametreja, kuvaavat arvot.	Sitä analysoidaan tilastoilla.
Esimerkit	Metsässä asuvien lintujen kokonaismäärä.	Tutkimusta varten 1000 lintua otetaan metsästä.

Mikä on väestö?

Väestö on paikan asuttavien ihmisten kokonaismäärä, olipa se kaupunki, kaupunki, valtio tai maa. Otos on osa sitä väestöä

Tilastoissa väestön käsitteellä on laajempi merkitys kuin päivittäin. Väestö liittyy maan tai kaupungin asukkaiden lukumäärään, mutta tilastollinen väestö voi koostua elävistä ihmisistä ja olennoista, mutta myös suurista ja pienistä esineistä, hiukkasista, tapahtumista, tapahtumista ja ideoista.

Voi palvella sinua: Fourier -muunnos: Ominaisuudet, sovellukset, esimerkit

Esimerkkejä monipuolisista populaatioista ovat:

-Ilmamolekyylit suljetun astian sisällä.

-Kaikki tähdet Linnunradalla.

-Linnut, jotka asuttavat metsän.

Esimerkki ornitologeja tutkivasta väestöstä: metsän linnut

-Saman tai muun metsän puiden kokonaismäärä.

-Tilaajajoukko puhelinyhtiöllä, jolla on sivukonttoreita Amerikassa ja Euroopassa.

-Kolikosta tekemämme julkaisut.

-Bakteerien lukumäärä sato.

-Kuukausittainen ruuvien tuotanto tehtaalla.

väestöominaisuudet

Tiedämme jo, kuinka monipuoliset väestöt voivat olla. Katsotaan nyt, kuinka heidät voidaan luokitella laajennuksensa mukaan.

Rajallinen määrä on sellainen, joka voidaan ilmaista luvulla, kuten laatikossa olevien marmorien määrä. Toisaalta ääretön määrä emme voi antaa tarkkaa arvoa.

Tämä ero antaa meille mahdollisuuden määritellä kahden tyyppiset populaatiot niiden laajennuksen mukaan.

Äärelliset väestöt

Oletetaan, että laatikossa on 20 marmoria ja 2 marmorin näytteet uutetaan ilman korvaamista. Lopulta laatikon marmorit ovat uupuneet, joten väestö on rajallinen.

Luku voi olla rajallinen, vaikka se olisi erittäin suuri. Bakteeriviljelmä koostuu suuresta määrästä, mutta se on rajallinen, samoin kuin tähtien määrä galaksissa tai säiliöön lukitun kaasun molekyylien määrä.

Ääretön populaatio

Mitä tapahtuu, jos joka kerta kun otat marmorinäytteen, palautamme ne laatikkoon tarkkailun jälkeen? Siinä tapauksessa voimme saada äärettömän määrän näytteitä ja harkita siten, että marmoripopulaatio on ääretön.

Voi palvella sinua: kuusikulmainen prisma

Toinen esimerkki äärettömästä populaatiosta on kolikoiden tai noppan käynnistämisessä, koska teoriassa voit ottaa kaikki halutut näytteet ilman mitään rajaa.

Jopa tiedossa oleva rajallinen väestö sisältää paljon elementtejä, sitä voidaan tarvittaessa pitää käytännössä äärettömänä.

Siksi on erittäin tärkeää määritellä populaatio huolellisesti ennen tutkimuksen suorittamista, mikä tarkoittaa sen rajojen kiinnittämistä, koska sen koko määrittää siitä myöhemmin uutetun näytteen muodon ja koon.

Muut tärkeät ominaisuudet

On myös tärkeää tuntea väestön kronologinen sijainti. Ei ole sama tutkitaan suuren kaupungin alussa suuren kaupungin asukkaiden asiakirjoja kuin tehdä sama saman kaupungin asukkaiden kanssa 2000 -luvun alussa.

Analyytikon on myös huolehdittava väestön sijainnin huomioon ottamisesta ja heidän homogeenisuutensa tai sen puuttumisen selvittämisestä-.

Mikä on näyte?

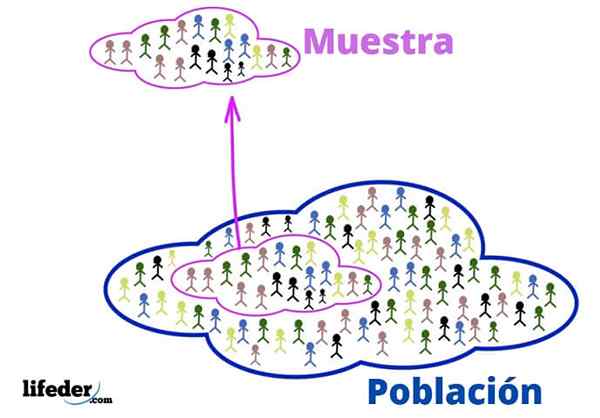Väestö ja otos

Otos on joukko valittuja elementtejä väestön keskuudessa edustamaan sitä. Tämän tekemisen tavoitteena on helpottaa työtä. Kun käsitellään vähemmän tietoja, vähemmän resursseja käännetään ja saadaan nopeampia tuloksia.

Näytteen on kuitenkin oltava riittävä. Valintaprosessi suoritetaan näytteenottotekniikoilla, jotka käyttävät matemaattisia kriteerejä.

Uuttuneen näytteen ei tarvitse olla ainutlaatuinen. Itse asiassa väestö voi johtaa erilaisiin näytteisiin.

Se voi palvella sinua: trigonometriset syyt: esimerkkejä, harjoituksia ja sovelluksia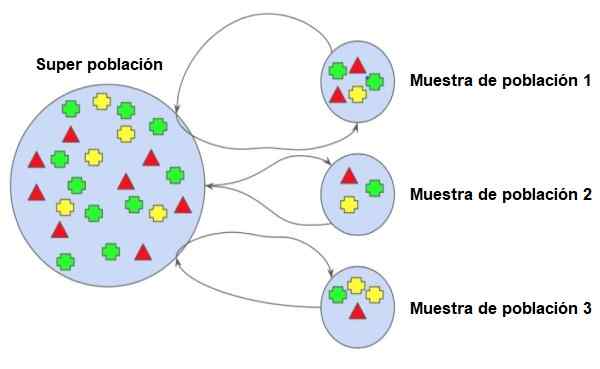 Erilaisia ​​näytteitä, jotka on uutettu populaatiosta. Lähde: Wikimedia Commons.

Oletetaan esimerkiksi, että väestö on joukko keskiasteen koulutuskeskuksen opiskelijoita, joilla on useita osioita jokaiselle luokalle. Edustavan näytteen tulisi sisältää joitain opiskelijoita kunkin tutkinnon jokaisesta osasta, esimerkiksi ne, joiden nimi alkaa kirjaimella A.

Toisaalta, ei niin edustava näyte voisi olla, jos kaikki saman asteen opiskelijat valittiin. Katsotaanpa lisää esimerkkejä:

Esimerkki 1

Tavaratalojen omistajat haluavat arvioida asiakkaiden käyttämän keskimääräisen rahan määrän. Tätä varten he keräävät kaikki tietyn ajanjakson laskut, sanotaan yhden vuoden.

Viime vuoden laskujen määrä on analysoitava väestö.

Nyt, jos tämä ryhmä on otettu täysin satunnainen näytte, jossa on 150 laskua, se olisi jo näyte.

Esimerkki 2

Kun vaalit lähestyvät, kansalliset tai paikalliset puolueet palkkaavat yleensä erikoistuneita yrityksiä tietojen analysointiin. Tällä tavoin he tietävät asukkaiden äänestyksen aikomuksen ja suunnittelevat asianmukaisia ​​kampanjastrategioita.

Tässä tapauksessa väestö koostuu koko äänestäjien maailmankaikkeudesta, jotka on rekisteröity vastaavassa vaalijärjestelmässä.

Koska jokaisen äänestäjän paikantaminen ja kuulustelu vie paljon aikaa ja vaivaa, kyselyt valitsevat näytteen äänestäjistä tutkimaan ja sieltä poimia prosenttiosuudet ja määrittävät trendit.

Asianmukaisen näytteen valinta on vasta alkua, mutta se on määräävä vaihe tutkimuksen menestyksen varmistamiseksi.

Viitteet

1. Berenson, m. 1985. Tilastot hallinnosta ja taloudesta, käsitteistä ja sovelluksista. Amerikanvälinen toimitus.
2. Brassi/rintakehä. 2009. Alittomat tilastot. Yhdeksäs. Painos. Hougton Mifflin.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Cengage -oppiminen.
4. Galindo, E. 2011. Tilastot, menetelmät ja sovellukset. Toimittajien prosessi.
5. Levin, r. 1981. Järjestelmänvalvojien tilastot. Prentice Hall.
6. Matemobili. Väestö ja otos, esimerkit ja harjoitukset. Toipunut: Matemovil.com.