Newtonin toinen lakihakemukset, kokeet ja harjoitukset

Se Newtonin toinen laki o Dynamiikan peruslaki toteaa, että jos esineeseen kohdistuu voima tai joukko voimia, joita ei ole kumota, niin esine kiihtyy tuloksena olevan voiman suuntaan, koska se kiihtyvyys on verrannollinen kyseisen nettovoiman intensiteettiin ja käänteisesti verrannollinen esineen massaan.

Joo F on nettovoima, M Esineen massa ja -lla Hänen hankkimansa kiihtyvyys, sitten Newtonin toinen laki ilmaistaan ​​matemaattisesti: -lla = F / M tai tavallisimmalla tavalla F = M∙-lla

Selitys Newtonin toisesta laista. Lähde: Itse tehty.

[TOC]

Selitys ja kaavat

Kuten edellä selitettiin, tavanomainen tapa ilmaista toinen laki on kaavan kanssa:

F = M∙-lla

Sekä kiihtyvyys että voima on mitattava inertiaalisesta vertailujärjestelmästä. Huomaa, että massa on positiivinen määrä, joten kiihtyvyyspisteet samaan suuntaan kuin tuloksena oleva voima.

Huomaa myös, että kun tuloksena oleva voima on tyhjä (F = 0 -) Sitten myös kiihtyvyys on mitätön ( -lla = 0 - ) niin kauan kuin M> 0. Tämä tulos on täysin samaa mieltä Newtonin ensimmäisen lain tai hitauslain kanssa.

Newtonin ensimmäinen laki vahvistaa inertiaaliset viittausjärjestelmät, kuten sellaiset, jotka liikkuvat jatkuvalla nopeudella vapaan hiukkasen suhteen. Käytännössä ja yleisimpien sovellusten tarkoituksena on kiinteä vertailujärjestelmä maahan tai muuhun, joka liikkuu vakiona nopeudella suhteessa siihen, pidetään inertiaalisesti.

Voima on esineen vuorovaikutuksen matemaattinen ilmaisu ympäristön kanssa. Voima voi olla vakio määrä tai muutos esineen ajan, sijainnin ja nopeuden myötä.

Kansainvälisen järjestelmän (SI) yksikkö on Newton (N). Massa (Si) mitataan (kg) ja kiihtyvyydessä (m/s²-A. Newton of Strength on välttämätön voima nopeuttaa 1 kg massaa 1 m/s² .

Ratkaisut

Harjoitus 1

Massa M -kohde vapautuu tietystä korkeudesta ja 9,8 m/s²: n syksyn kiihtyvyys mitataan.

Sama pätee toiseen massa massa m 'ja toinen massa m "ja toiseen. Tuloksena on aina painovoiman kiihtyvyys, joka on merkitty G: llä ja jonka arvo on 9,8 m/s². Näissä kokeissa esineen muoto ja sen massan arvo on sellainen, että ilmankestävyydestä johtuva voima on vähäinen.

Voi palvella sinua: kalsiumfluori (CAF2): rakenne, ominaisuudet, käyttötarkoitukset

Pyydetään etsimään malli maanpäälliselle vetovoimavoimalle (tunnetaan painona), joka on yhdenmukainen kokeellisten tulosten kanssa.

Ratkaisu

Valitsimme inertiaalisen vertailujärjestelmän (kiinnitetty lattiaan) pystysuoran X -akselin positiivisella suunnassa ja alas.

Ainoa joukko massaobjektilla m Se on maanpäällinen vetovoima, voimaa kutsutaan painoksi P, Kuinka se osoittaa, on positiivinen.

Massaobjektin hankkima kiihtyvyys m Kun se on julkaistu a = g , ja positiivinen.

Ehdotamme Newtonin toista lakia

P = m a

Mikä on P -malli siten, että toisen lain ennustama kiihtyvyys on G M: n arvosta riippumatta ? : Ainoa vaihtoehto on, että p = m g aina kun m> 0.

m g = m a Missä selvitämme: a = g

Johtopäätöksenä on, että paino, voima, jolla maa houkuttelee esinettä, on esineen massa kerrottuna painovoiman kiihtyvyydellä ja sen suunta on pystysuora ja kohdennettu.

P = m∙g

Harjoitus 2

2 kg: n massalohko lepää täysin sileässä ja vaakasuorassa lattiassa. Jos sovelletaan 1 n voima, kiihtyvyys saa lohkon ja mikä nopeus on yhden sekunnin kuluttua.

Ratkaisu

Ensimmäinen asia on määritellä inertiaalikoordinaattijärjestelmä. Yksi on valittu lattian X -akselilla ja akselilla ja kohtisuorassa siihen. Sitten tehdään voimakaavio, asettamalla voimat lohkon vuorovaikutuksen vuoksi sen ympäristön kanssa.

Voima P edustaa painoa, voimaa, jolla planeetta Earth houkuttelee massa m: n lohkoa.

Voima n edustaa normaalia, se on ylöspäin suuntautuva voima, jota lattian pinta käyttää lohkoon m. On tiedossa, että n tasapainottaa tarkalleen P: n, koska lohko ei liiku pystysuunnassa.

F on horisontaalinen voima, jota kohdistetaan lohkoon M, joka osoittaa X -akselin positiiviseen suuntaan.

Nettovoima on kaikkien joukkojen summa Mass M -lohkoon. F-, p- ja n: n summavektori tehdään. Koska p ja n ovat samat ja päinvastaiset, ne peruuttavat toisensa ja nettovoima on F.

Niin että tuloksena oleva kiihtyvyys on massa -nettovoiman osoitus:

Voi palvella sinua: Mekaaninen etu: Kaava, yhtälöt, laskenta ja esimerkit

A = f / m = 1 N / 2 kg = 0,5 m / s²

Kun lohko alkaa muusta 1S: n jälkeen, sen nopeus on vaihtunut 0 m/s nopeudella 0,5 m/s .

Newtonin toinen lakihakemus

Hissin kiihtyvyys

Poika käyttää kylpyhuonetta sen painon mittaamiseen. Saatu arvo on 50 kg. Sitten poika ottaa rakennuksensa hissin painon, koska hän haluaa mitata hissin kiihtyvyyden. Tulokset, jotka saadaan sen käynnistyessä, ovat:

• Asteikko tallentaa painon 58 kg 1,5 s
• Mittaa sitten taas 50 kg.

Laske näiden tietojen avulla hissin kiihtyvyys ja hankkimasi nopeus.

Ratkaisu

Asteikko mittaa painoa nimeltään yksikössä Kilogram_fuerza. Kilogram_fuerza on määritelmän mukaan voima, jolla planeetta maa houkuttelee 1 kg: n massaa.

Kun ainoa esineeseen vaikuttava voima on sen paino, se saa kiihtyvyyden 9,8 m/s². Joten 1 kg_f vastaa 9.8 n.

Paino P pojasta on sitten 50 kg*9.8m/s² = 490 N

Kiihtyvyyden aikana asteikko käyttää voimaa N 58 kg_f -poika, joka vastaa 58 kg * 9,8 m/s² = 568.4 n.

Hissin kiihtyvyys annetaan:

A = n/m - g = 568.4 N / 50 kg - 9.8 m/s² = 1.57 m/s²

Hissin hankkima nopeus 1 jälkeen.5 s 1 kiihtyvyydellä.57 m/s² on:

v = a * t = 1.57 m/s² * 1.5 s = 2.36 m/s = 8.5 km/h

Seuraava luku näyttää pojalle toimivien voimien kaavion:

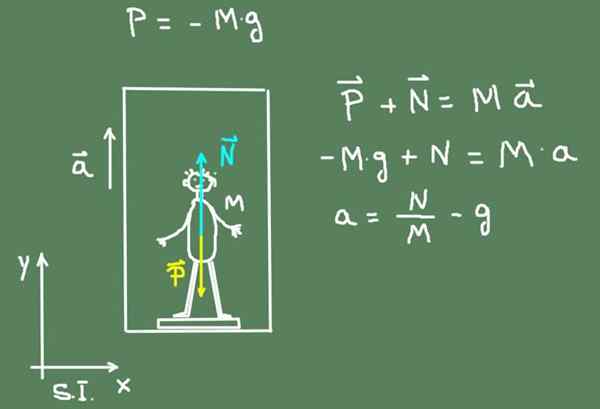
Majoneesipullo

Lapsi välittää veljensä pullon veljelleen, joka on pöydän toisessa päässä. Sillä se ajaa sitä siten, että se saa nopeuden 3 m/s. Koska pullo vapautetaan, kunnes se pysähtyy pöydän vastakkaiseen päähän, reitti oli 1,5 metriä.

Määritä taulukon pulloon kohdistuvan kitkavoiman arvo tietäen, että sen massa on 0,45 kg.

Ratkaisu

Ensin määrittelemme jarrukiihtyvyyden. Tätä varten käytämme seuraavaa suhdetta, joka tunnetaan jo tasaisesti kiihdytetylle suoraviivaiselle liikkeelle:

Vf² = v² + 2 * a * d

missä VF on viimeinen nopeus, Näin Alkuperäinen nopeus, -lla kiihtyvyys ja d -d Siirtymä.

Voi palvella sinua: dynaaminen sähkö

Edellisestä suhteesta saatu kiihtyvyys on, missä pullon siirtyminen on otettu positiiviseksi.

A = (0 - 9 (m / s) ²) / (2*1.5 m) = -3 m/s²

Majoneesipullon nettovoima on kitkavoima, koska pullon normaali ja paino on tasapainossa: fnet = kylmä.

Fr = m * a = 0.45 kg * (-3 m/s²) = -1.35 n = -0.14 kg-f

Lasten kokeet

Lapset ja aikuiset voivat myös tehdä yksinkertaisia ​​kokemuksia, joiden avulla he voivat varmistaa, että Newtonin toinen laki todella toimii tosielämässä. Tässä on kaksi mielenkiintoista hyvää:

Koe 1

Yksinkertainen kokeilu vaatii kylpyhuoneen ja hissin. Ota kylpyhuoneen paino hissiin ja kirjaa arvot, jotka merkitsevät nousun alkamisen, kengän alkamisen ja vakionopeuden aikana liikkuvan ajanjakson aikana. Laske kutakin tapausta vastaavan hissin kiihtyvyyttä.

Koe 2

1. Ota lelukori, jossa pyörät ovat hyvin voideltuja
2. Pidä köyttä äärimmäisyyteen.
3. Kiinnitä pöydän reunalla lyijykynä tai muu lieriömäinen ja sileä esine, jolla köys.
4. Köyden toisessa päässä roikkuu pieni kori, johon se sijoittaa kolikoita tai jotain, joka palvelee painoa.

Koejärjestelmä on esitetty alla:

• Vapauta kärry ja tarkkaile, kuinka se kiihtyy.
• Lisää sitten kärryn massaa asettamalla kolikoita siihen tai jotain, joka lisää sen massaa.
• Sano, jos kiihtyvyys kasvaa tai vähenee. Aseta enemmän taikinaa kärrylle, tarkkaile, kuinka se kiihtyy ja päättyy.

Sitten kärry jätetään ilman ylimääräistä painoa ja anna sen kiihtyä. Sitten koriin asetetaan enemmän painoa kärryyn kohdistetun voiman lisäämiseksi.

• Vertaa kiihtyvyyttä edelliseen tapaukseen, ilmoita, kasvaako se vai vähenee,. Voit toistaa lisäämällä koriin lisää painoa ja tarkkailla kärryn kiihtyvyyttä.
• Ilmoita, kasvaako se vai väheneekö se.
• Analysoi tulojasi ja sano ovatko he samaa mieltä Newtonin toisen lain kanssa.

Kiinnostavia artikkeleita

Esimerkkejä Newtonin toisesta laista.

Newtonin ensimmäinen laki.

Esimerkkejä Newtonin toisesta laista.

Viitteet

1. Alonso m., Suomalainen. 1970. Fysiikan osa I: Mekaniikka. Inter -American Educational Fund S.-Lla. 156-163.
2. Hewitt, s. 2012. Käsitteellinen fysiikka. Viides painos. 41-46.
3. Nuori, Hugh. 2015. Yliopiston fysiikka, jolla on moderni fysiikka. 14. ed. Pearson. 108-115.