Säännölliset monikulmioominaisuudet, elementit, kulmat, esimerkit

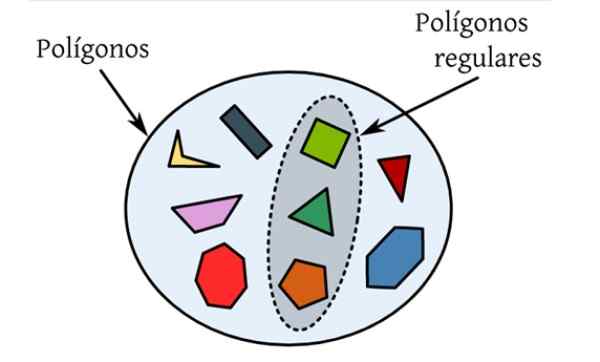
Se tavallinen monikulmikone He ovat niitä, joilla on kaikki puolensa ja tasa -arvoiset sisäiset näkökulmat. Seuraavassa kuvassa on joukko erilaisia ​​polygoneja, jotka ovat tasaiset kuviot, joita rajoittavat suljettu käyrä, ja vain korostetut vastaavat täyttävät olosuhteet säännöllisiksi.

Esimerkiksi tasa -arvoinen kolmio on tavallinen monikulmio, koska sen kolme sivua mittaavat samat, samoin kuin sen sisäkulmat, joiden arvo on 60 º, jokainen.

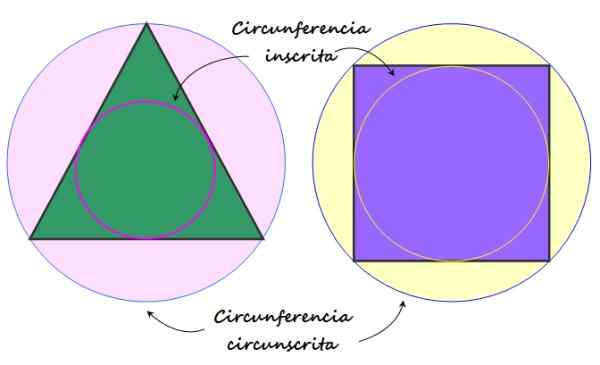
Kuvio 1. Säännölliset monikulmiot ovat niitä, joiden sivut ja sisäkulmat ovat samat, kuten tasapainon kolmio ja neliö. Lähde: Wikimedia Commons.

Neliö on nelikulmainen, jonka neljä sivua on yhtä suuri ja jonka sisäkulmat ovat 90º. Sitä seuraa tavallinen Pentagon, viisi sivua, joiden koko on yhtä suuri ja viisi sisäkulmaa 108º.

Kun monikulmio on säännöllinen, tämä sana lisätään sen erityiseen nimeen, joten meillä on tavallinen kuusikulmainen, tavallinen heptagon ja niin edelleen.

[TOC]

Tavallisten monikulmioiden ominaisuudet

Tavallisten monikulmioiden tärkeimmät ominaisuudet voidaan tiivistää seuraavasti:

-Sivut mittaavat saman, siksi ne ovat tasasivut.

-Are Tasa -arvoinen, No, kaikilla sen sisäkulmilla on yhtä suuri mitta.

-Ne voivat aina rekisteröidä kehässä, mikä tarkoittaa, että ne sopivat täydellisesti yhteen, jota kutsutaan ympärysmitta.

-N -sivujen tavalliselle monikulmiolle sisäkulman α mitta on:

α = [180 (n-2)]/n

-N-3)/2 diagonaalia voidaan piirtää monikulmion kärkipisteistä, riippumatta siitä, onko säännöllinen vai ei.

-Summa ulkokulmat Se on yhtä suuri kuin 360º.

Kuva 2. Rekisteröity keho ja ympärysmitta, jotka on rajoitettu tavalliselle monikulmiolle. Lähde: f. Zapata.

Tavallisen monikulmion elementit

Sitten esittelemme tavallisen monikulmion pääelementit, visualisoituna alempaan kuvaan.

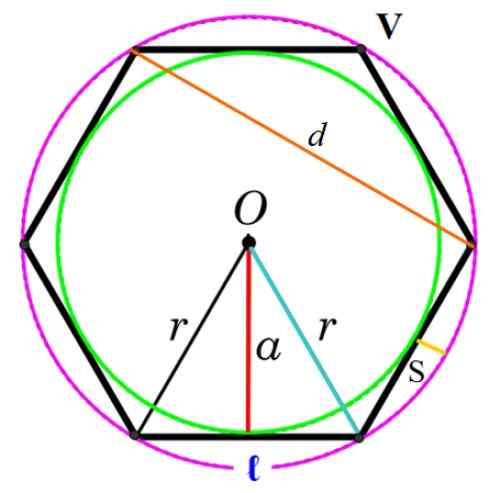Kuva 3. Tavallisen monikulmion elementit. Lähde: f. Zapata.

Kärki

Yleinen kohta, jolla on kaksi peräkkäistä puolta, merkittynä kuvassa V: ksi.

Sivu-

Segmentti liittyy monikulmion kahteen peräkkäiseen kärkipisteeseen ja on merkitty ℓ tai l.

Diagonaali

Segmentti, joka liittyy monikulmion kahteen ei -säilytyskuluun, kuvassa se on merkitty d -d.

Keskusta

Se on rekisteröidyn kehän yleinen keskus ja rajoitettu kehä, joka on merkitty kirjaimella tai. Sitä voidaan pitää myös ainoana pisteinä, että sekä kärkipisteiden että keskipisteiden etäisyys.

Radio

Se on radio r - rajoitetun ympärysmitasta ja osuu samaan aikaan O: n ja kärjen välisen etäisyyden kanssa.

Se voi palvella sinua: todennäköisyyden aksioomit: tyypit, selitys, esimerkit, harjoitukset

Apoteemi

Sitä kutsutaan apoteemi Polygoniin kirjoitetun kehän säteeseen, esitetty kuvassa kirjaimella -lla. Apoteemi on kohtisuorassa sivuun nähden ja yhdistää tämän keskustan O (punainen segmentti kuvassa 3).

Tietäen säteen R ja sivun pituuden, apoteemi lasketaan:

Koska käytännössä apoteemi on yksi suorakulmion kolmion luokista (katso kuva 3), toinen kateto on ℓ/2: n arvo (puolet toisesta puolesta) ja hypotenuse radio r - monikulmio.

Kun Pythagoras -lause sovelletaan mainittuun kolmioon, tämä yhtälö saadaan, mikä pätee paitsi kuusikulmioon, myös mihin tahansa tavalliseen monikulmioon.

Keskikulma

Se on kulma, jonka kärkipiste on samanaikainen keskustan kanssa tai joiden sivut ovat segmentit, jotka yhdistävät keskusta kahdella peräkkäisellä kärkipisteellä. Sen mitta seksuaalisesti on 360º/N, missä n Se on monikulmion sivujen lukumäärä.

Sagita

Se on ero monikulmion säteen ja apoteemin välillä (katso kuva 3). Merkitsee Sagitaa s:

S = r - a

Kehä ja alue

Kehä

Se lasketaan helposti lisäämällä sivujen pituudet. Koska mikä tahansa puoli on saman pituinen L ja siellä on n puolia, kehä P ilmaistaan ​​seuraavasti:

P = n.Lens

Alue

Tavallisessa monikulmiossa alue A antaa tuote puolipisteen (puolet kehästä) ja apotheme-pituuden välillä -lla.

A = p.A /2

Koska kehä riippuu sivujen lukumäärästä n, osoittautuu, että:

A = (NL).A /2

Kahdella tavallisella monikulmiolla voi olla sama kehä, vaikka niillä ei olisi samaa määrää sivuja, koska se riippuu sitten sivujen pituudesta.

Kirja V Kokoelma, Alexandrian matemaatikko Pappus (290-350), joka on viimeinen antiikin suurista kreikkalaisista matemaatikoista, osoitti, että kaikissa tavallisissa monikulmioissa, joilla on sama kehä, yksi, jolla on suurin alue, on suurin osa sivuista.

Kulmat

Kuvio 4 esittää tavanomaisessa monikulmiossa merkityksellisiä kulmia, jotka on merkitty kreikkalaisilla kirjaimilla α, β ja γ.

Keskikulma

Aikaisemmin mainitsemme keskikulman, tavallisen monikulmion elementtien joukossa, se on kulma, jonka kärki on monikulmion keskellä ja sivut ovat segmentit, jotka yhdistävät keskusta kahdella peräkkäisellä kärkipisteellä.

Keskikulman α mittauksen laskemiseksi 360º on jaettu n: llä, sivujen lukumäärä. Tai 2π radians välillä n:

Voi palvella sinua: injektiotoiminto: mistä se koostuu, mihin se on ja esimerkkejä

α = 360º/N

Radiaanien vastaava:

α = 2π /n

Sisäkulma tai sisäkulma

Kuviossa 4 Sisäinen kulma β on se, jonka kärkipiste on samanaikaisesti yhden kuvan ja sen sivut ovat myös kuvan sivut. Se on laskettu seksuaalisesti:

β = [180 (n-2)]/n

Tai radiaaneissa käyttämällä:

β = [π (n-2)]/n

Ulkokulmat

Ne merkitään kreikkalaisella kirjaimella γ. Kuvassa havaitaan, että y + β = 180º. Siksi:

γ = 180º - β

Kaikkien ulkoisten kulmien summa tavalliseen monikulmioon on 360º.

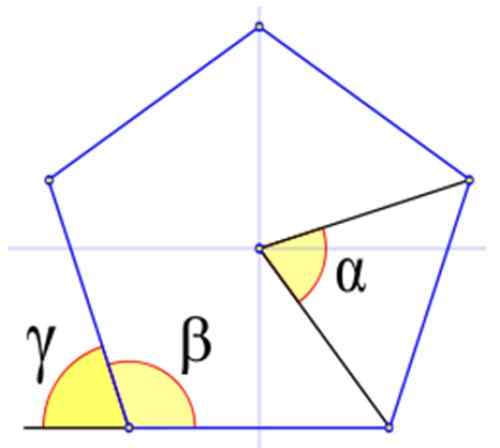Kuva 4. Kulmat tavallisessa monikulmiossa, tässä esimerkissä tavallinen Pentagon. Lähde: Wikimedia Commons.

Esimerkkejä tavallisista monikulmioista

Alla on 8 ensimmäistä säännöllistä monikulmiota. Huomaamme, että sivujen lukumäärän kasvaessa monikulmio muuttuu yhä enemmän keholle, jossa ne ovat rekisteröityneet.

Voimme kuvitella, että sivujen pituuden tekeminen yhä pienemmäksi ja lisäämällä näiden lukumäärää, saamme kehän.

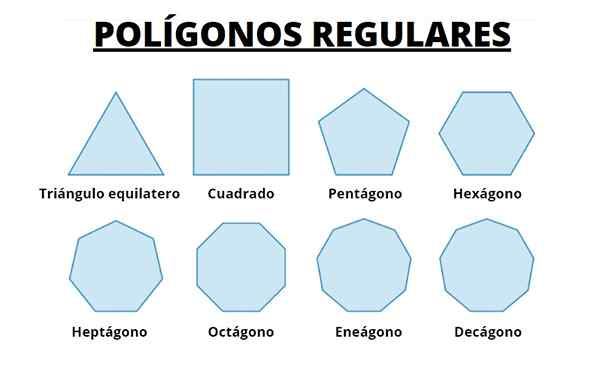Kuva 5. Kahdeksan ensimmäistä tavallista monikulmiota. Lähde: Wikimedia Commons.

- Säännölliset monikulmiot jokapäiväisessä elämässä ja luonnossa

Säännöllisiä monikulmioita löytyy kaikkialta jokapäiväisessä elämässä ja jopa luonnossa. Katsotaanpa joitain esimerkkejä:

Liikennemerkit

Valtatiellä ja teillä näemme merkinnöissä runsaasti säännöllisiä monikulmioita, kuten tasa -arvoisia, neliö- ja rhombus -kolmioita. Kuvassa 6 näemme korkean muotoisen signaalin signaalin.

Kuva 5.- Liikenteen signaali kahdeksankulmaisella muodolla. Lähde: Pixabay.

Huonekalut

Lukemattomat huonekalukappaleet ovat esimerkiksi neliömäisiä tyypillisenä geometrisena hahmona, samoin kuin monet pöydät, tuolit ja pankit ovat neliöitä. Rinnakkaispiped on yleensä laatikko, jossa on suorakaiteen muotoiset sivut (mikä ei ole tavallinen monikulmio), mutta ne voivat myös tehdä neliön.

Arkkitehtuuri ja rakentaminen

Lattioiden ja seinien laatat tai laatat, sekä kodeissa että kaduilla, on usein tavallisten monikulmioiden muoto.

Teselit ovat pintoja, jotka on peitetty kokonaan laattoilla, joilla on monipuolisia geometrisia lukuja. Kolmion kanssa neliö ja kuusikulmio voidaan tehdä säännöllisistä tiloista, jotka käyttävät vain yhden tyyppistä hahmoa pinnoitteen täydellisesti, ilman tyhjiä välilyöntejä (katso kuva 6).

Myös rakennukset hyödyntävät säännöllisiä monikulmioita elementteissä, kuten Windows ja sisustus.

Kuva 6. Neliömäinen laatta. Lähde: Pixabay.

- Säännölliset kuusikulmiot luonnossa

Yllättäen tavallinen kuusikulmio on monikulmio, joka esiintyy usein luonnossa.

Voi palvella sinua: Diskreetti jakauma

Mehiläisten hunajan hunajakennoilla on erittäin likimääräinen muoto tavalliseen kuusikulmioon. Kuten Alexandrian pappus havaitsi, mehiläiset optimoivat tällä tavalla tilaa säästääksesi niin paljon hunajaa kuin mahdollista.

Ja kilpikonnien ja lumihiutaleiden kuoressa on myös säännöllisiä kuusikulmioita, jotka myös omaksuvat erilaisia ​​erittäin kauniita geometrisia muotoja.

Liikuntaa

Tavallinen kuusikulmio on osa 6 cm: n säteen puolipyöreä, kuten kuvassa esitetään. Mikä on varjostetun alueen arvo?

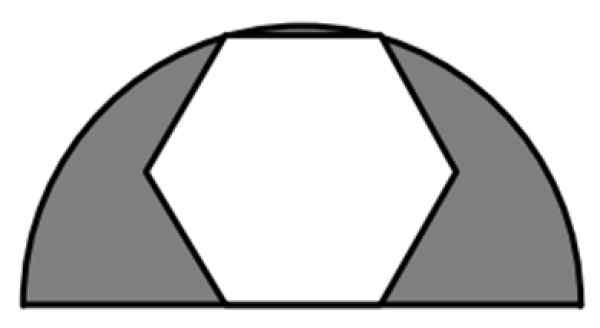Kuva 7. Säännöllinen kuusikulmio on rekisteröity puolipyöreään. Lähde: f. Zapata.

Ratkaisu

Varjostettu alue on ero säteen puolipyöreän pinta -alan r = 6 cm ja koko kuusikulmio -alueen, tavallisen 6 -puolueen monikulmion välillä. Joten tarvitsemme kaavoja näiden lukujen alueelle.

Puolipyöreä alue

-Lla₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Säännöllinen kuusikulmioalue

Kaava tavallisen monikulmion alueen laskemiseksi on:

A = p.A /2

Missä P Se on kehä ja -lla Se on apoteemi. Koska kehä on sivujen summa, tarvitsemme näiden arvon. Tavalliselle kuusikulmiolle:

P = 6ℓ

Siksi:

A = 6ℓA /2

Sivun arvon löytämiseksi ℓ on välttämätöntä rakentaa apulahjat, jotka selitämme alla:

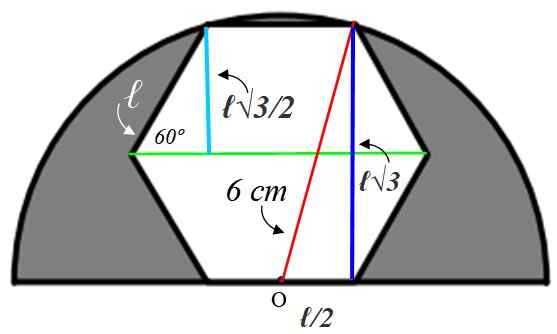
Aloitetaan pienellä suorakulmiokolmiolla vasemmalle, jonka hypotenuse on ℓ. Kuusikulmion sisäkulma on arvoinen:

α = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120º

Säde, jonka olemme piirtäneet bisektavihreäksi, tämä kulma, joten pienen kolmion akuutti kulma on 60º. Annetulla tiedoilla tämä kolmio on ratkaistu, löytää vaaleansininen puoli, joka mittaa sama kuin apotemi:

Vastakkainen cateto = a = ℓ x sin 60º = ℓ√3 / 2 cm

Tämä arvo on kaksinkertainen suuren kolmion tummansininen jalka oikealle, mutta siitä kolmiosta tiedämme, että hypotenusen mitat ovat 6 cm, koska se on puolipyörän säde. Jäljellä oleva kateto (alla) on arvoinen ℓ/2, koska pisteen tai on puolen keskellä.

Koska tämän kolmion sisäkulmista ei tunneta, voimme nostaa hänelle Pythagoras -lauseen:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Tällä arvolla apoteemi lasketaan:

A = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Soitetaan a₂ Tavalliselle kuusikulmioalueelle:

= 28. 8 cm²

Varjostettu hahmoalue

-Lla₁ - -Lla₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Viitteet

1. Baldor, a. 1973. Geometria ja trigonometria. Keski -Amerikan kulttuuritoimitus.
2. Nauti matematiikasta. Kiput. Toipunut.com.
3. JA. -Lla. 2003. Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
4. Kuusikulmioon luonteeltaan. Toipunut: Malvargamath.WordPress.com.
5. Jiménez, r. 2010. Matematiikka II. Geometria ja trigonometria. Toinen painos. Prentice Hall.
6. Tavallinen monikulmikone. Toipunut: kaveri.tekniikka.USAC.Edu.GT.
7. Wikipedia. Apoteemi. Palautettu: on.Wikipedia.org.