Manometrinen paine selitys, kaavat, yhtälöt, esimerkit

Se mittaripaine P_m Se on mitattu suhteessa vertailupaineeseen, joka on useimmissa tapauksissa valittu ilmakehän paine P_{Pankkiautomaatti} merenpinnassa. Se on sitten a Suhteellinen paine, Toinen termi, jolle se on myös tiedossa.

Toinen tapa, jolla paine yleensä mitataan. Tässä tapauksessa puhuu absoluuttinen paine, johon tarkoitamme kuinka p_-lla.

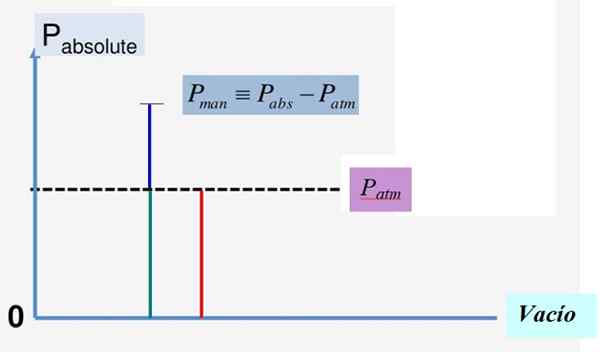
Kuvio 1. Absoluuttinen paine ja manometrinen paine. Lähde: f. Zapata.

Näiden kolmen määrän välinen matemaattinen suhde on:

P_-lla = P_{Pankkiautomaatti} + P_m

Siksi:

P_m = P_-lla - P_{Pankkiautomaatti}

Kuva 1 kuvaa kätevästi tätä suhdetta. Koska tyhjiöpaine on 0, absoluuttinen paine on aina positiivinen ja sama koskee ilmakehän painetta p_{Pankkiautomaatti}.

Manometristä painetta käytetään yleensä ilmakehän paineen yläpuolella olevien paineiden merkitsemiseen, kuten renkaiden tai meren tai uima -altaan alaosassa olevaan kannettaviin siihen, jota vesipylvään paino käyttää. Näissä tapauksissa p_m > 0, p -koska p_-lla > P_{Pankkiautomaatti}.

P: n alla on kuitenkin absoluuttisia paineita_{Pankkiautomaatti}. Näissä tapauksissa p_m < 0 y recibe el nombre de tyhjiöpaine Eikä sitä pidä sekoittaa jo kuvattujen tyhjiöpaineeseen, joka on hiukkasten puuttuminen, jotka kykenevät käyttämään paineita.

[TOC]

Kaavat ja yhtälöt

Paine neste- tai kaasu- ja kaasupaine on yksi sen tutkimuksen merkittävimmistä muuttujista. Paikallisessa nesteessä paine on sama kaikissa pisteissä samaan syvyyteen suuntautumisesta riippumatta, kun taas putkien nesteiden liikkuminen johtuu paineen muutoksista.

Keskimääräinen paine määritellään osamääräksi kohtisuoraan pintaan F_⊥ ja mainitun pinnan A alue, joka ilmaistaan ​​matemaattisesti seuraavasti:

P = f_⊥ /

Paine on skalaarinen määrä, jonka mitat ovat voimaa aluetta kohti. Mittauksen yksiköt kansainvälisissä yksiköissä (SI) ovat Newton/M², kutsutaan Pascaliksi ja lyhennettynä PA: ksi Blaise Pascalin kunniaksi (1623-1662).

Moninkertaistaa kuten kilo (10³) ja mega (10⁶) Niitä käytetään usein, koska ilmakehän paine on yleensä välillä 90.000 - 102.000 PA, joka on yhtä suuri kuin: 90 - 102 kPa. Mega Pascals -järjestyksen paineet eivät ole harvinaisia, joten on tärkeää perehtyä etuliitteisiin.

Anglo -saksonyksiköissä paine mitataan kilona/jalka², Yleinen asia on kuitenkin tehdä puntaa/tuumaa² jompikumpi psi (Punta-voima neliötuumaa kohti-A.

Voi palvella sinua: Lämmönsiirto: lait, lähetyslomakkeet, esimerkit

Paineen vaihtelu syvyydellä

Mitä enemmän upotamme uima -altaan veteen tai mereen, sitä enemmän painostustamme koemme. Päinvastoin, lisääntyvä korkeus, ilmakehän paine laskee.

Keskimääräinen ilmakehän paine merenpinnassa on määritetty 101300 PA: ssa tai 101.3 kPa, vaikka Mariana -kuopassa Länsi -Tyynellämerellä - suurin tiedossa oleva syvyys - se on noin 1000 kertaa korkeampi ja Everestin yläosassa on vain 34 kPa.

On selvää, että paine ja syvyys (tai korkeus) liittyvät. Lepo -nesteen (staattisen tasapainon) tapauksessa sitä pidetään nesteosana, jossa on levyn muotoinen neste, joka on rajoitettu säiliöön (katso kuva 2). Levyllä on poikkileikkaus -Lla, paino Dw ja korkeus Dy.

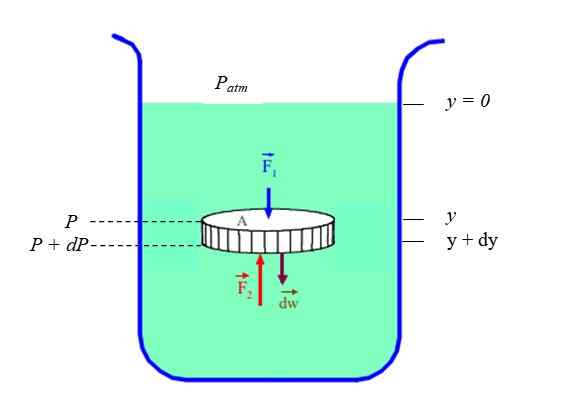Kuva 2. Staattisen tasapainon nesteen differentiaalielementti. Lähde: Fanny Zapata.

Soitamme P Paineessa, joka on syvällisesti "ja"ja P + DP Paineessa, joka on syvyydessä (ja + dy-A. Koska nesteen tiheys ρ on syy sen massan välillä Dm ja sen tilavuus DV, Sinun täytyy:

ρ = DM/ DV ⇒ DM = ρ.DV

Siksi paino Dw elementti on:

dw = g. Dm = ρ.g.DV

Ja nyt Newtonin toista lakia sovelletaan:

Σ f_ja = F₂ - F₁ - Dw = 0

(P + DP).A - P.-Lla - ρ.g.DV = 0

(P + DP).A - P.-Lla - ρ.g. -Lla. Dy = 0

DP = ρ.g.Dy

Differentiaaliliuos 

Integroida molemmat osapuolet ja ottaen huomioon tiheys ρ, samoin kuin painovoima g Ne ovat vakioita, on haluttu ilmaus:

P₂ - P₁ = ΔP = ρ.g.(ja₂ - ja₁-A

ΔP = ρ.g. Δja

Jos edellisessä lausekkeessa se valitaan P₁ kuten ilmakehän paine ja ja₁ Kuten nesteen pinta, sitten ja₂ Se sijaitsee syvyydessä h ja ΔP = P₂ - P_{Pankkiautomaatti} Se on manometrinen paine syvyydestä riippuen:

P_m = ρ.g.h

Jos tarvitset absoluuttisen paineajan, ilmakehän paine lisätään yksinkertaisesti edelliseen tulokseen.

Esimerkit

Manometriselle painemittalle laitetta käytetään painemittari, jotka yleensä tarjoavat paine -eroja. Loppujen lopuksi kuvataan U -jaettujen paineen manometrin toimintaperiaate, mutta katsotaan nyt joitain tärkeitä esimerkkejä ja seurauksia aiemmin vähennettynä yhtälöllä.

Pascal -periaate

Yhtälö ΔP = ρ.g.(ja₂ - ja₁-A Se voidaan kirjoittaa  P = po + ρ.g.h, missä P on paine syvyydessä h, sillä aikaa P_jompikumpi Se on nesteen pinnan paine, yleensä P_{Pankkiautomaatti}.

Ilmeisesti joka kerta kun kasvatat Poikki, kasvaa P Samassa määrässä, niin kauan kuin se on neste, jonka tiheys on vakio. Juuri sen piti harkita ρ vakio ja aseta se edellisessä osassa ratkaistu kiinteän aineen ulkopuolelle.

Voi palvella sinua: yksinkertainen harmoninen liike

Pascal -periaatteessa todetaan, että mikä tahansa tasapainossa rajoitetun nesteen paineen nousu, välittyy ilman mitään variaatiota kaikkiin mainitun nesteen pisteisiin. Tämän ominaisuuden kautta on mahdollista moninkertaistaa voima F₁ levitetään vasemmalle vasemmalle ja hanki F₂ oikealla.

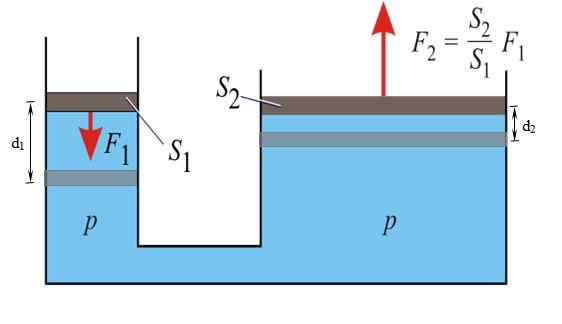Kuva 3. Hydraulisessa puristimessa käytetään Pascal -periaatetta. Lähde: Wikimedia Commons.

Autojarrut toimivat tämän periaatteen mukaisesti: Polkimiin kohdistetaan suhteellisen pieni voima, josta tulee merkittävä voima jarrusylinteriin jokaisella pyörällä, järjestelmässä käytetyn nesteen ansiosta.

Stevinin hydrostaattinen paradoksi

Hydrostaattinen paradoksi toteaa, että säiliön pohjassa olevan nesteen paineesta johtuva voima voi olla yhtä suuri, suurempi tai pienempi kuin itse nesteen paino. Mutta laittamalla säiliö asteikon päälle, se tallentaa yleensä nesteen painon (plus yksi säiliöstä tietysti). Kuinka selittää tämä paradoksi?

Aloitamme siitä tosiasiasta, että säiliön alaosassa oleva paine riippuu yksinomaan syvyydestä ja on riippumaton muodosta, kuten edellisessä osassa päätelty.

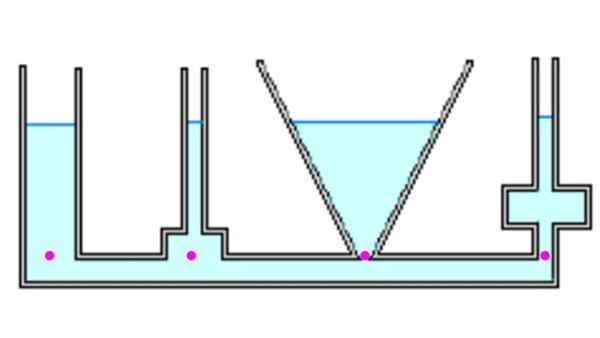Kuva 4. Neste saavuttaa saman korkeuden kaikissa astioissa ja taustalla oleva paine on sama. Lähde: f. Zapata.

Katsotaanpa joitain erilaisia ​​astioita. Kun ne on ilmoitettu, kun ne on täytetty nesteellä, kaikki saavuttavat saman korkeuden h. Näkyvät kohdat ovat samassa paineessa, koska ne ovat samassa syvyydessä. Jokaisessa pisteessä olevasta paineesta johtuva voima voi kuitenkin poiketa painosta (katso esimerkki 1 alla).

Harjoitukset

Harjoitus 1

Vertaa voimaa, jota paine kohdistuu kunkin astian pohjaan nesteen painon kanssa, ja selitä miksi erot, jos niitä on.

Säiliö 1 

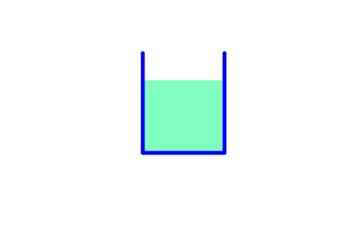Kuva 5. Paine taustalla on sama nesteen painon suhteen. Lähde: Fanny Zapata.

Tässä astiassa perusalue on, siksi:

Nesteen paino: mg = ρ.V.G = ρ . -Lla .h . g

Paine pohjaan: ρ. g. h

Paineesta johtuva voima: f = P.A = ρ. g. h. -Lla

Paineesta aiheutuva paino ja voima ovat yhtä suuret.

Säiliö 2 

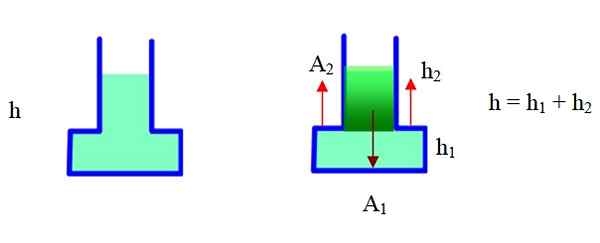Kuva 6. Tämän säiliön paineesta johtuva voima on suurempi kuin paino. Lähde: f. Zapata.

Kontissa on kapea osa ja laaja osa. Oikeassa järjestelmässä se on jaettu kahteen osaan ja käyttää geometriaa kokonaistilavuuden löytämiseen. Alue a₂ on säiliön ulkopuolella, h₂ Se on kapean osan korkeus, h₁ Se on leveän osan korkeus (pohja).

Voi palvella sinua: Pleiades: historia, alkuperä ja koostumus

Koko äänenvoimakkuus on emäksen tilavuus + kapean osan tilavuus. Näiden tietojen kanssa:

Nesteen paino: m . G = ρ . g. V = ρ . g. [₁ .h₁+ (₁ --Lla₂-A .h₂] =

= ρ . g (a₁.haita₂h₂) = ρ . g . -Lla₁.H - ρ . g . -Lla._. h₂ (Käyttö h = h₁ +h₂-A

Paine pohjassa: p = ρ. g. h

Voima alareunassa paineesta: f = P. -Lla₁ = ρ. g. h. -Lla₁

Vertaamalla nesteen painoa voimaan painosta johtuen on huomattava, että tämä on suurempi kuin paino.

Tapahtuu se, että neste myös lisää askeleen askelta (katso kuvan punaiset nuolet), jotka sisältyvät edelliseen laskelmaan. Tämä torjunta -asemat ovat alhaalla ja asteikolla tallennettu paino on näiden seurausta. Tämän mukaan painon suuruus on:

W = voima taustalla - vahvuus porrastetussa osassa = ρ . g . -Lla₁.H - ρ . g . -Lla._. h₂

Harjoitus 2

Kuva näyttää avoimen putken painemittarin. Se koostuu U -putkesta, jossa yksi päistä on ilmakehän paineessa ja toinen liittyy S: hen, järjestelmään, jonka paine mitataan.

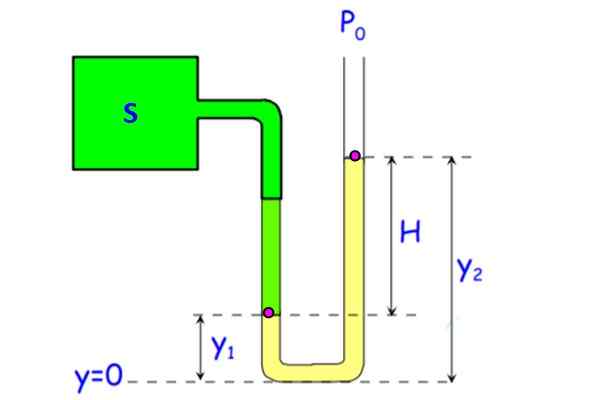Kuva 7. Avoin putken painemittari. Lähde: f. Zapata.

Putken neste (kuvassa keltainen) voi olla vettä, vaikka elohopeaa käytetään laitteen koon pienentämiseen. (Ero 1 ilmapiiri tai 101.3 kPa vaatii 10 vesipylvään.3 metriä, ei mitään kannettavaa).

Manometrinen paine pyydetään löytämään P_m S -järjestelmässä nestepylvään korkeudesta H riippuen.

Ratkaisu

Putken molemmille oksille taustalla oleva paine on sama, sillä se on samassa syvyydessä. Anna p_-Lla Paine pisteessä A, joka sijaitsee ja₁ Ja p_{B -} pisteiden B, joka on korkeudessa ja₂. Koska kohta B sijaitsee neste- ja ilma -rajapinnassa, paine on P_jompikumpi. Tässä painemittari -haarassa alareunassa oleva paine on:

PO + ρ.g.ja₂

Vasemman haaran alareunassa oleva paine puolestaan ​​on:

P + ρ.g.ja₁

Missä p on järjestelmän absoluuttinen paine ja ρ on nesteen tiheys. Yhtä suuri kuin molemmat paineet:

PO + ρ.g.ja₂ = P +ρ.g.ja₁

Puhdistus P-

P = po + ρ.g.ja₂ - ρ.g.ja₁ = Po + ρ.g (ja₂ - ja₁) = Po + ρ.g. H

Siksi manometrinen paine P_m Se on annettu P - p_jompikumpi = ρ.g. H Ja sen arvon saamiseksi riittää mittaamaan korkeus, johon manometrinen neste nousee, ja moninkertaistaa sen arvolla g ja nestetiheys.

Viitteet

1. Cimbala, c. 2006. Nesteiden, perusteiden ja sovellusten mekaniikka. MC. Graw Hill. 66-74.
2. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Fluidimekaniikka. Neljäs. Painos. Pearson -koulutus. 53-70.
4. Shaugnessy, E. 2005. Johdanto nestemekaniikkaan.Oxford University Press. 51 - 60.
5. Stylianos, V. 2016. Yksinkertaiseen selitykseen klassisesta hydrostaattisesta paradoksista. Toipunut: Haimgaifman.Tiedostot.WordPress.com