Ensimmäinen tasapainon kunto Selitys, esimerkit, harjoitukset

Se Ensimmäinen tasapainon kunto Se edellyttää, että kaikkien vartaloon vaikuttavien voimien runsasvektori on tyhjä, niin että se on levossa (staattinen tasapaino) tai yhtenäisellä suorakulmaisella liikkeellä (dynaaminen tasapaino).

Tämä voimien summa ei ole kukaan muu kuin kehoon vaikuttava nettovoima, joka ilmaisee tämän moodin matemaattisesti:

F_Netto = 0 -

∑ F = 0 -

Kuvio 1. Antiikin rakentajat ovat jo soveltaneet ensimmäistä tasapainoolosuhteita, kuten käy ilmi Stonehenge -muistomerkissä. Lähde: Pixabay.

Avaruudessa ensimmäinen tasapainotila antaa kolme yhtälöä, yksi jokaiselle ulottuvuudelle:

∑ f_x = 0; ∑ f_ja = 0 ja ∑ f_{z -z} = 0

Kun nämä yhtälöt täyttyvät, esine ei liiku tai jos se tapahtuu, se on vakiona nopeudella.

Tarkkailemalla ympärillämme ymmärrämme, että pyrimme jatkuvasti täyttämään ensimmäisen tasapainon ehdon niin, että asiat eivät pudota.

Siksi sillä pyritään kompensoimaan maan gravitaatiota vetovoiman tuella, köysillä tai tukien avulla, jotta asiat pysyvät paikoillaan eivätkä mene maahan.

Muina aikoina tarvitaan estää ulkoisia sähkömagneettisia kenttiä häiritsemästä sähköpiirien ja viestintälaitteiden toimintaa. Tällöin sähkövarat on oltava tasapainossa.

[TOC]

Esimerkit

Suuri määrä arjen esineitä täyttää ensimmäisen tasapainotilan, kyse on huolellisesti tarkkailusta:

Rakennukset

Rakentajat etsivät rakennusten vakautta, jotta käyttäjät pysyvät turvassa. Staattisen tavoitteena on tutkia rakennusten, siltojen, teiden ja kaikenlaisten rakenteiden staattisen tasapainon olosuhteita.

Higafoorit ja roikkuvat varoitukset

Näiden signalointilaitteiden on pysyttävä kiinteinä toimintojensa suorittamiseksi, joten niihin sovelletaan kaapeleita, pylväitä ja sauvoja siten, että ensimmäinen saldo -ehto täyttyy.

Se voi palvella: Kolmas termodynamiikan laki: kaavat, yhtälöt, esimerkitKuva 2. Liikennevalot ja roikkuvat varoitukset ovat kohteena siten, että se täyttää ensimmäisen tasapainon olosuhteet. Lähde: PxFuel.

Sähkötasapainon kuljettajatkattohuoneisto

Kun johtavat materiaalit, kuten kupari ja muut metallit, hankkivat sähkövarauksen, sähköstaattinen tasapaino on pian muodostettu, jättäen kuormitusylijäämää johtavalle pinnalle. Sähkökentän sisällä on nolla.

Tätä vaikutusta käytetään usein ulkoisten kenttien sähkö- ja elektronisten laitteiden eristämiseen SO -nimisen Faraday -häkin avulla. Häkki on valmistettu johtavasta materiaalista ja ympäröi suojattavia laitteita.

Myrskyjen aikana autot palvelevat kuin Faraday -häkit suojaamalla matkustajia sähköisiltä iskuilta.

Kattovalaisimet

Valaistusjärjestelmissä, kuten ripustetut lamput, ensimmäistä tasapainoolosuhteita käytetään niiden kiinnittämiseen katolle, lattiaan tai seinään.

Kuva 3. Läpiläiset, nimeltään "Hämähäkit", tyydyttää ensimmäisen tasapainon olosuhteet. Lähde: Pixabay.

Kirjat ja esineet pöydissä

Taulukoihin ja hyllyihin asetetut esineet täyttävät ensimmäisen tasapainon kunto. Normaali voima, jota tuella on esineitä, vastaa painon korvaamisesta.

Nesteen viskositeetin mitta

Nesteen viskositeetin määrittämiseksi pallomainen kohde, tunnetun halkaisijan, joka näkee sen nopeuden, koska vastus on pudonnut sisälle. Pallon nopeus on vakio, dynaamisessa tasapainossa.

Nesteen suurempi viskositeetti, vähemmän nopeus, jolla pallo liikkuu sisälle.

Vaiheet ensimmäisen tasapainoolosuhteen soveltamiseksi

-Tee vapaa kehon kaavio, joka näyttää kaikki ruumiissa toimivia voimia (jätä se, mitä vartalo käyttää muille).

Se voi palvella sinua: fysiikka keskiajalla

-Valitse Cartesian koordinaattijärjestelmä varmistaen, että jos mahdollista, voimat sijaitsevat millä tahansa akselilla. Positiivinen osoite otetaan yleensä liikkeen merkityksessä tai mahdollisessa liikkeessä.

-Määritä kunkin voiman Cartesian -komponentit.

-Käytä Newtonin toista lakia jokaiselle komponentille, sellaisena kuin se on perustettu, on yhtälöjärjestelmä.

-Ratkaise edellisessä vaiheessa nostettu yhtälöjärjestelmä.

Ratkaisut

- Liikunta ratkaistiin 1

Kuvion lohko, massa m, Se liikkuu alamäkeen kulmatasolla θ vakiona nopeudella. Laske kineettisen kitkan μ -kertoimen arvo_{k -k -}, Jos lohkon massa on M = 5 kg ja θ = 37º.

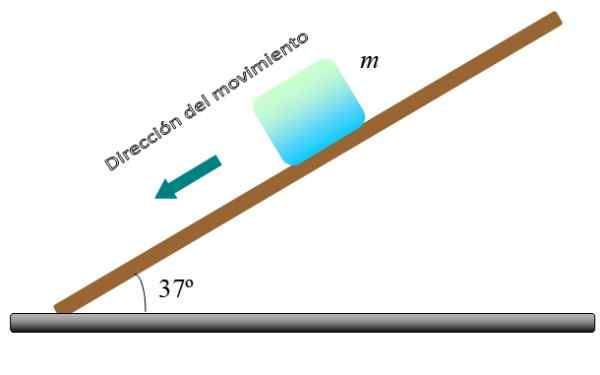Kuva 4. Lohko liukuu vakiona nopeudella kaltevalla tasolla. Lähde: f. Zapata.

Ratkaisu

Ensimmäinen askel on piirtää vapaa kehon kaavio ja valita Cartesian -koordinaattijärjestelmä jokaisen voimavektorin ilmaisemiseksi. Lohkoon vaikuttavat voimat ovat:

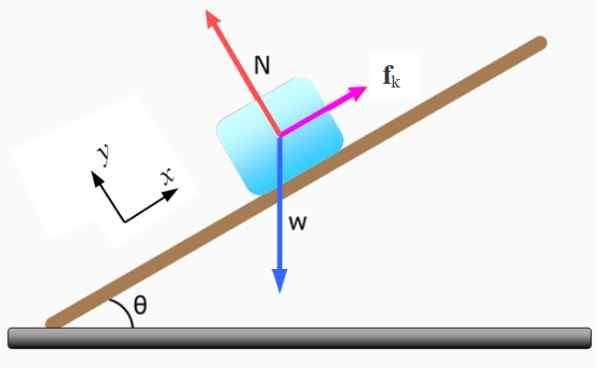Kuva 5. Ilmainen runkokaavio lohkolle. Lähde: f. Zapata.

-Normaali N kaltevan tason harjoittama, se on kohtisuorassa tämän pintaan.

-Paino W - Se on suunnattu pystysuoraan.

-Kineettinen kitka F_{k -k -} joka vastustaa liikettä. Jos sitä ei olisi, vartalo liikkuu alamäkeen kiihtyvyydellä g.Sentr.

Kuin paino W - Se on kalteva valittujen koordinaattiakselien suhteen, se on jaottava Cartesian -komponentteihinsa:

W -_x = mg.SEN 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
W -_ja = mg.cos 37º = 5 kg x 9,8 m/s² x cos 37º = 39.1 n

Newtonin toista lakia sovelletaan nyt, mikä vastaa jokaista summaa 0: een, koska lohkolla ei ole kiihtyvyyttä liikkuessaan jatkuvalla nopeudella:

∑ f_ja = N - w_ja = 0
∑ f_x = W_x - F_{k -k -} = 0

Kineettisen kitkan suuruus on verrannollinen normaalin suuruuteen, joka on kineettinen kitkakerroin μ_{k -k -} Suhteellisuusvakio.

Se voi palvella sinua: Absoluuttinen paine: kaava, miten se lasketaan, esimerkkejä, harjoituksia

F_{k -k -} = μ_{k -k -} N

Samaan aikaan:

N = w_ja = 39.1 n

Ja myös:

F_{k -k -} = W_x

Siksi:

29. 5 n = μ_{k -k -} X 39.1 n

μ_{k -k -} = 29. 5/39.1 = 0.75

- Liikunta ratkaistiin 2

Laske niiden jännitteiden suuruus, jotka tukevat massaliikennevaloa 33 kg, kuvassa:

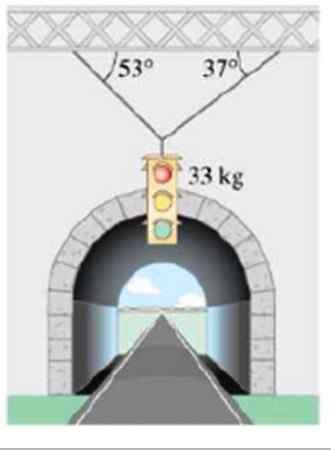Kuva 6. Liikennevalo roikkuu kaapeleilla. Lähde: Giancoli. Fysiikka sovelluksilla.

Ratkaisu

Vapaa kehon kaavio tehdään sekä liikennevalolle että kaapeleita pitävälle solmuksille:

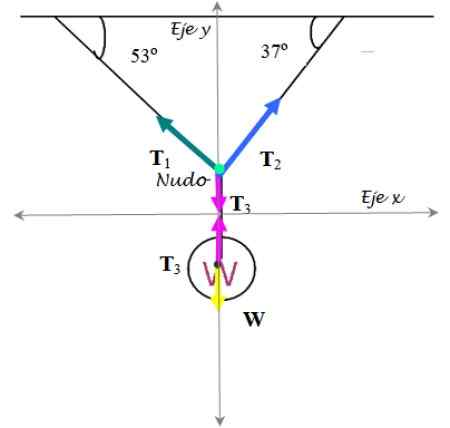Kuva 7. Vapaa kehon kaavio liikunnasta ratkaistu 2. Lähde: f. Zapata.

Liikennevalo

Siitä ACT: Jännitys t₃ ylös ja paino w alas. Siksi:

∑ f_ja = W - t₃ = 0

Siksi:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Solmu

Jännitteet hajoavat heidän Cartesian -komponenteissaan:

∑ f_ja = T₁ Sen 53º + t₂ SEN 37º - t₃ = 0
∑ f_x = T₂ Cos 37º - t₁ Cos 53º = 0

Ja saadaan seuraava lineaaristen yhtälöiden järjestelmä, jossa on kaksi tuntematonta₁  ja T₂ -

- 0 -.6 t₁ + 0 -.8 t₂ = 0
0 -.8 t₁ + 0 -.6 t₂ = 323.4

Tämän yhtälöjärjestelmän ratkaisu on: t₁ = 258.7 n ja t₂ = 194.0 N

Kiinnostavia teemoja

Tasapainoolosuhteet.

Toinen tasapainotila.

Viitteet

1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Hiukkasjärjestelmät. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Wikipedia. Staattinen (mekaaninen). Palautettu: on.Wikipedia.org.