Suhteelliset serkut mitkä ovat, selitys, esimerkkejä

Kutsutaan suhteelliset serkut (Coprmimos tai serkut suhteessa toisiinsa) mihin tahansa kokonaislukupariin, joilla ei ole yhteistä jakajaa, paitsi 1. Toisin sanoen, kaksi kokonaisluku on suhteellisia serkkuja, jos niiden jakautumisensa alaryhmissä heillä ei ole yhteistä tekijää.

Esimerkiksi, jos 4 ja 25 valitaan, kunkin päätekijöiden hajoamiset ovat vastaavasti 2² ja 5². Kuten voidaan nähdä, heillä ei ole mitään yleistä tekijää, joten 4 ja 25 ovat suhteellisia serkkuja.

Toisaalta, jos valitset 6 ja 24, kun teet niiden jakautumisen päätekijöistä, saadaan, että 6 = 2*3 ja 24 = 2³*3.

Kuten voidaan nähdä, näillä kahdella viimeisellä lausekkeella on ainakin yksi yleinen tekijä, siksi ne eivät ole suhteellisia serkkuja.

Suhteellisten serkkujen ominaisuudet

Yksityiskohta, jonka kanssa on oltava.

Toisaalta yllä oleva määritelmä voidaan tiivistää seuraavasti: Kaksi kokonaislukua “A” ja “B” ovat suhteellisia serkkuja, jos näiden suurin yhteinen jakaja on 1, ts. MCD (A, B ) = 1.

Tämän määritelmän kaksi välitöntä johtopäätöstä ovat:

-Jos "A" (tai "B") on ensisijainen luku, niin MCD (A, B) = 1.

-Jos "A" ja "B" ovat ensisijaisia ​​numeroita, niin MCD (A, B) = 1.

Toisin sanoen, jos ainakin yksi valituista numeroista on ensisijainen luku, niin lukupari on suhteelliset serkut.

Muut ominaisuudet

Muut tulokset, joita käytetään määrittämään, ovatko kaksi lukua suhteellisia serkkuja: ovat:

-Jos kaksi kokonaislukua ovat peräkkäisiä, niin nämä ovat suhteellisia serkkuja.

-Kaksi luonnollista lukua "A" ja "B" ovat suhteellisia serkkuja, jos ja vain jos numerot "(2^a) -1" ja "(2^b) -1" ovat suhteellisia serkkuja.

-Kaksi kokonaisluku "A" ja "B" ovat suhteellisia serkkuja, jos ja vain jos piirrettäessä piste (A, B) Cartesian tasoon ja rakenna alkuperän (0,0) ja (a , b), tämä ei sisällä mitään pistettä kokonaisilla koordinaateilla.

Esimerkit

1.- Harkitse kokonaisluku 5 ja 12. Molempien lukujen päätekijöiden hajoamiset ovat vastaavasti 5 ja 2²*3. Yhteenvetona voidaan todeta, että MCD (5,12) = 1, siksi 5 ja 12 ovat suhteellisia serkkuja.

2.- Anna numerot -4 ja 6. Sitten -4 = -2² ja 6 = 2*3, niin että MCD (-4,6) = 2 ≠ 1. Yhteenvetona -4 ja 6 eivät ole suhteellisia serkkuja.

Jos linja, joka kulkee tilattujen parien (-4,6) ja (0,0) läpi, ja mainitun viivan yhtälön määrittämiseksi voidaan varmistaa, että tämä kulkee pisteen läpi (-2,3).

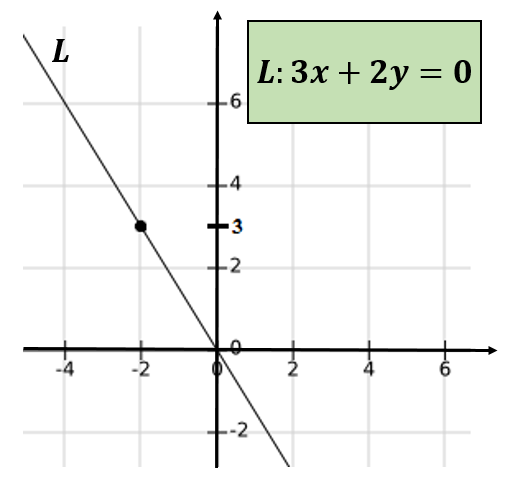
Jälleen on päätelty, että -4 ja 6 eivät ole suhteellisia serkkuja.

3.- Numerot 7 ja 44 ovat suhteellisia serkkuja ja ne voidaan päätellä nopeasti edellä sanottujen, koska 7 on ensisijainen luku.

4.- Harkitse numeroita 345 ja 346. Kaksi peräkkäistä lukua on varmistettu, että MCD (345 346) = 1, siksi 345 ja 346 ovat suhteellisia serkkuja.

5.- Jos otetaan huomioon numerot 147 ja 74, nämä ovat suhteellisia serkkuja, koska 147 = 3*7² ja 74 = 2*37, siksi MCD (147,74) = 1.

6.- Numerot 4 ja 9 ovat suhteellisia serkkuja. Osoittaaksesi sen voit käyttää edellä mainittua toista karakterisointia. Itse asiassa 2^4 -1 = 16-1 = 15 ja 2^9-1 = 512-1 = 511.

Saadut numerot ovat 15 ja 511. Näiden lukujen päätekijöiden hajoamiset ovat vastaavasti 3*5 ja 7*73, joten MCD (15 511) = 1.

Kuten näette, toisen karakterisoinnin käyttäminen on pidempi ja työlämpi työ sen tarkistamiseksi suoraan.

7.- Harkitse numeroita -22 ja -27. Sitten nämä numerot voidaan kirjoittaa uudelleen seuraavasti: -22 = -2*11 ja -27 = -3itin. Siksi MCD (-22, -27) = 1, niin -22 ja -27 ovat suhteellisia serkkuja.