Neliömäinen prisma

Selitämme, mikä on nelikulmainen prisma, sen ominaisuudet, kasvot, kärjet, reunat, kuinka laskea, esimerkit ja harjoitukset ratkaistaan

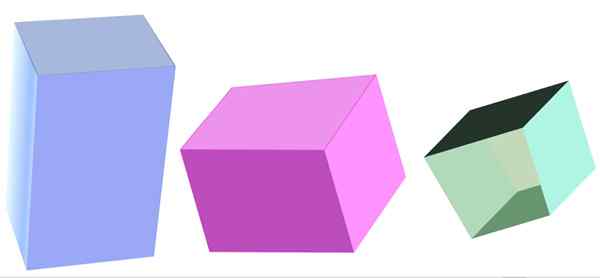
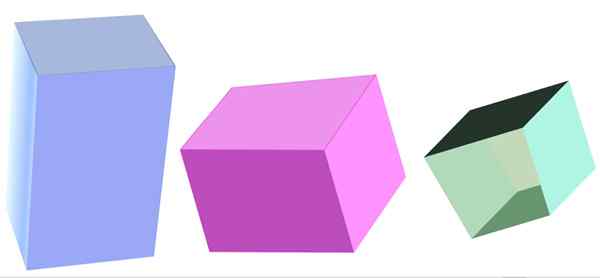Erityyppisiä kvadrangulaarisia prismia. Lähde: f. Zapata

Mikä on nelinkertainen prisma?

Hän Neliömäinen prisma Se on Polyhedros -perheen kolmiulotteinen geometrinen kuva. Se koostuu kahdesta yhtä suuresta ja yhdensuuntaisesta pinnasta, jonka muodossa on kvadrilateraalinen, ja sivuilla neljä rinnakkaisgrammia.

Niiden luokitteluun on useita kriteerejä, koska kasvojen ja kaltevuuden muotoon on monia mahdollisuuksia. Esimerkiksi on Suora kotijuoksut prismat ja kaltevat kvadrangulaariset prismat.

Ensimmäisessä tapauksessa sivut ovat kohtisuorassa pohjaan nähden, ja sitten ne ovat suorakulmioita tai neliöitä. Toisessa tapauksessa sivupinnat ovat kaltevia pohjaan nähden, siksi ne eivät voi olla suorakulmioita tai neliöitä.

Lisäksi kvadrangulaarinen prisma voi olla säännöllistä tai epäsäännöllistä, pohjasta riippuen on säännöllinen tai epäsäännöllinen nelikulmainen. Tavallinen nelikulmainen on neliö, jonka neljä sivua ja sen neljä kulmaa mittaavat saman .

Esimerkki erityisestä kotikäyttöprismista on rinnakkaispiped, jonka emäkset ovat rinnakkaisia. Laatikoiden ja tiilien muodot ovat inspiraatiota nelinkertaisista prismista, joten hyviä esimerkkejä tämän geometrisen hahmon käytöstä käytännöllisissä sovelluksissa ovat.

Neljänneksen prisman ominaisuudet

Neljänneksen prisman tärkeimmistä ominaisuuksista ovat seuraavat:

• Heidän kasvonsa on monikulmio.
• Siinä on yhteensä 6 pintaa (2 emäksiä ja 4 puolta), 12 reunaa tai reunaa ja 8 kärkeä (kulmaa).
• Sivupinnat voidaan muotoilla kuten: neliö, suorakulmio, rinnakkainen ohjelma, rhombus tai rhomboidi.
• Sen sivut voivat olla suorat (muoto 90º emäksillä) tai kallistettu (sisäpuolella on kulma alle 90º).
• Suorien prismien sivuttaiset kasvot voivat olla vain neliöitä tai suorakulmioita.
• Myös prisman perustat saavat nimen ohjeet.
• Jos pohja on säännöllinen kvadrilateraalinen, myös nelikulmainen prisma on säännöllinen. Koska tasainen luku on säännöllinen, jos kaikilla sen sivuilla on sama mitta, ainoa mahdollisuus on, että emäkset ovat neliöitä.
• Kun prisman perusta on mikä tahansa muu nelikulmainen, erilainen kuin neliö, niin prismaa pidetään epäsäännöllisenä.
• Säännöllinen nelikulmainen prisma voidaan rekisteröidä sylinteriin.

Voi palvella sinua: Päätelmätilastot: Historia, ominaisuudet, mitä se on, esimerkkejä

Nelikulmaisen prisman elementit

Neljänneksen prisman viisi elementtiä ovat yhteisiä kaikille prismille:

• Pohjat, muodostettu kahdella identtisellä ja rinnakkaisella neljänneksellä.
• Sivuttaiset kasvot, ovat neljä rinnakkaisgrammia, jotka rajoittavat lukua.
• Kärjet tai kulmat, yleiset kohdat, joilla on prisman kolme vierekkäistä puolta.
• Reunat tai reunat, yhteinen segmentti, jolla on kaksi vierekkäistä kasvot.
• Korkeus: Se on kohtisuoran segmentin pituus, jonka päät ovat emäkset. Kun prisma on suora, korkeus osuu sivusuuntaisten reunojen mittaan.
• Suorakulmio, Prisman ja tason välinen risteysalue, joka muodostaa 90º sivureunojen kanssa.

Seuraava kuva näyttää jokaisen näiden elementtien suoran nelikulmaisen prisman:

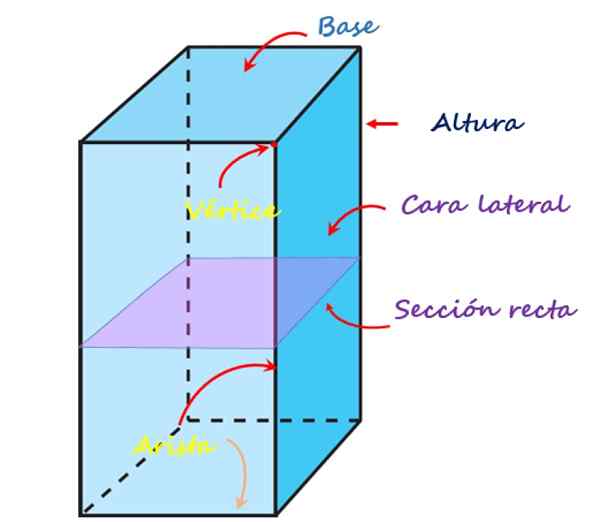Nelikulmaisen prisman elementit. Lähde: f. Zapata

Kasvot, kärjet ja reunat

Neljänneksen prisman tutkiminen ovat erittäin tärkeitä kasvot, kärkipisteet ja reunat:

Kasvot

Prisman kasvot tekevät yhteensä 6: 2 identtistä emäksiä nelinkertaisen muodossa ja 4 sivuta tai kasvot rinnakkaisohjelman muodossa.

Kärjet

Ne ovat kuvan kulmia, kohta, jossa kolme vierekkäistä kasvot tulevat.

Reunat

Ne ovat prisman kasvojen risteyssegmenttejä. Reunat luokitellaan seuraavasti:

• Perusreunat, Yleiset segmentit emäksen ja sivupintojen välillä.
• Sivureunat, Kuten nimestä voi päätellä, ne ovat yleisiä segmenttejä sivupintojen keskuudessa.

Yläkuvio näyttää kaksi tyyppiä reunoja, jotka on nimetty eri värillisillä nuolilla. Reunojen lukumäärä n_-Lla voidaan määrittää Euler -lause polyhedrosista, joka liittyy reunojen lukumäärään kasvojen n_C ja kärkipisteet n_V-

Voi palvella sinua: matemaattiset toiminnot

N_-Lla = N_C + N_V −2

Neljänneksen prisma n_C = 6 ja n_V = 8, siksi:

N_-Lla = 6 + 8 −2 = 12

Siksi nelikulmaisen prisman reunojen tai reunojen lukumäärä on 12.

Kuinka laskea nelikulmaisen prisman tilavuus?

Prisman tilavuus ymmärretään sen lukittuna avaruuden osana, ja se mitataan kuutioyksiköinä, jotka voivat olla kuutiometriä, kuutiometriä, kuutiometriä tai muuta sopivaa, edellyttäen, että ne ovat kuution pituisia.

Osa V on aina positiivinen määrä, ja minkä tahansa kvadrangularisen prisman tapauksessa se antaa tuotteen pohjan välillä_{b -} ja korkeus H:

V = a_{b -} × H

Yo) Säännöllinen nelikulmainen prisman tilavuus

Koska tukikohdat ovat neliömäisiä ja neliön neliö on sen sivu ℓ neliö:

-Lla_{b -} = ℓ²

Sitten prisman tilavuus, jonka korkeus on "H", on:

V = ℓ² × H

Ii) Epäsäännöllinen nelikulmainen prisman tilavuus

Se riippuu prisman pohjan muodosta ja korkeudesta H ":

1.- Suorakaiteen muotoinen prisma

Sivujen alue suorakulmion "A" ja "B" on:

-Lla_{b -} = A × B

Joten tilavuus on:

V = a × b × H

2.- Romboidaalinen perusprisma

Rhombus -alue on ”D” ja “D” diagonaaliensa osittain tuote:

Ja tilavuus on:

3.- Romboid -muotoinen perusprisma

Rhomboidi -muotoinen pohjaalue on sen pohjan "B" ja sen suhteellisen korkeuden H -tuote_{r -}”Tähän pohjaan, joka on kohtisuora segmentti, joka siirtyy tästä pohjasta sen rinnakkaispuolelle.

-Lla_{b -} = B × H_{r -}

Siksi prisman tilavuus tällä pohjalla on:

Voi palvella sinua: mikä on tilastoalue? (Esimerkkejä)

V = B × H_{r -} × H

4.- Trapetsoidinen perusprisma

Koska trapezoidin pinta -ala on rinnakkaisten sivujen "A" ja "B" puoliväli, kerrottuna sen korkeudella "C":

Trapetsoidisen prisman tilavuus on:

5.- Trapetsoidi -muotoinen perusprisma

Symmetrisen trapetsoidin pinta -ala on sen diagonaalien D ja D puolitetuote, siksi:

Tässä tapauksessa prisman tilavuus on:

Liikuntaa

Trapetsoidisen emäksen nelikulmaisen prisman tilavuus on 648 cm³. Trapetsoidimitta a = 10 cm ja b = 5 cm, kun taas trapetsin korkeus on c = 6 cm. Näiden tietojen kanssa löydä prisman korkeus.

Ratkaisu

Koska pohjan mitat ovat, alueesi voidaan helposti laskea:

Ja kaava:

V = a_{b -} × H

”H” puhdistetaan, prisman korkeus, koska sen tilavuus on tiedossa:

H = v/ a_{b -} = 648 cm³ / 45 cm² = 14.4 cm

Esimerkit

Suorakulmainen prisma tai kuutio

Tämän suoran prisman kuusi kasvot ovat neliömäisiä tai suorakaiteen muotoisia. Laatikot ovat esimerkkejä suorakulmaisista prismoista, muodosta, jota käytetään myös lukuisissa esineissä ja rakenteissa, kuten rakennuksissa.

Kuutio

Kuutio on tavallinen nelikulmainen prisma, jonka kuusi sivua on muotoiltu neliönä, esimerkiksi noppaa tai hyvin tunnettu Rubikin kuutiopeli.

Kuutio on osa platoonisten kiinteiden aineiden ryhmää, geometrisia lukuja, jotka täyttävät kaksi ehtoa. Ensimmäinen on, että jokainen kasvo on tavallinen monikulmio ja toinen on, että jokaisella kärkipisteellä on yhteinen sama määrä kasvoja.

Kuutio täyttää molemmat ehdot, koska niiden kasvot ovat neliömuoto, joka on tavallinen monikulmio. Ja jokaisessa kuution kahdeksassa kärkipisteessä saman konvergon kolme kasvot.

Jäljellä olevat platoniset kiinteät aineet ovat tetraedri, oktaedri, dodekaedro ja icosaedro.