Poliittisen prosessin ominaisuudet, sovellukset ja esimerkit

Eräs Poliittinen prosessi Se on termodynaaminen prosessi, joka tapahtuu, kun paineen välinen suhde P ja tilavuus V antama P.Vⁿ Se pysyy vakiona. Eksponentti n Se on todellinen luku, yleensä nollan ja äärettömyyden välillä, mutta joissakin tapauksissa voi olla negatiivinen.

Arvo n saada nimi Poliittinen indeksi Ja on tärkeää korostaa, että polytrooppisen termodynaamisen prosessin aikana indeksin on ylläpidettävä kiinteää arvoa, muuten prosessia ei pidetä polytrooppisena.

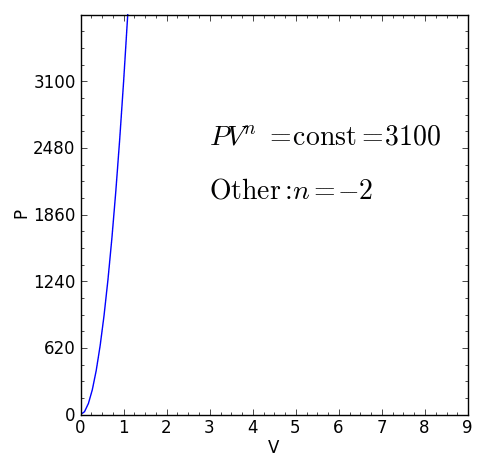
Kuvio 1. Polytrooppisen termodynaamisen prosessin ominaisyhtälö. Lähde: f. Zapata.

[TOC]

Polytrooppisten prosessien ominaisuudet

Joitakin polytrooppisten prosessien ominaisia ​​tapauksia ovat: 

- Isoterminen prosessi (vakiona t -lämpötilassa), jossa eksponentti on n = 1.

- Isobarinen prosessi (vakiopaine P), tässä tapauksessa n = 0.

- Isocoric -prosessi (tilavuus V vakiona), jolle n =+∞.

- Adiabaattiset prosessit (vakio entropia), joissa eksponentti on n = γ, koska γ adiabaattinen vakio. Tämä vakio on osoitus lämpökapasiteetin välillä vakiopaine CP: ssä jaettuna lämpökapasiteettilla vakiona CV -tilavuudella:

γ = CP/CV

- Mikä tahansa muu termodynaaminen prosessi, joka ei ole mikään aikaisemmista tapauksista. Mutta noudattaa P.Vⁿ = CTTE Oikealla ja vakiona poltropisella indeksillä n Se on myös polytropinen prosessi.

Kuva 2. Polytropisten termodynaamisten prosessien erilaiset ominaispiirteet. Lähde: Wikimedia Commons.

Sovellukset

Yksi polytrooppisen yhtälön tärkeimmistä sovelluksista on suljetun termodynaamisen järjestelmän tekemän työn laskeminen, kun se siirtyy alkuperäisestä tilasta toiseen päättymään lähes kvasi -astaattisella tavalla, ts. Tasapainotilojen peräkkäisyyden jälkeen.

Työskentele polytrooppisissa prosesseissa N: n eri arvoihin

N ≠ 1: lle

Suljetun termodynaamisen järjestelmän suorittama mekaaninen työ lasketaan ekspressiolla:

W = ∫p.DV

Voi palvella sinua: Diamagnetismi: Materiaalit, sovellukset, esimerkit

Missä p on paine ja V tilavuus.

Kuten polytrooppisen prosessin tapauksessa, paineen ja tilavuuden välinen suhde on:

P.V ⁿ = vakio = c

Edellisen lausekkeen puhdistaminen sen korvaamiseksi työn ilmaisussa:

P = c /V ⁿ

Sinulla on mekaaninen työ tehty polytropisen prosessin aikana, joka alkaa alkuperäisessä tilassa 1 ja päättyy lopulliseen tilaan 2. Kaikki tämä näkyy seuraavassa lausekkeessa:

Jos n ≠ 1, niin sinulla on:

Lisäksi, koska alkuperäiset ja lopulliset tilat on määritelty hyvin, niin vakio määritetään myös seuraavalla lausekkeella:

C = p₁ V₁ⁿ = P₂ V₂ⁿ

Korvaamalla vakion arvo työn ilmaisussa saadaan:

W = (p₂ V₂ - P₁ V₁)/(1-N)

Jos työainetta voidaan mallintaa ihanteellisena kaasuna, seuraava tilayhtälö on:

P.V = m.R -.T

Missä m on ihanteellisen kaasun moolien lukumäärä ja r on kaasujen yleinen vakio.

Ihanteelliselle kaasulle, joka seuraa polytrooppista prosessia, jonka polytropiaindeksi on erilainen kuin yksikkö ja joka kulkee tilasta, jolla on alkulämpötila T₁ toiseen tilaan lämpötilan t kanssa₂ Tehty työ saadaan seuraavalla kaavalla:

W = m r (t₂ - T₁)/(1-N)

N → ∞

Edellisessä osassa saadun työn kaavan mukaan polytrooppisen prosessin työ n = ∞: lla on nolla, koska työn ilmentyminen on jaettu äärettömyyden välillä ja siksi tuloksella on taipumus nolla.

Toinen tapa saavuttaa tämä tulos on aloittaa P -suhteesta₁ V₁ⁿ = P₂ V₂ⁿ, joka voidaan kirjoittaa uudelleen seuraavasti:

(P₁/P₂) = (V₂/V1)ⁿ

N-pakseton juuren ottaminen jokaisessa jäsenessä, jonka saat:

(V₂/V1) = (P₁/P₂-A^(1/N)

Jos n → ∞, sinun on (v₂/V1) = 1, mikä tarkoittaa sitä:

Voi palvella sinua: Ceded Heat: Formulat, miten se lasketaan ja ratkaistaan ​​harjoituksia

V₂ = V₁

Toisin sanoen tilavuus ei muutu polytrooppisessa prosessissa n → ∞: n kanssa. Siksi DV -tilavuuserot mekaanisen työn integraalissa on 0. Tämäntyyppiset polytrooppiset prosessit tunnetaan myös prosesseina isocorinen, o Prosessit vakiotilavuudella.

N = 1

Jälleen meillä on ilmaus työhön:

W = ∫p DV

Polytrooppisen prosessin tapauksessa n = 1 paineen ja tilavuuden välinen suhde on:

P v = vakio = c

Selvittämällä edellisen lausekkeen ja korvaamisen P, sinulla on tehty työ siirtyäksesi alkuperäisestä tilasta 1 lopulliseen tilaan 2:

W = ∫12P DV = CTTE ∫12 V^( - 1) DV = CTTE (ln (V2) - ln (V1))

Tarkoittaen:

W = c ln (v₂/V₁-A.

Koska alkuperäiset ja lopulliset tilat ovat hyvin määritettyjä, samoin CTTE. Tarkoittaen:

C = p₁ V₁ = P₂ V₂

Lopuksi, seuraavat hyödylliset lausekkeet ovat käytettävissä polyitrooppisen suljetun järjestelmän mekaanisen työn löytämiseksi, jossa n = 1.

W = p₁ V₁ ln (v₂/V₁) = P₂ V₂ ln (v₂/V₁-A

Jos työaine koostuu m Ihanteellisen kaasun moolit, sitten ihanteellinen kaasuyhtälö voidaan käyttää: p v = m.R -.T.

Tässä tapauksessa, kuten p.V₁ = CTTE, polytrooppinen prosessi, jossa on n = 1, on prosessi vakio -T -lämpötilassa (isoterminen), jotta saadaan seuraavat lausekkeet:

W = m r t₁ ln (v₂/V₁) = m r t₂ ln (v₂/V₁-A

Kuva 3. Carambanin sulaminen, esimerkki isotermisen prosessista. Lähde: Pixabay.

Esimerkkejä polytrooppisista prosesseista

- Esimerkki 1

Oletetaan sylinteri, jossa siirrettävä mäntä on täynnä kiloa ilmaa. Aluksi ilmalla on tilavuus V₁= 0,2 m³ Paineessa p₁= 400 kPa. Polytrooppista prosessia seurataan n = γ = 1,4, jonka lopullisella tilalla on paine P₂ = 100 kPa. Määritä männän ilman tekemä työ.

Ratkaisu

Kun polytropiaindeksi on yhtä suuri kuin adiabaattinen vakio, on olemassa prosessi, jossa työaine (ilma) ei vaihda lämpöä ympäristön kanssa, ja siksi se ei muuta entropiaa.

Se voi palvella: Kolmas termodynamiikan laki: kaavat, yhtälöt, esimerkit

Ilmalle, ihanteelliselle diatomiselle kaasulle, sinulla on:

γ = CP/CV, CP = (7/2) R ja CV = (5/2) r

Niin:

γ = 7/5 = 1,4

Käyttämällä polytrooppisen prosessin ilmentymistä ilman lopullinen tilavuus voidaan määrittää:

V₂ = [P₂ V₁^1.4)/P₂-^(1/1,4) = 0,54 m³.

Nyt on olemassa olosuhteet, joilla sovelletaan edellä saatu N ≠ 1: n polytrooppisessa prosessissa tehdyn työkaavan soveltaminen:

W = (p₂ V₂ - P1 V1)/(1-N)

Asianmukaisten arvojen korvaaminen on:

W = (100 kPa 0,54 m³ - 400 kPa 0,2 m³)/(1 - 1,4) = 65,4 kJ

- Esimerkki 2

Oletetaan sama esimerkin 1 sylinteri, kun siirrettävä mäntä on täynnä kiloa ilmaa. Aluksi ilmalla on tilavuus V1 = 0,2 m³ Paineessa P1 = 400 kPa. Mutta toisin kuin edellinen tapaus, ilma laajenee isotermisesti saavuttaakseen lopullisen paine P2 = 100 kPa. Määritä männän ilman tekemä työ.

Ratkaisu

Kuten aiemmin nähtiin, isotermiset prosessit ovat polytrooppisia prosesseja, joissa on indeksi n = 1, joten on toteutettu, että:

P1 V1 = P2 V2

Tällä tavoin lopullinen tilavuus voidaan helposti irrottaa:

V2 = 0,8 m³

Sitten käyttämällä tapausta n = 1 aikaisemmin saadun työn ilmaisua, sinun on työskenneltävä männän ilmassa tässä prosessissa: on:

W = P1 V1 Ln (V2/V1) = 400000 Pa × 0,2 m³ ln (0,8/0,2) = 110,9 kJ.  

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Cengel, ja. 2012. Termodynamiikka. 7. painos. McGraw Hill.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Nesteet ja termodynamiikka. Toimittanut Douglas Figueroa (USB).
4. López, c. Termodynamiikan ensimmäinen laki. Toipunut: Culturacientifica.com.
5. Ritari, r. 2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
6. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9na ed. Cengage -oppiminen.
7. Sevillan yliopisto. Lämpökoneet. Toipunut: Laplace.meille.On.
8. Wikiwand. Poliittinen prosessi. Toipunut: Wikiwand.com.