Dynaamiset ohjelmointiominaisuudet, esimerkki, edut, haitat

Se Dynaaminen ohjelmointi Se on algoritmimalli, joka ratkaisee monimutkaisen ongelman jakamalla sen alihankoihin, tallentamalla niiden tulokset välttääksesi näiden tulosten laskemista.

Tätä ohjelmaa käytetään, kun ongelmat voidaan jakaa samanlaisiksi alakerroksiksi, jotta niiden tuloksia voidaan käyttää uudelleen. Suurin osa enemmistöstä tätä ohjelmaa käytetään optimointiin.

Dynaaminen ohjelmointi. Fibonacci -peräkkäin päällekkäiset alaproblemit. Lähde: Wikimedia Commons, AT: Käyttäjä: Dcoatzee, käyttäjän jäljitetty: Standered / Public Domain

Ennen käytettävissä olevan alaprobleman ratkaisemista dynaaminen algoritmi yrittää tutkia aiemmin ratkaistujen alaryhmien tuloksia. Alasopimusratkaisut yhdistetään parhaan ratkaisun saavuttamiseksi.

Sen sijaan, että laskettaisiin sama alaproblema uudestaan ​​ja uudestaan, ratkaisusi voidaan tallentaa johonkin muistiin, kun täytät tämän alaprobleman ensin. Kun se ilmestyy jälleen toisen alaryhmän ratkaisun aikana, otetaan jo tallennettu ratkaisu.

Tämä on hieno idea korjata aikaa muistilla, missä lisätilaa käytettäessä voit parantaa ratkaisun löytämiseen tarvittavaa aikaa.

[TOC]

Dynaamisen ohjelmoinnin ominaisuudet

Seuraavat olennaiset ominaisuudet ovat ne, joita ongelmaa voidaan soveltaa dynaamiseen ohjelmointiin:

Optimaalinen alarakenne

Tämä ominaisuus ilmaisee, että optimointiongelma voidaan ratkaista yhdistämällä toissijaisten ongelmien optimaaliset ratkaisut, jotka tekevät siitä. Nämä optimaaliset alirakenteet kuvataan rekursiona.

Esimerkiksi kaaviossa optimaalinen alarakenne esitetään lyhyimmässä reitillä, joka kulkee kärkipisteestä kärkeen t:

Eli tällä lyhyimmässä reitillä R voit käyttää mitä tahansa välivaunua I. Jos R on todella lyhin reitti, niin se voidaan jakaa Subrutas R1: hen (S: stä I: stä) ja R2: sta (I: stä T: hen), niin että nämä ovat puolestaan ​​lyhyimpiä reittejä vastaavien kärkipisteiden välillä.

Siksi lyhimpien reittien löytämiseksi voit helposti muotoilla ratkaisun rekursiivisesti, mitä Floyd-Warshall-algoritmi tekee.

Päällekkäiset alakerrokset

Alavirheiden on oltava pieni. Toisin sanoen minkä tahansa ongelman ratkaiseva rekursiivinen algoritmi on ratkaistava samat aliohjelmat uudestaan ​​ja uudestaan ​​sen sijaan.

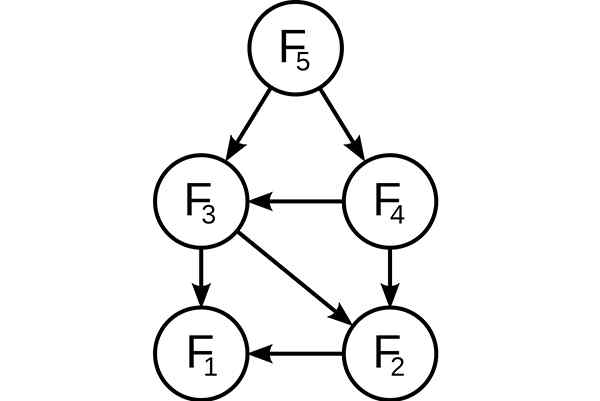
Esimerkiksi Fibonacci-sarjan luomiseksi tämä rekursiivinen formulaatio voidaan harkita: FN = F (N-1) + F (N-2), ottaen perustapauksena, että F1 = F2 = 1. Sitten sinun täytyy: f33 = f32 + f31 ja f32 = f31 + f30.

Kuten voidaan nähdä, F31 ratkaistaan ​​sekä F33: n että F32: n rekursiivisissa ala -alueilla. Vaikka alihankojen kokonaismäärä on todella pieni, jos rekursiivinen ratkaisu otetaan käyttöön, koska se lopulta ratkaisee samat ongelmat uudestaan ​​ja uudestaan.

Voi palvella sinua: tietojärjestelmän 7 komponenttia

Tämä otetaan huomioon dynaamisella ohjelmoinnilla, joten se ratkaisee jokaisen alaproblemin vain kerran. Tämä voidaan saavuttaa kahdella tavalla:

Ylin lähestymistapa

Jos ratkaisu mihin tahansa ongelmaan voidaan formuloida rekursiivisesti niiden alakohteiden ratkaisun avulla, ja jos nämä alihankojen päällekkäisyydet ovat päällekkäisiä, alaryhmien ratkaisut voidaan helposti muistaa tai tallentaa taulukon taulukkoon.

Joka kerta kun etsitään uuden alaprobleman ratkaisua, sitä tarkistetaan taulukossa, jos aiemmin on ratkaistu. Jos ratkaisu tallennetaan, sitä käytetään sen sijaan, että laskisivat sen uudelleen. Muutoin alproblema ratkaistaan, ja tallentaa liuos taulukkoon.

Nouseva lähestymistapa

Kun ongelman ratkaisu on formuloitu rekursiivisesti sen alihankojen suhteen, ongelma voidaan kokeilla ylöspäin: ensin he yrittävät ratkaista alihankot ja käyttää ratkaisujaan ratkaisujen saavuttamiseen suurimpiin alihankoihin.

Tämä tehdään yleensä myös taulukon muodossa, tuottaen iteratiivisia ratkaisuja yhä suuremmille alihankoihin käyttämällä ratkaisuja pieniin alihankoihin. Esimerkiksi, jos F31: n ja F30: n arvot tunnetaan jo, F32: n arvo voidaan laskea suoraan.

Vertailu muihin tekniikoihin

Merkittävä kuuluu ongelmaan, joka voidaan ratkaista dynaamisella ohjelmoinnilla. Tämä erottaa jakautumisen ja valloittamisen tekniikan dynaamisen ohjelmoinnin, missä yksinkertaisimpia arvoja ei ole välttämätöntä.

Se on samanlainen kuin rekursio, koska laskemalla emätapaukset lopullinen arvo voidaan määrittää induktiivisesti. Tämä nouseva lähestymistapa toimii hyvin, kun uusi arvo riippuu vain aikaisemmin laskettuista arvoista.

Esimerkki

Vähimmäisvaiheet saavuttaaksesi 1

Jokaiselle positiiviselle kokonaisluku ”E” voit suorittaa minkä tahansa seuraavista kolmesta vaiheesta.

- Vähennä 1 numerosta. (E = E-1).

- Jos se on jaettavissa 2: lla, se jaetaan 2: lla (jos E%2 == 0, niin e = e/2).

- Jos se on jaettavissa 3: lla, se jaetaan 3: lla (jos E%3 == 0, niin e = e/3).

Edellisten vaiheiden perusteella sinun on löydettävä vähimmäismäärä näitä vaiheita ja 1. Esimerkiksi:

- Jos E = 1, tulos: 0.

- Jos E = 4, tulos: 2 (4/2 = 2/2 = 1).

- Kun E = 7, tulos: 3 (7-1 = 6/3 = 2/2 = 1).

Lähestyä

Saatat aina ajatella askeleen valitsemista, joka tekee n mahdollisimman alhaisesta ja jatkaa näin, kunnes se saavuttaa 1. Voidaan kuitenkin nähdä, että tämä strategia ei toimi täällä.

Voi palvella sinua: Kaupallinen ohjelmisto

Esimerkiksi, jos E = 10, vaiheet olisivat: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 vaihetta). Optimaalinen tapa on kuitenkin: 10-1 = 9/3 = 3/3 = 1 (3 vaihetta). Siksi kaikki mahdolliset vaiheet, jotka voidaan suorittaa jokaiselle N: n arvolle, on todistettava, valitsemalla näiden mahdollisuuksien vähimmäismäärä.

Kaikki alkaa rekursiosta: f (e) = 1 + min f (e-1), f (e/2), f (e/3), jos e> 1, kantapaikkana ottaminen: f (1 ) = 0. Toistumisyhtälöllä voit aloittaa rekursion koodaamisen.

Voidaan kuitenkin havaita, että se on päällekkäin alaproblemit. Lisäksi tietylle tulolle optimaalinen ratkaisu riippuu alaryhmien optimaalisesta ratkaisusta.

Kuten muistamisessa. Tai kuten dynaamisessa ohjelmoinnissa, se alkaa alhaalta, etenee annetulle E. Seuraavaksi molemmat koodit:

Muistaminen

Dynaaminen ylöspäin suuntautuva ohjelmointi

Edut

Yksi dynaamisen ohjelmoinnin käytön tärkeimmistä eduista on, että se kiihdyttää prosessointia, koska aiemmin laskettuja viitteitä käytetään. Kuten rekursiivinen ohjelmointitekniikka, se vähentää ohjelmakoodirivit.

Vorace Algoritmos vs Dynaaminen ohjelmointi

Ryhmättömät algoritmit ovat samanlaisia ​​kuin dynaaminen ohjelmointi siinä mielessä, että molemmat ovat optimointia työkaluja. Voraz -algoritmi etsii kuitenkin optimaalista ratkaisua jokaisessa paikallisessa vaiheessa. Eli se etsii ahneutta valintaa toivoen löytää globaali optimaalinen.

Siksi turvattomat algoritmit voivat tehdä oletuksen, joka näyttää tuolloin optimaalisesti, mutta siitä tulee tulevaisuudessa kallista eikä takaa globaalia optimaalista.

Toisaalta dynaaminen ohjelmointi löytää optimaalisen ratkaisun alihankoihin ja tekee sitten tietoisen valinnan yhdistämällä näiden alihankojen tulokset todella löytääkseen optimaalisen ratkaisun,.

Haitat

- Kunkin alihankkeen lasketun tuloksen tallentamiseksi tarvitaan paljon muistia, jotta voitaisiin varmistaa, että tallennettua arvoa käytetään tai ei.

- Monta kertaa lähtöarvo tallennetaan ilman,. Tämä johtaa muistin tarpeettomaan käyttöön.

- Dynaamisessa ohjelmoinnissa toimintoja kutsutaan rekursiivisesti. Tämä saa akun muistin pysymään jatkuvassa lisäyksessä.

Rekursiivisuus vs. dynaaminen ohjelmointi

Jos sinulla on rajoitettu muisti koodin suorittamiseksi ja prosessointinopeus ei ole huolestuttava, voidaan käyttää rekursiivisuutta. Esimerkiksi, jos mobiilisovellusta kehitetään, muisti on hyvin rajoitettu sovelluksen suorittamiseen.

Voi palvella sinua: Sekoitukset: Ominaisuudet ja esimerkit

Jos ohjelman halutaan suoritettavan nopeammin ja muistirajoituksia ei ole, on parempi käyttää dynaamista ohjelmointia.

Sovellukset

Dynaaminen ohjelmointi on tehokas menetelmä ongelmien ratkaisemiseksi, jotka muuten voisivat tuntua erittäin vaikealta ratkaista kohtuullisessa ajassa.

Dynaamiseen ohjelmointiparadigmaan perustuvia algoritmeja käytetään monilla tiedealueilla, mukaan lukien monia esimerkkejä keinotekoisessa älykkyydessä, suunnitteluongelmien ratkaisemisesta äänentunnistukseen.

Dynaamiset ohjelmointialgoritmit

Dynaaminen ohjelmointi on melko tehokasta ja palvelee erittäin hyvin monenlaisia ​​ongelmia. Monia algoritmeja voidaan nähdä vääriä algoritmeja, kuten:

- Fibonacci -numerosarja.

- Hanoi -tornit.

- Floyd-Warshallin kaikki lyhyimmät reitit parit.

- Reppu.

- Projektin ohjelmointi.

- Dijkstra: n lyhin polku.

- Robotiikan lennonhallinta ja hallinta.

- Matemaattiset optimointiongelmat.

- Jaettu aika: Ohjelma työ suorittimen käytön maksimoimiseksi.

Fibonacci -numerosarja

Fibonacci -numerot ovat seuraavassa järjestyksessä löydetyt numerot: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144 jne.

Matemaattisessa terminologiassa FIBONACCI -lukujen FN -peräkkäisyys määritetään toistumiskaavalla: f (n) = f (n -1) + f (n -2), missä f (0) = 0 ja f (1) = 1.

Ylin lähestymistapa

Tässä esimerkissä hakumatriisi, jolla on kaikki alkuperäiset arvot, alustetaan -1: llä. Aina kun ratkaisu alasäätimeen tarvitaan, sitä etsitään ensin tässä hakumatriisissa.

Jos laskettu arvo on, tämä arvo palautetaan. Muutoin tulos lasketaan sen tallentamiseksi hakumatriisiin ja siten kykenevä käyttämään sitä myöhemmin.

Nouseva lähestymistapa

Tässä tapauksessa samalle Fibonacci -sarjalle F (0), sitten F (1), F (2), F (3) ja niin edelleen lasketaan ensin. Siten pohjan alaryhmien ratkaisut rakennetaan.

Viitteet

1. Viinet Choudhary (2020). Johdatus dynaamiseen ohjelmoinniin. Kehittimen sisäpiiriläinen.Otettu: Kehittäjä.yhteistyö.
2. Alex Allain (2020). Dynaaminen ohjelmointi C: ssä++. C -ohjelmointi. Otettu: cprogrammming.com.
3. Akatemian jälkeen (2020). Idea dynaamisesta ohjelmoinnista. Otettu: Afteracademy.com.
4. Aniruddha Chaudhari (2019). Dynaaminen ohjelmointi ja rekursio | Eri. CSE -pino. Otettu: CSESTACK.org.
5. Koodikokki (2020). Dynaamiseen ohjelmointi -opetusohjelmaan. Otettu: Codhef.com.
6. Ohjelma (2020). Dynaaminen ohjelmointi. Otettu: Ohjelma.com.