Kotisivu
Matematiikka
Rajoita ominaisuuksia (esimerkkien kanssa)

Matematiikka

Rajoita ominaisuuksia (esimerkkien kanssa)

Se Rajoittaa ominaisuuksia Ne ovat joukko algebrallisia sääntöjä ja menettelyjä, joita käytetään niiden määrittämiseen. Rajakonsepti on välttämätön laskennassa ja sen arvon löytämisessä ei tarvitse olla monimutkainen tehtävä, edellyttäen, että sen ominaisuuksia käsitellään helposti.

Alla on luettelo tärkeimmistä, ja siihen liittyy sovellusesimerkkejä.

Rajat ja sen ominaisuudet ovat laskelman perusta. Hyvin erityinen raja on esitetty kuvassa: f (x) -funktion johdannainen

Olkoon b, c, n, a ja b reaalilukuja ja F ja g Tällaiset toiminnot, jotka tarkistavat seuraavat:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Sitten sinulla on seuraavat ominaisuudet:

1. Suoran vaihtoraja

Ensinnäkin funktion f raja, kun x → c voidaan laskea suoraan korvaamalla x = c funktiossa. Jos funktio on x = c, raja on:

$\lim_x \rightarrow c f(x)=f(c)$ Mutta ei välttämättä funktio on määriteltävä x = C: ssä, jotta raja on olemassa. Ajatuksena on lähestyä niin paljon kuin haluat X = C: n arvoa ja nähdä, mitä funktion kanssa tapahtuu siinä tapauksessa.

Esimerkki

Löydä F (x) = x -raja² Kun x → 4

Ratkaisu

Raja ratkaisee yksinkertaisesti korvaamalla x = 4 f (x) = x: ssä², Koska operaation suorittamisessa ei ole haittaa:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Rajan ainutlaatuisuus

Jos funktion F (x) raja, kun x → c on olemassa ja se on L: n arvoinen, sanoi raja on ainutlaatuinen.

Siksi sivurajat, jotka ovat ne, kun x → c^- (Lue ”X: llä on taipumus c vasemmalta”) ja kun x → c⁺(Se lukee ”X: llä on taipumus c oikealla”), molemmat ovat olemassa ja sillä on sama arvo l, vaikka toimintoa ei määritetä x = c.

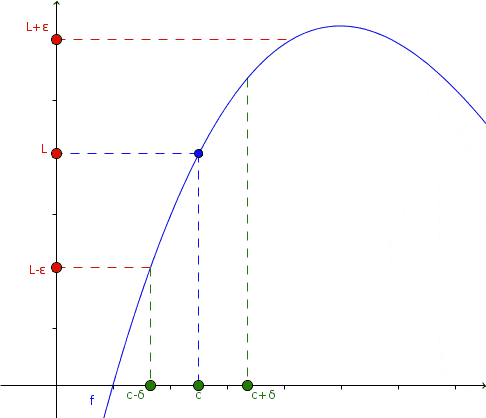Tässä animaatiossa esitetään rajan käsite: Kun X pyrkii tiettyyn arvoon C, lähestyen sekä vasemmalla että oikealla, funktion arvo on yleensä l. Ei välttämättä funktio määritetään x = c. Lähde: Wikimedia Commons.

Animaatiossa tätä lähestymistapaa havaitaan ja mitä funktion kanssa tapahtuu siinä tapauksessa: onko se lähestymässä vasemmalla ja oikealla x = c, funktion arvo puolestaan on lähellä L.

Voi palvella sinua: vähimmäisruutuja

Matemaattisesti ilmaisee tällä tavalla:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Sivusuuntaiset rajat sallivat tietää, milloin raja on olemassa tai ei, koska jos niitä ei ole tai jos ne eroavat toisistaan, on varmaa, että funktion raja, kun x → c ei ole.

Esimerkki

Laske F (x) -raja, kun x → 1, jos se on olemassa, missä f (x) annetaan:

Ratkaisu

Tämä on osien funktio tai määritelty kappaleiksi, joka koostuu linjan 4 -X: stä x: n arvoille < 1 y en la parábola 4 - x² Kun x on yhtä suuri kuin yksi tai suurempi kuin 1.

Voimme lähestyä x = 1 vasemmalta, tässä tapauksessa x: lle pätevä funktion osa otetaan<1:

Koska sivuttaisrajat ovat samat, seuraa, että funktion raja, kun x → 1 on olemassa ja on 3 arvoinen.

3. Vakio

Vakion raja on mainitun vakion arvo riippumatta siitä, mistä muuttujalla on taipumus:

$\lim_x\rightarrow cb=b .$

Esimerkki

Laskea:

$\lim_x\rightarrow 1\pi$ Ratkaisu

$\lim_x\rightarrow 1\pi= \pi$

4. Identiteettifunktioraja

Jos f (x) = x, se on aina toteutunut:

$\lim_x\rightarrow cx=c$

Esimerkki

Laskea:

$\lim_x\rightarrow 2x$ Ratkaisu

$\lim_x\rightarrow 2x=2$

5. Funktion bondastin tuoteraja

Tässä tapauksessa vakio menee rajasta ja liikkuu sen moninkertaistamiseksi, kuten tämä:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Esimerkki

Laske, jos se on olemassa, seuraava raja:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Ratkaisu

Vakio 5 on ulkona lisääntymässä rajaan ja korvaavaa ominaisuutta käytetään:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Summaraja

Kahden toiminnon summan raja F ja g Se on rajojen summa:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Esimerkki

Etsi seuraava raja, jos se on olemassa:

Voi palvella sinua: Aseta teoria: Ominaisuudet, elementit, esimerkit, harjoitukset

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Ratkaisu

Rajojen summan ominaisuutta sovelletaan ensin ja sitten suoran korvauksen, koska operaatioissa ei ole vaikeuksia:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Vähennysraja

Kahden funktion vähentämisen rajan tapauksessa etene analogisella tavalla, että summan suhteen: Vähennysraja on rajojen vähentäminen:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Esimerkki

Laske seuraava raja:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Ratkaisu

Kahden toiminnon vähennysrajan ominaisuus sovelletaan ja sitten suora korvaus, koska kaikki toiminnot voidaan suorittaa ilman ongelmia:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Tuotesaja

Kahden toiminnon tuoteraja F ja g Se on rajojen tuote:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Esimerkki

Laske tämä raja:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Ratkaisu

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Osamäärän suhde

Kahden funktion suhteen raja F ja g Se on rajojen osoitus, edellyttäen, että g (x): n raja, kun x → c on erilainen kuin 0, koska jakoa 0 ei ole määritelty. Niin:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Esimerkki

Laske, jos se on olemassa, seuraavan rajan arvo:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Ratkaisu

Ensinnäkin omaisuusrajaominaisuutta sovelletaan rajojen osamäärän saamiseksi:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Korvaavaa ominaisuutta käytetään nyt jokaisen rajan löytämiseen:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Ja koska b ≠ 0, etsittu raja on osamäärä A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Raja

Eksponentin n voiman raja vastaa mainitulle voimaan nostettua rajaa seuraavasti:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Tapaus 1: X -tehon raja

Jos sinulla on esimerkiksi X -virran raja, tulokset:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Kiinteistön 4 mukaan tämä raja on:

Voi palvella sinua: Numeeriset analogiat: Tyypit, sovellukset ja harjoitukset

$\lim_x \rightarrow c x^n=c^n$

Tapaus 2: Juuriraja

N-tämä juuri voidaan kirjoittaa murto-eksponentin muodossa, joten:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Tärkeä: Jos juurihakemisto on tasainen, on välttämätöntä, että F (x): n raja, kun x → c on suurempi tai yhtä suuri kuin 0, koska negatiivisia määriä ei ole todellisia pareja.

Esimerkit

Määritä edellisten ominaisuuksien soveltaminen seuraavat rajat, jos niitä on:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Liittää jhk

Sen saadun vallan rajan ja suoran korvaamisen rajan mukaan:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Ratkaisu b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

yksitoista. Raja

Eksponentiaalisen B: n ja eksponentin F (x) rajan löytämiseksi funktion f (x) funktion perusta on nostettava seuraavasti:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Esimerkki

Selvitä, onko seuraava raja:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Ratkaisu

Tässä rajassa emä on numero E ja funktio f (x) = x², Siksi sinun on ensin laskettava X -raja² Kun x on taipumus 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Sitten sovelletaan eksponentiaalisen rajan ominaisuutta:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Eksponentiaalinen potentiaalinen funktioraja

Raja, kun funktion f (x) x → c, joka puolestaan on nostettu toiseen funktioon g (x) ilmaistaan:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Esimerkki

Laske seuraava raja, jos se on olemassa:

$\lim_x \rightarrow -1 (x-1)^^2x$

Ratkaisu

Edellisen ominaisuuden soveltamiseksi ne tunnistetaan ensin f (x) = x-1 ja g (x) = 2x ja sitten vastaavat rajat lasketaan:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Lopuksi:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Viitteet

Ayres, f. 2000. Laskeminen. 5DED. MC Graw Hill.
Leithold, L. 1992. Laskenta analyyttisellä geometrialla. Harla, S.-Lla.
Ilmaiset matematiikan tekstit. Rajat. Toipunut: matematiikka.Libretext.org.
Matematiikka. Lait ja rajoittaa kiinteistöjä. Toipunut: Matemovil.com.
Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen. Meksiko: Pearson Education.
Maailmankaikkeuden kaavat. Rajoittaa ominaisuuksia. Toipunut: UniversOformulat.com

Rajoita ominaisuuksia (esimerkkien kanssa)

1. Suoran vaihtoraja

Esimerkki

Ratkaisu

2. Rajan ainutlaatuisuus

Esimerkki

Ratkaisu

3. Vakio

Esimerkki

Ratkaisu

4. Identiteettifunktioraja

Esimerkki

Ratkaisu

5. Funktion bondastin tuoteraja

Esimerkki

Ratkaisu

6. Summaraja

Esimerkki

Ratkaisu

7. Vähennysraja

Esimerkki

Ratkaisu

8. Tuotesaja

Esimerkki

Ratkaisu

9. Osamäärän suhde

Esimerkki

Ratkaisu

10. Raja

Tapaus 1: X -tehon raja

Tapaus 2: Juuriraja

Esimerkit

Liittää jhk

Ratkaisu b

yksitoista. Raja

Esimerkki

Ratkaisu

12. Eksponentiaalinen potentiaalinen funktioraja

Esimerkki

Ratkaisu

Viitteet

Parhaat artikkelit

100 parasta ystävää laissa

Jätän sinulle parhaat oikeiden ystävien lauseet (ilman sitoutumista Espanjassa), romanttinen komedia...

Lola Van Wagenen Biography

Lola Van Wagenen (joulukuu 1938) on amerikkalainen historioitsija, joka oli Consumer Action Now -yri...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Rajan ainutlaatuisuus

$\lim_x\rightarrow 1\pi$ Ratkaisu

$\lim_x\rightarrow 2x$ Ratkaisu

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Esimerkki

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Ratkaisu

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Ratkaisu

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Ratkaisu

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Esimerkki

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Ratkaisu

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Tapaus 1: X -tehon raja

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Ratkaisu

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Viitteet