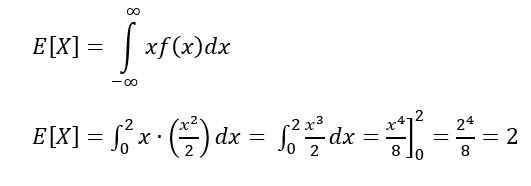Jatkuva satunnaismuuttuja

Selitämme, mikä jatkuva satunnaismuuttuja, sen ominaisuudet, esimerkit ja ratkaistu harjoitus on

Mikä on jatkuva satunnaismuuttuja?

Eräs Jatkuva satunnaismuuttuja Se on satunnaisesti saatu numeerinen arvo, joka johtuu kokeen tekemisestä ja voi ottaa äärettömiä arvoja. Tämä tarkoittaa, että muuttujan kaksi peräkkäistä arvoa on aina mahdollista löytää uusi väliarvo.

Koska sinulla on ääretön määrä arvoja, jatkuvien muuttujien arvojen kokoelma ei ole kirjanpito ja kuuluu melkein aina reaalilukujoukkoon.

Esimerkkejä tämän tyyppisistä muuttujista ovat ihmisen kyky, paino ja kehon lämpötila, mutta lukemattomia niistä voidaan määritellä, alla on useita esimerkkejä. Toisin kuin jatkuva satunnaismuuttuja, on olemassa huomaamaton satunnaismuuttuja, joka on kirjanpito, kuten perheen tyttäreiden lukumäärä tai kuinka monta autoa virasto myy yhden kuukauden kuluttua.

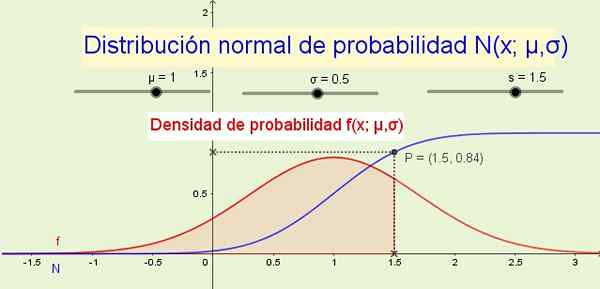
Diskreetti satunnaismuuttujat seuraavat usein normaalia todennäköisyysjakaumaa. Lähde: f. Zapata.

Jatkuva satunnaismuuttuja on merkitty härän kirjaimella, kuten X, ja muuttujan omaavat äärettömät arvot ovat satunnaisen kokeen mahdolliset tulokset:

X = x₁, x₂, x₃,… ∞

Jokaisella arvolla on tietty esiintymisen todennäköisyys, ja malliin, jolla tämä todennäköisyys lasketaan, sitä kutsutaan todennäköisyysjakauma.

Mutta koska X ottaa äärettömät arvot, muuttujan tiettyjen arvojen todennäköisyys ei voida laskea. Joten on välttämätöntä määritellä funktio F (x), nimeltään kertynyt jakelufunktio, tai yksinkertaisesti jakelufunktio, jonka mukaan kertynyt todennäköisyys lasketaan tiettyyn arvoon tai kahden arvon välillä:

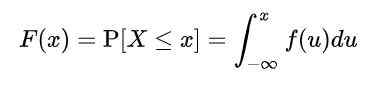
Missä f (u) saada nimi tiheysfunktio. Määritelty tällä tavalla, F (x) edustaa todennäköisyyttä, että X on välissä -∞ ja x.

Jatkuvan satunnaismuuttujan ominaisuudet

Jatkuvat satunnaismuuttujat ovat täydellisiä f (x).

Tiheysfunktio f (x) Täytyy täyttää seuraavat kiinteistöt:

• Toiminto f (x) Se on positiivinen: f (x)> = 0
• Käyrän alla oleva alue y = f (x) Se on aina yhtä suuri kuin yksi, toisin sanoen jonkin tuloksen esiintymisen todennäköisyys x Aikavälillä (-∞, +∞) on 100%.
• Todennäköisyys, että x on aikavälillä [a, b], lasketaan seuraavalla määritellyllä integraalilla:

Voi palvella sinua: Curtory: Määritelmä, tyypit, kaavat, mitä se on esimerkiksi

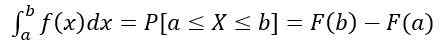
Joka vastaa käyrän alla olevaa aluetta y = f (x), ymmärtää -lla ja b -. Sitä paitsi:

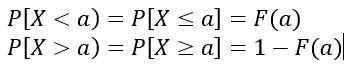
Arvot f (x) Ne eivät edusta todennäköisyyttä, joten P [x = c] = 0. Asiaankuuluvat arvot ovat käyrän alla olevaa aluetta vastaavat y = f (x), jotka edustavat todennäköisyyttä.

• Johdattamalla jakelufunktio F (x) kunnioittaen x, saadaan f (x).

Kaavio f (x) Jatkuvalle satunnaismuuttujalle se on analoginen taajuuden monikulmion kanssa, joka on rakennettu erilliselle tilastolliselle muuttujalle, erolla, että satunnaismuuttujalle välin leveys muuttuu äärettömäksi.

Toivoa

Toivo on yksi jatkuvan muuttujan ominaismittauksista. Toivo tai odotettu arvo X Osoittaa arvon, jonka odotetaan tapahtuvan useammin, ja se lasketaan seuraavan integraalin kautta:

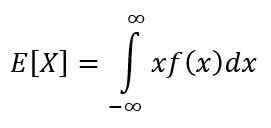
Sen ominaisuudet ovat:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Missä määrät -lla ja b - Ne ovat todellisia numeroita.

Esimerkit

Kuten aiemmin on osoitettu, on monia tilanteita, joissa yksi tai useampi jatkuva satunnaismuuttuja voidaan määritellä. Tieteillä ja muilla alueilla yleisimmät ovat ajan, pituuden, painon, tilavuuden ja lämpötilan:

Aika

Prosessien ja palveluiden optimoimiseksi on suunniteltu kokeita, joissa tutkitaan niiden toteuttamista koskevaa aikaa:

X = aika, joka vie asiakkaan pankkiikkunaan.

Y = mikä vie pikaruokapaikan tilauksen tarjoamisessa.

Z = aika, jolloin tietty kemiallinen reaktio tapahtuu.

Ja painot

Monissa ihmisissä ja eläimissä olevissa tutkimuksissa arkistot ja painot ovat merkityksellisiä:

X = tyttöjen korkeus kuudennessa kurssissa. Tutkinto jokaisessa koulussa kaupungissa.

Voi palvella sinua: Yhteydet: Yhteydet hahmot, kriteerit, esimerkit, harjoitukset

Y = vauvojen paino syntyessään julkisessa sairaalassa.

Z = Lehmien paino maatilalla.

Lämpötila

Lämpötila on merkityksellinen parametri lukuisissa kemiallisissa prosesseissa, jotka yleensä vievät äärettömät arvot tietyllä alueella:

X = lämpötila, jossa tietty kemiallinen reaktio tapahtuu, tietäen, että tämä tapahtuu välillä 80 ºC - 120 ºC.

Ratkaisut

Harjoitus 1

Määritä, mitkä ovat jatkuvat satunnaismuuttujat:

1. Yliopiston kahviin osallistuvien opiskelijoiden lukumäärä päivittäin.
2. Keskeistä potilaille tulevien potilaiden verenpaine.
3. Lintusiipien pituus uhanalaisista lajista, jotka asuvat varannossa.
4. Yhden henkilön ja toisen välillä käsitellään pankissa.
5. Viallisten tuotteiden määrä kuukaudessa tehtaalla.
6. Kolesterolitasot maatilan kanoilla.
7. Kadunvalaisimien määrä kadulla, yhteensä 12.

Ratkaisu

1.- Päivään osallistuvien opiskelijoiden lukumäärä on tunnoton, joten tämä muuttuja ei ole jatkuva, vaan hienovarainen.

2.- Se on jatkuvaa. Potilaiden verenpaine voi ottaa minkä tahansa arvon tietyllä alueella.

3.- Jatkuva muuttuja, koska linnun siipin pituus ottaa minimin ja maksimin välillä lajista riippuen.

4.- Asiakaspalvelun välinen aika on muuttuva ja voi ottaa minkä tahansa arvon tietyllä alueella, esimerkiksi välillä 1–5 minuuttia.

5.- Koska viallisten tuotteiden lukumäärä on kirjanpito, se on hienovarainen satunnaismuuttuja.

6.- Tämä muuttuja on jatkuvaa, koska kanojen kolesterolitaso vie minkä tahansa arvon aiemmin määritetyllä alueella.

Voi palvella sinua: Täydentävät kulmat: mitkä ja miten ne lasketaan, esimerkkejä, harjoituksia

7.- Hienotunteinen. Työvalaistusvalojen lukumäärä on kirjanpidon määrä.

Harjoitus 2

Jatkuva satunnaismuuttuja on määritelty X = "kolesterolitaso " Tietyllä maatilan kanoilla, jolla on seuraava tiheysfunktio f (x)-

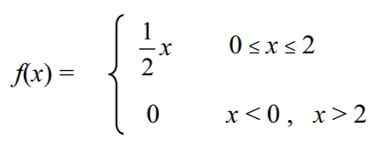
Laske seuraava:

1. F (x)
2. P [x ≤2]
3. Toivo Esim

Liittää jhk

Alussa annetun määritelmän mukaan:

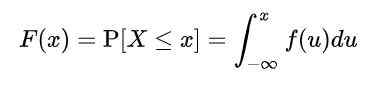
Siksi, F (x) Se on toiminto osissa. Aikavälille x<0, F (x) Se on yhtä suuri kuin 0, alussa ilmoitetuille ominaisuuksille.

Välein 0 -≤x≤2, Määrittelemätön integraali on ratkaistu:

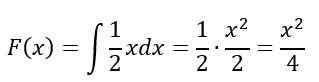
Lopuksi aikavälillä x> 2, F (x) = 1, Ominaisuuksien mukaan siksi, F (x) Se pysyy näin:

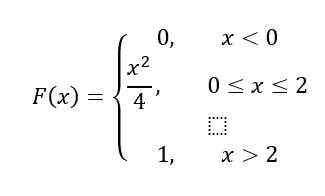
Ratkaisu b

Haluttu todennäköisyys on F (1.2) ja como x = 1.2 Se löytyy välillä 0 -≤x≤2, se osa F (x) Arvioida:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Liuos C

Toivon tai odotetun arvon laskemiseksi sitä käytetään: