Ryhmitetyt data -esimerkit ja ratkaistu harjoitus

Se ryhmitelty tieto He ovat ne, jotka ovat luokiteltu luokkiin tai luokkiin, ottaen kriteerit taajuutensa. Tämä tehdään tarkoituksena yksinkertaistaa suurten tietojen hallintaa ja niiden suuntausten määrittäminen.

Kun tiedot on järjestetty näihin luokkiin, tiedot muodostavat a Taajuusjakauma, josta hyötytiedot poistetaan sen ominaisuuksien kautta.

Kuvio 1. Ryhmitetyillä tiedoilla voit rakentaa grafiikkaa ja laskea tilastollisia parametreja, jotka kuvaavat suuntauksia. Lähde: Pixabay.

Seuraavaksi näemme yksinkertaisen esimerkin ryhmiteltyistä tiedoista:

Oletetaan, että 100 yliopiston perusfysiikan keskuudessa valitun 100 naisopiskelijan paikka mitataan ja saadaan seuraavat tulokset:

Saadut tulokset jaettiin viiteen luokkaan, jotka näkyvät vasemmassa sarakkeessa.

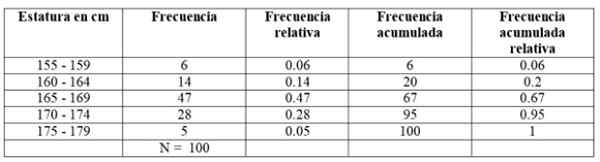
Ensimmäisessä luokassa, välillä 155–159 cm, on 6 opiskelijaa, toisessa luokassa 160 - 164 cm on 14 opiskelijaa, kolmas luokka 165 - 169 cm on suurin jäsenten lukumäärä: 47. Seuraa sitten luokkaa 170-174 cm 28 opiskelijan kanssa ja lopulta yksi vuosina 175-179 cm vain 5: llä.

Kunkin luokan jäsenten lukumäärä on juuri taajuus jompikumpi Absoluuttinen freekuusia Ja lisäämällä ne kaikki saadaan kokonaistiedot, mikä tässä esimerkissä on 100.

[TOC]

Taajuuden jakautumisominaisuudet

Taajuus

Kuten olemme nähneet, taajuus on kuinka monta kertaa tosiasia toistetaan. Ja jakautumisominaisuuksien, kuten keskiarvon ja varianssin, laskelmien helpottamiseksi seuraavat määrät on määritelty:

-Kertynyt taajuus: Se saadaan lisäämällä luokan taajuus, jolla on etuosa kertynyt taajuus. Ensimmäinen taajuudet osuvat kyseisen aikavälin taajuuteen, ja viimeinen on tietojen kokonaismäärä.

-Suhteellinen taajuus: Se lasketaan jakamalla kunkin luokan absoluuttinen taajuus tietojen kokonaismäärällä. Ja jos kertomalla 100: lla, sinulla on prosenttiosuusprosentti.

Voi palvella sinua: vektoritoiminnot

-Kertynyt suhteellinen taajuus: Se on kunkin luokan suhteellisten taajuuksien summa edellisen kertyneen kanssa. Viimeisen kertyneistä suhteellisista taajuuksista on oltava yhtä suuri kuin 1.

Esimerkiksi taajuudet ovat tällaisia:

Rajat

Kunkin luokan tai aikavälin ääriarvoja kutsutaan Luokkarajat. Kuten voimme nähdä, jokaisella luokalla on alaraja ja yksi suurempi. Esimerkiksi arkistoa koskevan tutkimuksen ensimmäisen luokan raja on alle 155 cm ja yksi yli 159 cm.

Tässä esimerkissä on rajat, jotka on selvästi määritelty, mutta se on mahdollista.

Rajat

Korkeus on jatkuva muuttuja, joten voidaan katsoa, ​​että ensimmäinen luokka alkaa vuonna 154.5 cm, koska pyöristämällä tämä arvo lähimpään kokonaislukuun, saadaan 155 cm.

Tämä luokka kattaa kaikki arvot jopa 159.5 cm, koska tästä artikkelista on pyöristetty 160: een.0 cm. Kohta 159.7 cm kuuluu jo seuraavaan luokkaan.

Tämän esimerkin todelliset luokan rajat ovat CM: ssä:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitudi

Luokan leveys saadaan vähentämällä rajat. Esimerkimme ensimmäisessä aikavälillä sinulla on 159.5 - 154.5 cm = 5 cm.

Lukija voi varmistaa, että esimerkin muille väliajoille amplitudi johtuu myös 5 cm: stä. On kuitenkin huomionarvoista, että jakaumat voidaan rakentaa erilaisilla amplitudilla.

Se voi palvella sinua: sääntö t: Ominaisuudet, niin että se on esimerkkejä

Luokan tuotemerkki

Se on aikavälin keskipiste ja saadaan keskimäärin ylärajan ja alarajan välillä.

Esimerkiksi ensimmäisen luokan tuotemerkki on (155 + 159)/2 = 157 cm. Lukija voi varmistaa, että jäljellä olevat luokan tuotemerkit ovat: 162, 167, 172 ja 177 cm.

Luokkabrändien määrittäminen on tärkeää, koska ne ovat välttämättömiä jakauman aritmeettisen keskiarvon ja varianssin löytämiseksi.

Keskeisen taipumuksen ja leviämisen mitat ryhmiteltyihin tietoihin

Ylittävimmät keskeiset taipumusmittaukset ovat keskimäärin, mediaani ja muoti, ja kuvaavat tarkalleen tiettyjen keskusarvojen ryhmitettävien tietojen taipumusta.

Puoli

Se on yksi tärkeimmistä keskeisistä taipumusmittauksista. Ryhmitetyissä tiedoissa aritmeettinen keskiarvo voidaan laskea kaavalla:

 Missä:

-X on keskiarvo

-F_Yllyttää on luokan taajuus

-m_Yllyttää Se on luokan tuotemerkki

-G on luokkien lukumäärä

-n on tietojen kokonaismäärä

Mediaani

Mediaanille sinun on tunnistettava aika, jossa havainto N/2 sijaitsee. Esimerkissämme tämä havainto on numero 50, koska tietoja on yhteensä 100. Tämä havainto on aikavälillä 165-169 cm.

Sitten sinun on interpoloida löytääksesi kyseistä havaintoa vastaavan numeerisen arvon, jota varten kaavaa käytetään:

Missä:

-C = väliaikaisen leveys, jossa mediaani sijaitsee

-B -_M = Sen välin alaraja, johon mediaani kuuluu

-F_m = Mediaanivälin havaintojen määrä

-N/2 = puolet kokonaistiedoista

-F_Bm = Havaintojen kokonaismäärä ennen mediaanin väliä

Muoti

Muodille tunnistetaan modaaliluokka, joka sisältää suurimman osan havainnoista, joiden luokkabrändi tunnetaan.

Voi palvella sinua: kuusikulmainen pyramidi

Varianssi ja keskihajonta

Varianssi ja keskihajonta ovat dispersiomittauksia. Jos tarkoitamme varianssia S: n kanssa² Ja standardipoikkeamaan, joka on varianssin neliöjuuri S: ksi, ryhmitetyille tiedoille, joita meillä on:

JA

Liikuntaa

Laske alussa ehdotettujen yliopisto -opiskelijoiden aseman jakautumisen arvot:

a) keskimäärin

b) väliaine

c) muoti

d) varianssi ja keskihajonta.

Kuva 2. Kun kyse on monista arvoista, kuten suuren opiskelijaryhmän, on edullista ryhmitellä tietoihin luokkiin. Lähde: Pixabay.

Liittää jhk

Rakennetaan seuraava taulukko laskelmien helpottamiseksi:

Yllä ryhmitelty keskimääräisen ryhmän ilmaisun kautta:

Arvojen korvaaminen ja summan suorittaminen suoraan:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Ratkaisu b

Väli, johon mediaani kuuluu, on 165-169 cm, koska se on useimmiten aikaväli.

Tunnistamme kaikki nämä arvot esimerkissä taulukon 2 avulla:

C = 5 cm (katso amplitudiosa)

B -_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_Bm = 20

Korvaaminen kaavassa:

Liuos C

Useimmissa havainnoissa sisältyvä aika on 165-169 cm, jonka luokkabrändi on 167 cm.

Liuos D

Laajennamme edellistä taulukkoa lisäämällä kaksi ylimääräistä sarakketta:

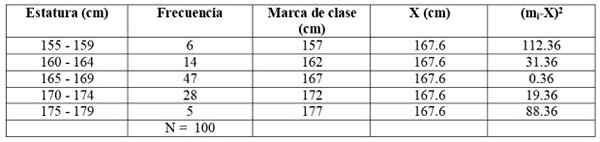
Käytämme kaavaa:

Ja kehitämme summan:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Siksi:

S = √21.35 cm² = 4.6 cm

Viitteet

1. Berenson, m. 1985. Hallinnon ja taloustieteen tilastot. Inter -American S.-Lla.
2. Canavos, G. 1988. Todennäköisyys ja tilastot: Sovellukset ja menetelmät. McGraw Hill.
3. DeVore, J. 2012. Tekniikan ja tieteen todennäköisyys ja tilastot. Kahdeksas. Painos. Kyynärmä.
4. Levin, r. 1988. Järjestelmänvalvojien tilastot. Toinen. Painos. Prentice Hall.
5. Spiegel, M. 2009. Tilastot. Schaum -sarja. 4 ta. Painos. McGraw Hill.
6. Walpole, r. 2007. Tekniikan ja tieteen todennäköisyys ja tilastot. Pearson.