Mikä on dynaaminen tasapaino? (Esimerkki)

Hän dynaaminen tasapaino Se on tila, jossa liikkuva esine on ihanteellisesti edustettuna hiukkasena, kun sen liike on tasainen välilasvainen. Tämä ilmiö tapahtuu, kun siihen vaikuttavien ulkoisten joukkojen summa peruutetaan.

Yleensä uskotaan, että jos esineellä ei ole netto- tai tuloksena olevaa voimaa, lepo on ainoa mahdollinen seuraus. Tai myös se, että ruumiin olisi tasapainossa, ei pitäisi olla voimaa.

Kuvio 1. Tämä kissa liikkuu dynaamisessa tasapainossa, jos se tekee sen vakiona nopeudella. Lähde: Pixabay.

Itse asiassa tasapaino on kiihtyvyyden puuttuminen, ja siksi vakio nopeus on täysin mahdollista. Kuvan kissa voi liikkua ilman kiihtyvyyttä.

Kohde, jolla on tasainen pyöreä liike, ei ole dynaamisessa tasapainossa. Vaikka sen nopeus on vakio, ympärysmiipan keskustaan ​​on suunnattu kiihtyvyys, joka pitää sen radalla. Tämä kiihtyvyys on vastuussa vaihtamisesta nopeusvektoriin.

Null -nopeus on erityinen hiukkasten tasapainon tilanne, mikä vastaa vakuuttamista, että esine on levossa.

Mitä tulee objektien pitämiseen hiukkasena, se on erittäin hyödyllinen idealisointi kuvaamalla niiden globaalia liikettä. Oikeastaan ​​meitä ympäröivät liikkuvat esineet koostuvat suuresta määrästä hiukkasia, joiden yksittäinen tutkimus olisi hankala.

[TOC]

Superpositioperiaate

Tämä periaate sallii korvata esineiden useiden voimien vaikutuksen vastaavalla, jota kutsutaan tuloksena olevaksi voiman kylmäksi tai nettovoima FN: lle ja joka tässä tapauksessa on mitätön:

F1 +f2 +f3 +… . = FR = 0

Missä pakottaa F1, F2, F3 .. ., Fi ovat kehossa toimivat erilaiset voimat. Sumory -merkintä on kompakti tapa ilmaista se:

Niin kauan kuin epätasapainoinen voima ei puutu, esine voidaan ylläpitää loputtomiin liikkumista vakiona nopeudella, koska vain voima voi muuttaa tätä panoraamaa.

Tuloksena olevan voiman komponenttien suhteen hiukkasen dynaaminen tasapainotila ilmaistaan ​​seuraavasti: fx = 0; Fy = 0; Fz = 0.

Kierto- ja tasapainoolosuhteet

Hiukkasmallissa ehto FR = 0 on riittävä tasapainotakuu. Kun otetaan huomioon tutkittavan matkapuhelimen mitat, on mahdollista, että esine voi kiertää.

Kiertoliike merkitsee kiihtyvyyden olemassaoloa, joten pyörivät kappaleet eivät ole dynaamisessa tasapainossa. Kehon käännös ei tarvitse vain voiman osallistumista, vaan on välttämätöntä soveltaa kätevää paikkaa.

Sen tarkistamiseksi voit sijoittaa ohuen pituuden sauvan kitkan, kuten jäisen pinnan tai erittäin kiillotetun peilin tai lasin, pinnalle. Normaalit tasapainot painon pystysuunnassa ja samalla kun kahta voimaa F1 ja F2, seuraavan kuvan kaavion mukaan, mitä tapahtuu: mitä tapahtuu:

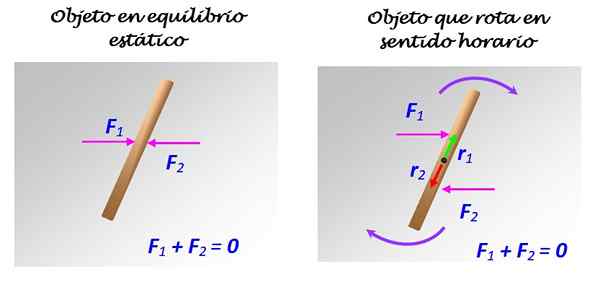Kuva 2. Sauva pinnalla ilman kitkaa voi olla tasapainossa riippuen siitä, kuinka voimia 1 ja 2 käytetään. Lähde: Itse tehty.

Jos F1 ja F2 sovelletaan vasemmalla esitetyllä tavalla, yhteisella toimintalinjalla, sauva pysyy levossa. Mutta jos F1 ja F2 sovelletaan oikealle esitetyllä tavalla, eri toimintaviivoilla, vaikka rinnakkain, kierto tapahtuu aikataulussa, akselin ympärillä, joka kulkee keskustan läpi.

Tässä tapauksessa F1 ja F2 muodostavat pari voimaa tai yksinkertaisesti pari.

Vääntömomentti tai voimamomentti

Vääntömomentin vaikutuksena on tuottaa kierto laajennetulle esineelle, kuten esimerkkitangasta. Väl. Se on merkitty τ ja se lasketaan:

τ = r x f

Tässä lausekkeessa F on käytetty voima ja R on vektori, joka siirtyy kierto -akselista voiman levityspisteeseen (katso kuva 2). Τ: n suunta on aina kohtisuorassa koneeseen, jossa f ja r valhe ja sen yksiköt kansainvälisessä järjestelmässä ovat n.m.

Esimerkiksi F1: n ja F2: n tuottamien momenttien suunta on kohti paperia, vektorituotteen sääntöjen mukaan.

Vaikka joukot peruuttavat toisiaan, heidän vääntömomentinsa eivät. Ja tulos on esitetty kierto.

Tasapainoolosuhteet laajennetulle esineelle

Nämä ovat kaksi ehtoa, jotka on täytettävä laajennetun objektin tasapainon takaamiseksi:

Ratkaistu esimerkki

Sinulla on laatikko tai tavaratila, joka painaa 16 kg-F: tä, joka liukuu kallistetun tason läpi vakiona nopeudella. Kiilan kaltevuuskulma on θ = 36º. Vastaa:

a) Mikä on tavaratilan liukuminen vakiona nopeudella tarvittavan dynaamisen kitkavoiman suuruus?

b) kuinka paljon kineettinen kitkakerroin on?

c) Jos kaltevan tason korkeus H on 3 metriä, etsi tavaratilan laskeutumisnopeus tietäen, että maan saavuttaminen vie 4 sekuntia.

Ratkaisu

Tavarausta voidaan käsitellä ikään kuin se olisi hiukkas. Siksi voimat sovelletaan noin sen keskustassa sijaitsevaan pisteeseen, johon kaikki sen massa voidaan olettaa. Juuri tähän pisteeseen seurataan.

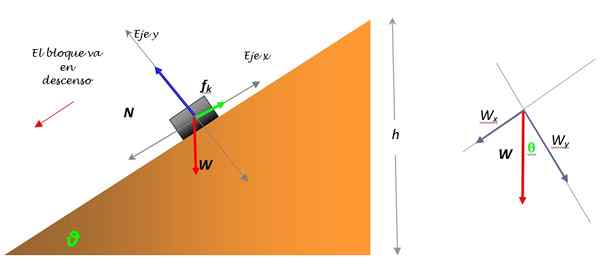Kuva 3. Vapaa runkokaavio tavaratilasta, joka liukuu alamäkeen ja painon hajoamiseen (oikea). Lähde: Itse tehty.

Paino W on ainoa voima, joka ei putoa yhdelle koordinaattiakselista ja joka on jaettu kahteen komponenttiin: WX ja WY. Tämä hajoaminen on esitetty kaaviossa (kuva 3).

On myös kätevää siirtää paino kansainvälisen järjestelmän yksiköille, jolle riittää moninkertaistaa 9: llä.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Osa A

Koko vaaka -akselilla on WX -painon vaakasuora komponentti ja FK: n dynaaminen tai kineettinen kitkavoima, joka vastustaa liikettä.

Positiivisen merkityksen valitsemalla liikkeen suuntaa, on helppo huomata, että se on WX vastuussa lohkosta alamäkeen. Ja koska kitka vastustaa, sen sijaan, että liukuu nopeasti, lohkolla on mahdollisuus liukua jatkuvasti alamäkeen.

Ensimmäinen tasapainotila on riittävä, koska käsittelemme tavaratilaa hiukkasena, joka on varmistettu dynaamisessa tasapainossa:

WX - FK = 0 (vaakasuorassa osoitteessa ei ole kiihtyvyyttä)

FK = 92.2 n

Osa B

Dynaamisen kitkan suuruus on vakio ja se annetaan fk = μk n. Tämä tarkoittaa, että dynaaminen kitkavoima on verrannollinen normaaliin ja tämän suuruus on tarpeen kitkakertoimen tuntemiseksi.

Tarkkailemalla vapaata runkokaaviota voidaan nähdä, että pystysuoralla akselilla meillä on normaali voima n, jonka kiila käyttää tavaratilaan ja on suunnattu ylöspäin. Hän on tasapainossa painon pystysuuntaisen komponentin kanssa. Valitseminen positiiviseksi merkitykseksi ja Newtonin toisen lain ja tasapainon tilan tulokset: hyödyntäminen:

N - WY = 0 (pystysuoraa akselia pitkin ei ole liikettä)

Siksi:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2/126.9 = 0.73

Kohta C

Tavaran kokonaismatka kiilan yläosasta maahan löytyy trigonometrialla:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

Nopeuden laskemiseksi käytetään yhtenäisen suorakulmaisen liikkeen määritelmää:

V = d/t = 5.1 m/4 s = 1.3 m/s

Viitteet

1. Rex, a. 2011. Fysiikan perusteet. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen. 120 - 124.
3. Serway, R., ULOLE, c. 2011. Fysiikan perusteet. 9na ed. Cengage -oppiminen. 99-112.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fysiikka. Addison Wesley. 148-164.