Mikä on suhteellisuuskerroin? (Ratkaisut harjoitukset)

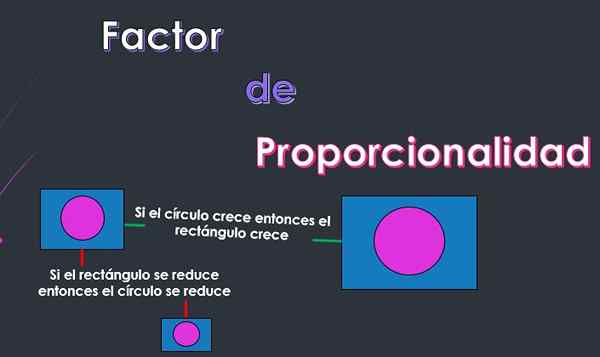
Hän suhteellisuuskerroin o Suhteellisuusvakio on luku, joka osoittaa, kuinka paljon toinen esine muuttuu suhteessa ensimmäisen objektin kärsimään muutokseen.

Esimerkiksi, jos sanotaan, että portaikon pituus on 2 metriä ja että tämä projisoima varjo on 1 metri (suhteellisuuskerroin on 1/2), niin jos portaikko on vähennetty 1 metrin pituuteen, Varjo vähentää sen pituutta suhteellisesti, siksi varjon pituus on 1/2 metriä.

Jos päinvastoin, portaikko nostetaan arvoon 2.3 metriä silloin varjon pituus on 2.3*1/2 = 1.15 metriä.

Suhteellisuus on vakio suhde, joka voidaan luoda kahden tai useamman objektin välillä siten.

Esimerkiksi, jos sanotaan, että kaksi objektia on sen pituuden suhteen verrannollinen, sillä on, jos objekti kasvaa tai vähentää sen pituutta, niin toinen esine lisää tai vähentää sen pituutta suhteellisesti.

Suhteellisuuskertoimen käsite

Suhteellisuuskerroin on, kuten yllä olevassa esimerkissä esitetään, vakio, jolla on kerrottava toisen suuruuden saamiseksi.

Edellisessä tapauksessa suhteellisuuskerroin oli 1/2, koska ”X” -portaat mitattiin 2 metriä ja varjo “Y” mitattu 1 metri (puoli). Siksi sinun täytyy y = (1/2)*x.

Joten kun "x" muuttuu, niin "Y" muuttuu myös. Jos se on "y", se muuttuu myös "x" muuttuu myös, mutta suhteellisuuskerroin on erilainen, siinä tapauksessa se olisi 2.

Suhteellisuusharjoitukset

- Ensimmäinen harjoitus

Juan haluaa valmistaa kakun 6 henkilölle. Juanin resepti sanoo, että kakkulla on 250 grammaa jauhoja, 100 grammaa voita, 80 grammaa sokeria, 4 munaa ja 200 millilitraa maitoa.

Ennen kakun valmistelua, Juan tajusi, että hänen reseptinsä on kakku 4 henkilölle. Mikä pitäisi olla Juanin käytettävä suuruus?

Ratkaisu

Tässä suhteellisuus on seuraava:

4 ihmistä - 250 g jauhoja - 100 g voita - 80 g sokeria - 4 munaa - 200 ml maitoa

6 henkilöä -?

Suhteellisuuskerroin tässä tapauksessa on 6/4 = 3/2, joka voitaisiin ymmärtää ikään kuin se jaetaan ensin 4: llä ainesosien saamiseksi henkilöä kohden ja kerro sitten 6: lla kakun tekemiseksi 6 henkilölle.

Kertoamalla kaikki määrät 3/2, ainesosat ovat 6 henkilöä:

6 ihmistä - 375 g jauhoja - 150 g voita - 120 g sokeria - 6 munaa - 300 ml maitoa.

- Toinen harjoitus

Kaksi ajoneuvoa ovat identtiset paitsi renkaat. Ajoneuvon renkaiden säde on yhtä suuri kuin 60 cm ja toisen ajoneuvon renkaiden säde on yhtä suuri kuin 90 cm.

Jos kiertueen jälkeen sinun on annettava määrä kierroksia, jotka renkaat, joilla on vähemmän sädettä, oli 300 kierrosta. Kuinka monta käännöstä antoi suurimmat radiorenkaat?

Ratkaisu

Tässä harjoituksessa suhteellisuusvakio on yhtä suuri kuin 60/90 = 2/3. Joten jos radion pienet renkaat antoivat 300 kierrosta, korkeimman radion renkaat antoivat 2/3*300 = 200 kierrosta.

- Kolmas harjoitus

On tiedossa, että 3 työntekijää maalasi 15 -metrin seinän 5 tunnissa. Kuinka paljon he voivat maalata 7 työntekijää 8 tunnissa?

Ratkaisu

Tässä harjoituksessa toimitetut tiedot ovat:

3 työntekijää - 5 tuntia - 15 m² seinää

Ja mitä hän ihmettelee, on:

7 työntekijää - 8 tuntia -- ? Mökki.

Saatat kysyä, kuinka paljon 3 työntekijää maalasi 8 tunnissa? Tämän tuntemiseksi osuuskertoimen 8/5 toimittama tietorivi kerrotaan. Tämä osoittaa seurauksena:

3 työntekijää - 8 tuntia - 15*(8/5) = 24 m² seinää.

Nyt haluat tietää, mitä tapahtuu, jos työntekijöiden lukumäärä nostetaan 7: een. Tietää, mikä vaikutus tuottaa tekijän 7/3 maalatun seinän määrän. Tämä antaa lopullisen ratkaisun:

7 työntekijää - 8 tuntia - 24*(7/3) = 56 m² seinää.

Viitteet

1. Cofré, a., & Tapia, L. (tuhatyhdeksänsataayhdeksänkymmentäviisi). Kuinka kehittää matemaattinen looginen päättely. Yliopiston toimitus.
2. Edistynyt Telerasporte -fysiikka. (2014). Edu Nasz.
3. Giancoli, D. (2006). Fysiikan osa I. Pearson -koulutus.
4. Hernández, J. d -d. (S.F.-A. Matematiikan muistikirja. Kynnys.
5. Jiménez, J., Rofríguez, M., & Estrada, r. (2005). Matematiikka 1. syyskuuta. Kynnys.
6. Neuhauser, c. (2004). Tieteen matematiikka. Pearson -koulutus.
7. Peña, m. D -d., & Muntaner,. R -. (1989). Fysikaalinen kemia. Pearson -koulutus.
8. Segovia, b. R -. (2012). Matemaattinen toiminta ja pelit Miguelin ja Lucían kanssa. Baldomero Rubio Segovia.
9. Tocci, r. J -., & Widmer, N. S. (2003). Digitaaliset järjestelmät: Periaatteet ja sovellukset. Pearson -koulutus.