Trigonometriset rajat niiden ratkaisemiseksi, ratkaisut harjoitukset

Se trigonometriset rajat Ne ovat funktioiden rajoja siten, että nämä toiminnot muodostuvat trigonometrisillä funktioilla.

On kaksi määritelmää, jotka on tiedettävä ymmärtämään, kuinka trigonometrisen rajan laskeminen suoritetaan. Nämä määritelmät ovat:

- "F" -funktion raja, kun "x" taipumus "B": Se koostuu laskemalla arvo, jolla F (x) lähestyy "x" lähestyy "B", vakuuttamatta "B".

- Trigonometriset funktiot: Trigonometriset toiminnot ovat sin (x), cos (x) ja tan (x) merkitty sini-, kosini- ja tangenttifunktiot.

Muut trigonometriset toiminnot saadaan edellä mainitusta kolmesta toiminnasta.

Funktiot rajoitukset

Funktiorajan käsitteen selventämiseksi näytämme joitain esimerkkejä yksinkertaisilla toiminnoilla.

- F (x) = 3: n raja, kun "x" on taipumus "8" on yhtä suuri kuin "3", koska funktio on aina vakio. Ei ole väliä kuinka paljon "x" on arvoinen, F (x) -arvo on aina "3".

- F (x) = x-2: n raja, kun "x" on taipumus "6" on "4". Siitä lähtien, kun "X" on lähellä "6", sitten "x-2" lähestyy "6-2 = 4".

- G (x) = x²: n raja, kun "x" on taipumus "3" on yhtä suuri kuin 9, koska kun "x" lähestyy "3", sitten "x²" lähestyy "3² = 9".

Kuten aiemmissa esimerkeissä voidaan huomata, rajan laskeminen koostuu arvioinnin arvioinnista, jolle “x” yleensä on toiminnassa, ja tulos on rajan arvo, vaikka tämä pätee vain jatkuviin funktioihin.

Onko monimutkaisempia rajoja?

Vastaus on kyllä. Aikaisemmat esimerkit ovat yksinkertaisimmat esimerkit rajoista. Laskentakirjoissa päärajaharjoitukset ovat ne, jotka tuottavat tyypin 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 ja (∞)^0 määrittelemättömyyden.

Voi palvella sinua: Pythagorean -identiteetit: esittely, esimerkki, harjoitukset

Näitä lausekkeita kutsutaan määrittelyiksi, koska ne ovat ilmaisuja, joilla on matemaattisesti järkeä.

Lisäksi alkuperäiseen rajaan liittyvistä toiminnoista riippuen tulokset, jotka saadaan määrittelyjen ratkaisemiseksi, voi olla erilainen kussakin tapauksessa.

Esimerkkejä yksinkertaisista trigonometrisistä rajoista

Rajojen ratkaisemiseksi on aina erittäin hyödyllistä tietää mukana olevien toimintojen kuvaajat. Alla on sinus-, kosini- ja tangenttifunktioiden kaaviot.

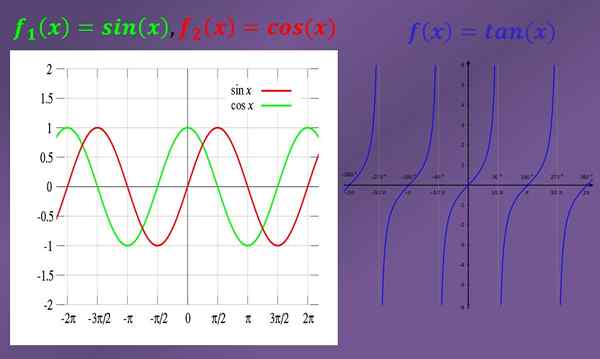
Joitakin esimerkkejä yksinkertaisista trigonometrisistä rajoista ovat:

- Laske ilman (x) raja, kun "x" on taipumus "0".

Kun näet kaavion, näet, että jos "X" lähestyy "0" (sekä vasemmalla että oikealla), niin rinnan grafiikka lähestyy myös "0". Siksi synnin raja (x), kun "x" on taipumus "0" on "0".

- Laske cos (x) -raja, kun "x" on taipumus "0".

Kosinin kuvaajan tarkkailu voidaan nähdä, että kun "X" on lähellä "0", kosinin kuvaaja on lähellä "1". Tämä tarkoittaa, että cos (x): n raja "x": llä on taipumus "0" on yhtä suuri kuin "1".

Raja voi olla (lukumäärä), kuten edellisissä esimerkeissä tapahtuu, mutta voi myös tapahtua, että sitä ei ole olemassa, kuten seuraavassa esimerkissä on esitetty.

- Tan (x) -raja, kun "x" on taipumus "π/2" vasemmalla on yhtä suuri kuin "+∞", kuten grafiikassa voidaan nähdä. Toisaalta ruskean (x) raja, kun "x" on taipumus "-π/2" oikealla on yhtä suuri kuin "-∞".

Trigonometrinen rajoitusidentiteetti

Kaksi erittäin hyödyllistä identiteettiä, kun trigonometrisiä rajoja lasketaan: ovat:

Voi palvella sinua: epälineaarinen ohjelmointi: menetelmät ja harjoitukset

- "Sin (x)/x" -raja "X" on taipumus "0" on yhtä suuri kuin "1".

- Raja "(1-cos (x))/x" kun "x" on taipumus "0" on yhtä suuri kuin "0".

Näitä identiteettejä käytetään hyvin usein, kun sinulla on jonkinlainen määrittelemätön.

Ratkaisut

Ratkaise seuraavat rajat edellä kuvattujen identiteettien avulla.

- Harjoitus 1

Laske rajan "f (x) = ilman (3x)/x" kun "x" on taipumus "0".

Jos F -funktio arvioidaan ”0”, saadaan tyypin 0/0 määrittelemättömyys. Siksi meidän on yritettävä ratkaista tämä määrittelemättömyys käyttämällä kuvattuja identiteettejä.

Ainoa ero tämän rajan ja identiteetin välillä on numero 3, joka näkyy sinifunktiossa. Identiteetin soveltamiseksi ”f (x)” -toiminto on kirjoitettava uudelleen seuraavasti: "3*(ilman (3x)/3x)". Nyt sekä rintojen argumentti että nimittäjä ovat yhtä suuret.

Joten kun "X" on taipumus "0", identiteetin käyttö on "3*1 = 3". Siksi F (x): n raja, kun "x" on taipumus "0" on yhtä suuri kuin "3".

- Harjoitus 2

Laske rajan ”g (x) = 1/x - cos (x)/x”, kun “x” on taipumus “0”.

Kun ”x = 0” korvataan g (x) tyypin ∞ -∞: n määrittelemättömyys. Sen ratkaisemiseksi fraktiot vähennetään, mikä antaa seurauksena "(1-cos (x))/x".

Nyt soveltamalla toista trigonometristä identiteettiä G (x): n raja on, että "X" on taipumus "0" on yhtä suuri kuin 0.

- Harjoitus 3

Laske "h (x) = 4tan (5x)/5x" "kun" x "on taipumus" 0 ".

Jälleen jos H (x) arvioidaan ”0”, tyypin 0/0 määrittelemättömyys saadaan.

Uudelleenkirjoittaminen nimellä (5x) kuten ilman (5x)/cos (5x), osoittautuu, että h (x) = (ilman (5x)/5x)*(4/cos (x))).

Se voi palvella sinua: Ympyrän kirjoitettu kulma: Määritelmä, lauseet, esimerkit

Tätä käyttämällä 4/cos (x) -raja, kun “X” on taipumus “0” on yhtä suuri kuin “4/1 = 4” ja saadaan ensimmäinen trigonometrinen identiteetti, että H (x): n raja, kun “X” on taipumus "0" on yhtä suuri kuin "1*4 = 4".

Havainto

Trigonometriset rajat eivät aina ole helppo ratkaista. Tässä artikkelissa esitettiin vain perusesimerkkejä.

Viitteet

1. Fleming, w., & Varberg, D. JA. (1989). Prealculus -matematiikka. Prentice Hall Ptr.
2. Fleming, w., & Varberg, D. JA. (1989). Precalculus-matematiikka: ongelmanratkaisutapa (2, kuvitettu ED.-A. Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Algebra ja trigonometria analyyttisellä geometrialla. Pearson -koulutus.
4. Larson, r. (2010). Esikuva (8 Ed.-A. Cengage -oppiminen.
5. Uskollinen, j. M., & Viloria, N. G. (2005). Litteä analyyttinen geometria. Mérida - Venezuela: Venezuelan toimituksellinen C. -Lla.
6. Pérez, c. D -d. (2006). Prequalculus. Pearson -koulutus.
7. Purcell, E. J -., Varberg, D., & Rigdon, S. JA. (2007). Laskeminen (Yhdeksäs ed.-A. Prentice Hall.
8. Saenz, J. (2005). Differentiaalilaskelma varhaisten transsendenttisten toimintojen kanssa tieteen ja tekniikan suhteen (Toinen painos ed.-A. Hypotenuusa.
9. Scott, c. -Lla. (2009). Cartesian lentokoneen geometria, osa: Analyyttiset kartiot (1907) (Uusintapainos ED.-A. Salamanlähde.
10. Sullivan, M. (1997). Prequalculus. Pearson -koulutus.