Mikä on nettovoima? (Esimerkkejä)
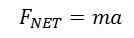
- 5188
- 492
- Joshua Emmerich
Se Nettovoima Se määritellään kaikkien esineeseen vaikuttavien voimien summaksi. Esimerkki? Pysäytä jalkapallopallo, pallo lähtee ja liikkuu ilman läpi. Tuolloin palloon toimii nettovoima. Kun pallo alkaa palata maahan ja lopulta pysähtyy, myös palloon toimii nettovoima.
Newtonin toisessa laissa sanotaan, että "kun nettovoima toimii esineeseen, niin kyseistä esinettä on kiihdytettävä, ts. Sen nopeus muuttuu toisesta toiseen". Kun potket jalkapallopalloa ensimmäistä kertaa, se kiihtyy ja kun jalkapallopallo alkaa pysähtyä, kunnes se pysähtyy, se myös kiihtyy.
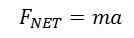
Esineeseen voi olla useita voimia, ja kun kaikki nämä voimat lisätään, tulos on se, mitä kutsumme esineeseen toimivaksi nettovoimaksi.
Jos nettovoima lisää nollaan, esine ei kiihdy, siksi se liikkuu vakiona nopeudella. Jos nettovoima lisää eri arvoa nolla, objekti kiihtyy.
Luonnossa kaikki voimat vastustavat muita voimia, kuten kitka tai vastakkaiset painovoimat. Voimat voivat aiheuttaa kiihtyvyyttä vain, jos ne ovat suurempia kuin vastakkaiset voimat.
Jos voima työntää esineen, mutta se yhdistää kitka, esine ei kiihdytä. Samoin, jos voima työntyy painovoimaa vastaan, mutta on pienempi kuin esineen painovoima, se ei kiihdytä.
Esimerkiksi, jos objektin 15-Newton-työntövoima on päinvastainen 10-Newtonin kitkavoiman avulla, esine kiihtyy ikään kuin 5-Newtonin nettovoima ilman kitkaa voitaisiin työntää.
[TOC]
Newtonin toinen laki
Newtonin ensimmäisen liikkeen laki ennustaa esineiden käyttäytymisen, joille kaikki nykyiset voimat ovat tasapainossa.
Voi palvella sinua: pneumaattinen järjestelmäEnsimmäisessä laissa, jota joskus kutsutaan hitauslakiin), todetaan, että jos esineeseen vaikuttavat voimat ovat tasapainossa, niin kyseisen esineen kiihtyvyys on 0 m / s / s. Tasapainon kohteet (tila, jossa kaikki voimat ovat tasapainossa) eivät kiihdytä.
Newtonin mukaan esine kiihtyy vain, jos siihen on netto tai epätasapainoinen voima. Epätasapainoisen voiman läsnäolo kiihdyttää esinettä muuttaen nopeuttaan, suuntaansa tai nopeuttaan ja suuntaan.
Newtonin toinen liikkeen laki
Tämä laki viittaa esineiden käyttäytymiseen, joihin kaikki nykyiset voimat eivät ole tasapainossa. Toisessa laissa todetaan, että esineen kiihtyvyys riippuu kahdesta muuttujasta: esineen esineeseen ja massaan käyttämästä nettovoimasta.
Objektin kiihtyvyys riippuu suoraan esineeseen vaikuttavasta nettovoimasta ja käänteisesti esineen massasta. Kun esineeseen vaikuttava voima kasvaa, esineen kiihtyvyys kasvaa.
Kohteen massan lisääntyessä esineen kiihtyvyys vähenee. Newtonin toinen liikkeen laki voidaan muodollisesti julistaa seuraavasti:
"Nettovoiman tuottaman esineen kiihtyvyys on suoraan verrannollinen nettovoiman suuruuteen, samaan suuntaan kuin nettovoima ja käänteisesti verrannollinen esineen massaan".
Tämä sanallinen lausunto voidaan ilmaista yhtälön muodossa seuraavasti:
A = fnet / m
Aikaisempi yhtälö on usein järjestetty tutumpaan tapaan, kuten alla on esitetty. Nettovoima rinnastetaan massan tuotetta kerrottuna kiihtyvyydellä.
Fnet = m • a
Voi palvella sinua: tilavuusvirtaPainopiste on aina nettovoimassa. Kiihtyvyys on suoraan verrannollinen nettovoimaan. Nettovoima on yhtä suuri kuin massa kerrottuna kiihtyvyydellä.
Kiihtyvyys samaan suuntaan kuin nettovoima, on nettovoiman tuottama kiihtyvyys. Se on kiihtyvyyteen liittyvä nettovoima, nettovoima on kaikkien voimien vektorisumma.
Jos kaikki yksittäiset voimat tunnetaan, jotka vaikuttavat esineeseen, nettovoima voidaan määrittää.
Edellisen yhtälön mukaan voimayksikkö on yhtä suuri kuin massayksikkö kerrottuna kiihtyvyysyksiköllä.
Korvaamalla standardi metriset yksiköt, massa ja kiihtyvyys edellisessä yhtälössä, voit kirjoittaa seuraavan yksikön vastaavuuden.
1 Newton = 1 kg • M / S2
Standardimetrisen yksikön määritelmä on merkitty edellisellä yhtälöllä. Newton määritellään voiman määräksi, joka vaaditaan 1 kg: n massan ja 1 m / s / s.
Ja yhtälö
Newtonin toisen lain mukaan, kun esine kiihtyy, silloin on oltava nettovoima, joka toimii. Päinvastoin, jos nettovoima vaikuttaa esineeseen, tämä esine kiihtyy.
Objektiin vaikuttavan nettovoiman suuruus on yhtä suuri kuin esineen massa kerrottuna kohteen kiihtyvyydellä seuraavassa kaavassa esitetyllä tavalla:
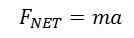
Verkkovoima on jäljellä oleva voima, joka tuottaa kaiken kohteen kiihtyvyyden, kun kaikki vastakkaiset voimat on peruutettu.
Vastakkaiset voimat vähentävät kiihtyvyyden vaikutusta vähentäen esineeseen vaikuttavan kiihtyvyyden nettovoimaa.
Jos esineeseen toimiva nettovoima on nolla, niin objektia ei kiihdytetä ja se on tilassa, jota kutsumme saldoksi.
Se voi palvella sinua: Ortonormal Base: Ominaisuudet, esimerkit ja harjoituksetKun esine on tasapainossa, niin kaksi asiaa voi olla totta: joko esine ei liiku ollenkaan tai esine liikkuu vakiona nopeudella. Tasapaino kaava on esitetty alla:
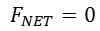
Esimerkit
Harkitse hypoteettista tilannetta avaruudessa. Teet avaruuskävelyä ja kiinnität jotain lauttasi. Työskentelemällä aiheeseen englannin avaimen kanssa, hän suuttuu ja heittää avaimen pois, mitä tapahtuu?
Kun avain poistuu kädestä, se jatkaa liikkumista samalla nopeudella, jonka se antoi sille, kun se heitti sen. Tämä on esimerkki tyhjästä voimatilanteesta. Avain liikkuu samalla nopeudella eikä kiihdytä avaruudessa.
Jos heität saman avaimen maahan, avain putoaa maahan ja lopulta pysähtyy. Miksi hän pysähtyi? Avaimessa on nettovoima, jolloin se hidastuu ja pysähtyy.
Toisessa esimerkissä sanotaan, että olet jäähalli. Ota jääkiekko -albumi ja liu'uta se jään läpi.
Lopulta jääkiekko -albumi hidastuu ja pysähtyy, jopa sileällä ja liukaslla jäällä. Tämä on toinen esimerkki tilanteesta, jolla on muu nettovoima kuin nolla.
Viitteet
- Fysiikan luokkahuone,. (2016). Newtonin toinen laki. 11-2-2017, fysiikasta.com -verkkosivusto: PhysicsClassroom.com.
- Cárdenas, r. (2014). Mikä on nettovoima? - Määritelmä, suuruus ja yhtälöt. 11-2-2017, osoitteesta http: // opiskelu.com -verkkosivusto: opiskelu.com.
- IAC Publishing, LLC. (2017). Mikä on nettovoima?. 11-2-2017, viitteestä.com -verkkosivusto: viite.com.
- Nettovoima. (n.d -d.) Websterin Reviso Unbrided Dictionary. (1913). Haettu 11. helmikuuta 2017 The Freedictionary.com.
- Pearson, a. (2008). Voima ja liike luku 5. Voima ja liike. 11-2-2017, kirjoittanut Pearson Education Inc -verkkosivusto: fysiikka.GSU.Edu.

