Mitä ovat coplanares -vektorit? (Ratkaistujen harjoitusten kanssa)

Se Coplanares -vektorit o Coplanarios ovat niitä, jotka sisältyvät samaan tasoon. Kun sinulla on vain kaksi vektoria, nämä ovat aina paria.

Jos sinulla on kolme tai useampia vektoreita, voi olla, että kuka tahansa heistä ei ole samassa tasossa kuin muut, siksi niitä ei voitu pitää koplaanina. Seuraava kuva näyttää joukon koplanareja, jotka on merkitty lihavoituina vektoreina -Lla, B -, C ja D -d-

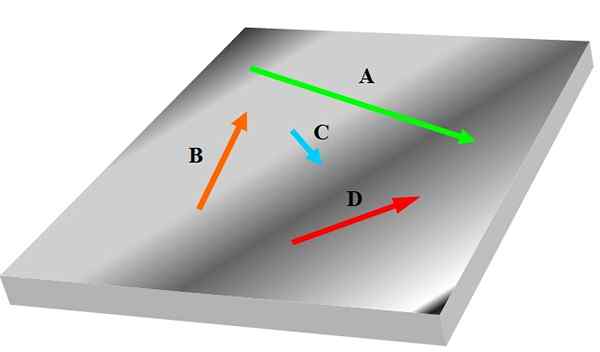Kuvio 1. Neljä coplanaresia. Lähde: Itse tehty.

Vektorit liittyvät tieteen ja tekniikan merkityksellisten fysikaalisten suuruuksien käyttäytymiseen ja ominaisuuksiin; Esimerkiksi nopeus, kiihtyvyys ja lujuus.

Voima tuottaa erilaisia ​​vaikutuksia objektiin, kun sen käyttötapa vaihtelee, esimerkiksi muuttaen intensiteettiä, suuntaa ja merkitystä. Yhden näiden parametrien muuttaminen edelleen tulokset ovat huomattavasti erilaisia.

Monissa sovelluksissa, sekä staattisessa että dynamiikassa, rungossa toimivat voimat ovat samalla tasolla, siksi niitä pidetään coplanaresina.

[TOC]

Olosuhteet, joiden vektorit ovat koplaaneja

Jotta kolme vektoria olisi koplanares, heidän on oltava samalla tasolla ja tämä tapahtuu, jos he täyttävät seuraavat ehdot:

-Vektorit ovat yhdensuuntaisia, joten niiden komponentit ovat suhteellisia ja ovat lineaarisesti riippuvaisia.

-Sekoitettu tuotteesi on tyhjä.

-Jos sinulla on kolme vektoria ja jokin niistä voidaan kirjoittaa kahden muun lineaarisena yhdistelmänä, nämä vektorit ovat coplanares. Esimerkiksi vektori, joka johtuu kahden muun summasta, kolme ovat samassa tasossa.

Voi palvella sinua: Voltimetri: Ominaisuudet, toiminta, mitä se on, tyypit

Vaihtoehtoisesti koplanarisuuden tila voidaan vahvistaa seuraavasti:

U v w Ne ovat koplanareja, jos on kolme numeroa (skalaaria) α, β, y siten, että αtai + βv + γW = 0 (Α, β, γ) erilainen kuin (0, 0, 0)

Sekoitettu tuote kolmen vektorin välillä

Vektoreiden välinen sekoitettu tuote määritetään kolmella vektorilla tai, v ja W -, Tuloksena on skalaari, joka johtuu seuraavan toiminnan suorittamisesta:

tai · (v x W -) = tai · (V x W --A

Ensinnäkin suluissa oleva ristituote on valmistettu: v x W -, jonka tulos on normaali (kohtisuora) vektori tasolle, jossa he ovat niin v kuten W -.

Joo tai on samalla tasolla kuin v ja W -, Luonnollisesti u: n ja mainitun normaalin vektorin välisen skalaarituotteen (pistetuote) on oltava 0. Tällä tavoin varmistetaan, että kolme vektoria ovat koplaaneja (ne sijaitsevat samalla tasolla).

Kun sekoitettu tuote ei ole nolla, sen tulos on yhtä suuri kuin rinnakkaiskipien tilavuus, jolla on vektorit tai, v ja W - viereisinä puolina.

Sovellukset

Koplanares, samanaikaiset ja ei -kolineaaliset joukot

Vahvuudet samanaikainen Ne kaikki levitetään samaan kohtaan. Jos ne ovat myös koplaaneja, ne voidaan korvata vain yhdellä, jota kutsutaan tuloksena oleva voima Ja sillä on sama vaikutus kuin alkuperäisten voimien.

Jos ruumis on tasapainossa kolmen koplanaarin, samanaikaisten ja ei -kolineaalisten (ei -parallelien) voimien ansiosta, nimeltään -Lla, B - ja C, hän Lamyn lause Hän huomauttaa, että näiden voimien (suuruudet) välinen suhde on seuraava:

A / sin α = b / SEN β = c / sen γ

Α: n, β: n ja y: n kanssa kulmana vastustavat sovellettuja voimia, kuten seuraavassa kuvassa esitetään:

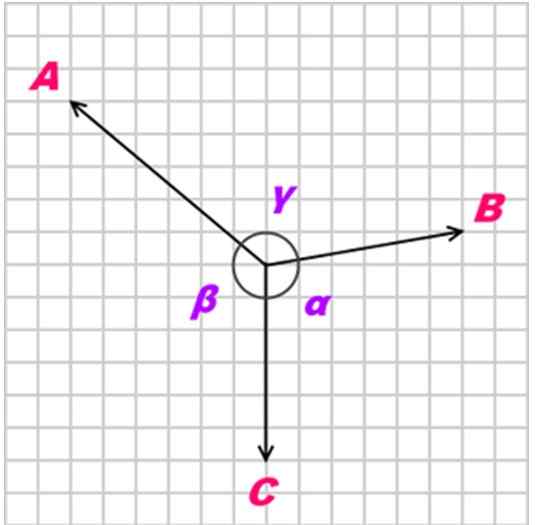Kuva 2. Kolme voimaa A, B ja C Coplanares toimivat esineeseen. Lähde: Kiwakwok English Wikipediassa [julkinen verkkotunnus]

Ratkaisut

-Harjoitus 1

Löydä K: n arvo niin, että seuraavat vektorit ovat koplanareja:

Voi palvella sinua: Carnot Machine

tai =

v =

W - =

Ratkaisu

Koska vektorien komponentit ovat olleet, sekoitettujen tuotteiden kriteerejä käytetään, siksi:

tai · (v x W -) = 0

Se on ratkaistu ensin v x W -. Vektorit ilmaistaan ​​yksikkövektoreina Yllyttää, J - ja k -k - Se erottaa kolme kohtisuoraa suuntaa avaruudessa (leveä, korkea ja syvyys):

v= 4 Yllyttää + J - + 0 - k -k -

W -= -1 Yllyttää + 2J - -1 k -k -

v x W = -4 (I x i) + 8 (i x j) - 4 (I x k) - (J X I) + 2 (J X J) - 2 (J X K) = 8 k -k - + 4 J + k -2 i = -2 Yllyttää + 4 J - + 9 k -k -

Skalaarituotetta ehdotetaan nyt U: n ja vektorin välillä, jolla on tulokset edellisestä toiminnasta, sovitusoperaatioon 0:

tai · (v x W -) = (-3 Yllyttää + k -k - J - + 2 k -k --A · (-2 Yllyttää + 4 J - + 9 k -k -) = 6 + 4K +18 = 0

24 + 4K = 0

Haettu arvo on: k = - 6

Niin että vektori tai On:

tai =

-Harjoittele 2

Kuvio näyttää objektin, jonka paino on w = 600 N, ripustettuna tasapainossa kuvassa 3 olevien kulmien mukaisten kaapeleiden ansiosta. Onko mahdollista soveltaa Lamyn lauseen tässä tilanteessa? Joka tapauksessa löydä suuruudet T₁, T₂ ja T₃ jotka tekevät tasapainon mahdolliseksi.

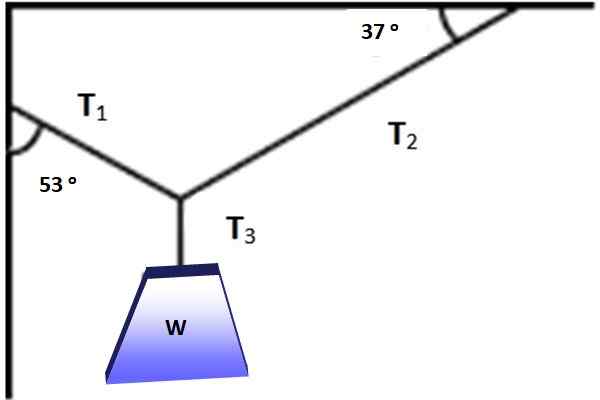Kuva 3. Paino roikkuu tasapainossa esitetyn kolmen jännitteen vaikutuksen alla. Lähde: Itse tehty.

Ratkaisu

Lamyn lause on sovellettavissa tässä tilanteessa, jos solmu, johon kolmea jännitteitä käytetään. Ensin tehdään vapaa kehon kaavio riipuksen painosta T: n suuruuden määrittämiseksi_3:

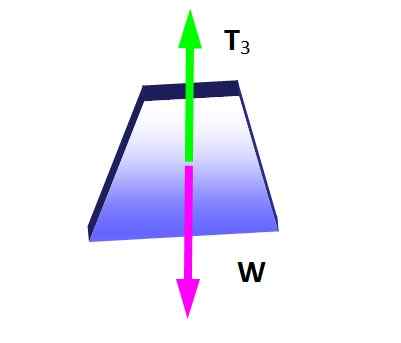Kuva 4. Ilmainen runkokaavio painon roikkuu. Lähde: Itse tehty.

Tasapainolosuhteista seuraa, että:

Voi palvella sinua: äänen diffraktio: Mikä on, esimerkkejä, sovelluksia

T₃  = W = 600 N

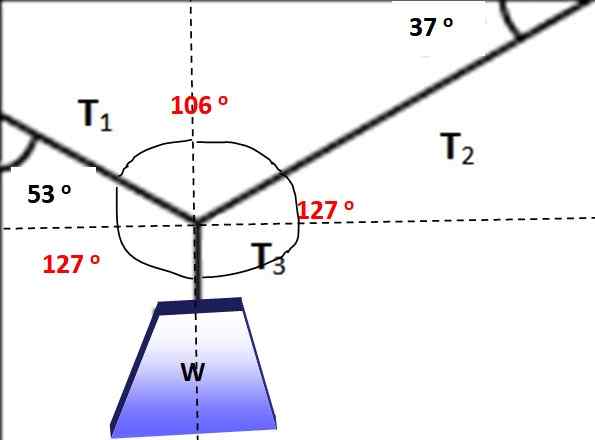
Voimien väliset kulmat on merkitty punaisella seuraavassa kuvassa, voidaan helposti varmistaa, että sen summa on 360 °. Nyt on mahdollista levittää Lamyn lause, koska yksi joukkoista ja niiden väliset kolme kulmaa tunnetaan:

Kuva 5.- Punaisessa kulmassa Lamyn lauseen levittämiseksi. Lähde: Itse tehty.

T₁ / Sen 127º = W / SEN 106º

Siksi: t₁ = Sen 127º (W /SEN 106º) = 498.5 n

Jälleen Lamyn lause levitetään selkeän t₂-

T₂ / sin 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 n

Viitteet

1. Figueroa, D. Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. 31-68.
2. Fyysinen. Moduuli 8: Vektorit. Toipunut: FRTL.Utn.Edu.AR
3. Hibbeler, R. 2006. Insinöörien mekaniikka. Staattinen. 6. painos. Mannertoimitusyhtiö.28-66.
4. McLean, W. Schaum -sarja. Insinöörien mekaniikka: staattinen ja dynaaminen. Kolmas painos. McGraw Hill. 1-15.
5. Wikipedia. Vektori. Palautettu: se on.Wikipedia.org.