Samankaltaisten termien vähentäminen

Mikä on samanlaisten termien vähentäminen?

Se Samankaltaisten termien vähentäminen Se on menetelmä, jota käytetään algebrallisten lausekkeiden yksinkertaistamiseen. Algebrallisessa ekspressiossa samanlaiset termit ovat ne, joilla on sama muuttuja; toisin sanoen heillä on samat tuntemattomat kirjaimet, ja heillä on samat eksponentit.

Joissakin tapauksissa polynomit ovat laajoja, ja saavuttaaksesi ratkaisun sinun on yritettävä vähentää ekspressiota; Se on mahdollista, kun on samanlaisia ​​termejä, jotka voidaan yhdistää soveltamalla algebrallisia operaatioita ja ominaisuuksia, kuten summa, vähennys, kertolasku ja jako.

Selitys

Samanlaiset termit muodostavat samat muuttujat samoilla eksponenteilla, ja joissain tapauksissa nämä eroavat vain niiden numeeristen kertoimien mukaan.

Niitä, joilla ei ole muuttujia, pidetään myös samanlaisina termeinä; eli ne termit, joilla on vain vakioita. Siten esimerkiksi seuraavat ovat samanlaisia ​​termejä:

• 6x² - 3x². Molemmilla termeillä on sama muuttuja x².
• Neljäs²b -³ + Toinen²b -³. Molemmilla termeillä on samat muuttujat²b -³.
• 7 - 6. Ehdot ovat vakioita.

Niitä termejä, joilla on samat muuttujat, mutta erilaisilla eksponenteilla kutsutaan ei -samanlaisia ​​termejä, kuten:

• Yhdeksäs²B + 5AB. Muuttujilla on erilaiset eksponentit.
• 5x + ja. Muuttujat ovat erilaisia.
• B - 8. Yksi termi on muuttuja, toinen on vakio.

Tunnistamalla samanlaiset termit, jotka muodostavat polynomin, nämä voidaan pelkistää yhdeksi yhdistämällä kaikki ne, joilla on samat muuttujat, joilla on yhtä suuret eksponentit. Tällä tavalla lauseketta yksinkertaistetaan vähentämällä sitä muodostavien termien lukumäärää ja sen ratkaisun laskemista helpotetaan.

Kuinka vähentää samanlaisia ​​termejä?

Samankaltaisten ehtojen vähentäminen tapahtuu soveltamalla tuotteen lisäys- ja jakautumisominaisuuden assosiatiivinen ominaisuus. Seuraavaa menettelyä käyttämällä voidaan vähentää termien vähentämistä:

• Ensinnäkin samanlaiset termit on ryhmitelty yhteen.
• Samankaltaisten termien kertoimet (luvut, jotka seuraavat muuttujia) lisätään tai vähennetään, ja tapauksen mukaan assosiatiivisia, kommutatiivisia tai jakautuvia ominaisuuksia sovelletaan.
• Sitten kirjoitetaan uudet ehdot, asettamalla heidän eteensä merkki, joka johtui operaatiosta.

Voi palvella sinua: Disretillinen matematiikka

Esimerkki

Vähennä seuraavan lausekkeen ehtoja: 10x + 3y + 4x + 5y.

Ratkaisu

Ensinnäkin ehdot on määrätty ryhmittelemään samankaltaiset, soveltamalla kommutatiivista omaisuutta:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Sitten levitetään jakautuvaa ominaisuutta ja muuttujia mukana olevat kertoimet lisätään termien vähentämisen saamiseksi:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) ja

= 14x + 8y.

Samankaltaisten ehtojen vähentämiseksi on tärkeää ottaa huomioon merkit, joilla on muuttujan mukana olevat kertoimet. Mahdollisia tapauksia on kolme:

Samankaltaisten termien vähentäminen yhtäläisillä merkkeillä

Tässä tapauksessa kertoimia lisätään ja tulosten edessä termien merkki on sijoitettu. Siksi, jos ne ovat positiivisia, tuloksena olevat termit ovat positiivisia; Jos termit ovat negatiivisia, tuloksella on merkki (-) muuttujan mukana. Esimerkiksi:

a) 22ab² + 12AB² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Samankaltaisten termien C vähentäminenEri merkkeillä

Tässä tapauksessa kertoimet vähennetään, ja tuloksen edessä pääkertoimen merkki asetetaan. Esimerkiksi:

a) 15x²ja - 4x²ja + 6x²ja - 11x²ja

= (15x²ja + 6x²Y) + ( - 4x²ja - 11x²ja)

= 21x²Y + (-15x²ja)

= 21x²ja - 15x²ja

= 6x²ja.

b) -5a³B + 3 a³B - 4a³b + a³b -

= (3 a³b + a³b) + (-5a³B - 4a³b)

= 4a³B - 9a³b -

= -5 a³b -.

Tällä tavoin samankaltaisten termien vähentämiseksi, joilla on erilaisia ​​merkkejä, muodostetaan yksi lisäaine, jolla on positiivinen merkki (+), kertoimet lisätään ja tulokseen liittyy muuttujia.

Se voi palvella: yhtenäinen ympyrä: trigonometriset toiminnot ja sovellukset

Samoin muodostetaan vähentävä termi, ja kaikilla termeillä, joilla on negatiivinen merkki (-), kertoimia lisätään ja tulokseen liittyy muuttujia.

Lopuksi kahden muodostetun termin summat vähennetään, ja suurimman merkki asetetaan tulokseen.

Samanlaisten termien vähentäminen toiminnassa

Samankaltaisten termien vähentäminen on algebra -operaatio, jota voidaan soveltaa yhteensä, vähennys-, kertolasku- ja algebrallinen jako.

Summissa

Kun sinulla on useita polynomeja, joilla on samanlaisia ​​termejä, niiden vähentämiseksi, kunkin polynomin ehdot määrätään pitämään merkkinsä, sitten ne on kirjoitettu muiden jälkeen ja samanlaiset termit vähenevät. Esimerkiksi, sinulla on seuraavat polynomit:

3x - 4xy + 7x²ja + 5xy².

- 6x²ja - 2xy + 9 xy² - 8x.

Vähennettynä

Polynomin vähentämiseksi toisesta, minuend kirjoitetaan ja vähentämällä sen sitten muuttuneilla merkkeillä, ja sitten vastaavien termien vähentäminen tehdään. Esimerkiksi:

Viides³ - 3AB² + 3b²c

6AB² + Toinen³ - 8b²c

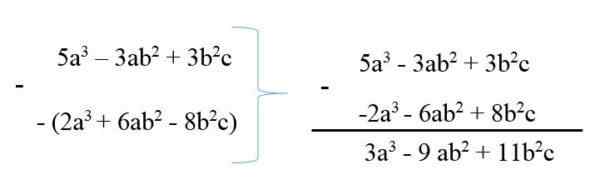
Siten polynomit on esitetty yhteenvetona 3A: ssa³ - 9AB² + 11b²c.

Kertolaskuina

Polynomituotteessa termit, jotka muodostavat kertomisen jokaiselle kerroimelle.

Ne vaihdetaan vain kertomalla negatiivisella termillä; Toisin sanoen, kun saman merkin kaksi termiä kertoo, tulos on positiivinen (+), ja kun niillä on erilaisia ​​merkkejä, tulos on negatiivinen (-).

Esimerkiksi:

a) (a + b) _* (A + B)

= a² + Ab + ab + b²

= a² + 2AB+ B².

b) (a + b) _* (A - b)

= a² - Ab + ab - b²

= a² - b -².

c) (a - b) _* (A - b)

= a² - AB - AB + B²

= a² - 2AB+ B².

Osastoissa

Kun haluat vähentää kahta polynomia jaon kautta, kolmas polynomin täytyy.

Se voi palvella sinua: Tukey -testi: Mikä on esimerkiksi ratkaistu harjoitus

Sitä varten osingon ja jakajan ehdot on tilata vasemmalta oikealle, niin että muuttujat molemmissa ovat samassa järjestyksessä.

Jako suoritetaan sitten osingon vasemmasta ensimmäisestä toimikaudesta ensimmäisen jakajan vasemmalla puolella, ottaen aina huomioon kunkin kauden merkit.

Vähennä esimerkiksi polynomi: 10x⁴ - 48x³ja + 51x²ja² + 4xy³ - 15y⁴ jakamalla se polynomin välillä: -5x² + 4xy + 3y².

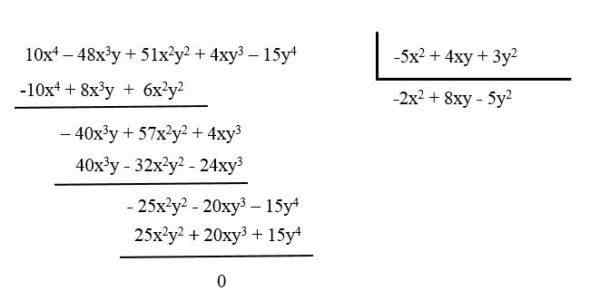
Tuloksena oleva polynomi on -2x² + 8xy - 5y².

Ratkaisut

Ensimmäinen harjoitus

Vähennä annetun algebrallisen ekspression ehtoja:

15a² - 8ab + 6a² - 6AB - 9 +4a² - 13 AB.

Ratkaisu

Summummutatiivista ominaisuutta sovelletaan, ryhmittelemällä termit, joilla on samat muuttujat:

15a² - 8ab + 6a² - 6AB + 9 + 4A² - 13

= (15a² + Kuudes² + Neljäs²) + ( - 8ab - 6ab) + (9 - 13).

Sitten käytettiin kertolaskun jakautuvaa ominaisuutta:

15a² - 8ab + 6a² - 6AB + 9 + 4A² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Lopuksi niitä yksinkertaistetaan lisäämällä ja vähentämällä kunkin termin kertoimet:

15a² - 8ab + 6a² - 6AB + 9 + 4A² - 13

= 25a² - 14ab - 4.

Toinen harjoitus

Yksinkertaista seuraavien polynomien tuotetta:

(8x³ + 7xy²-A_*(8x³ - 7 XY²-A.

Ratkaisu

Jokainen ensimmäisen polynomin termi kerrotaan toisella, ottaen huomioon, että termien merkit ovat erilaisia; Siksi sen kertolasku on negatiivinen, samoin kuin eksponenttien lakeja on sovellettava.

(8x³ + 7xy²-A _* (8x³ - 7xy²-A

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²ja⁴

= 64 x⁶ - 49 x²ja⁴.