Funktion kirjeenvaihtosääntö

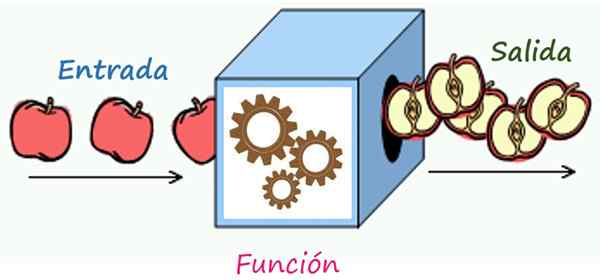
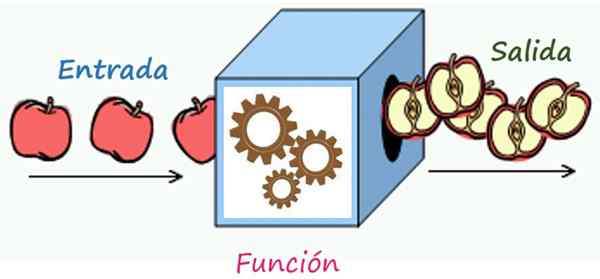Kirjeenvaihtosääntö on mekanismi, joka muuttaa lähtöelementteihin pääsyn elementit. Lähde: Wikimedia Commons/F. Zapata

Mikä on funktion kirjeenvaihtosääntö?

Se funktion kirjeenvaihtosääntö Huomauttaa tapa, jolla yhden sarjan elementit liittyvät toisen elementteihin. Ensimmäisen sarjan elementit tunnetaan nimellä verkkotunnus, ja toisen, kuten Kodomini jompikumpi ristiriita.

Suhde tai linkki joukkojen välillä voidaan määrittää sanallisella tai kirjallisella käskyllä, mutta kun sarjat ovat numeerisia, kirjeenvaihtosääntö on merkitty kaavalla.

Tämä kaava sisältää operaatiot, jotka on tehtävä aloituskokoonpanon elementeillä, ja siten hankkia sarja elementtejä, jotka sisältyvät Codominiumiin.

Nyt kun elementtien välinen suhde on funktio, kirjeenvaihtosääntö täyttää kaksi erityistä ehtoa:

• Jokaiselle domeenin elementille liittyy kirjeenvaihtosäännön kautta Codominiumin yksittäiseen elementtiin, joka tunnetaan nimellä kuva.
• Tämä kuva on ainutlaatuinen, toisin sanoen, mikään verkkotunnuksen elementti ei liity useampaan kuin yhteen kodominiumin elementtiin.

Tällä tavoin voit kuvitella funktion kirjeenvaihtosäännön laatikkoon lukittuna mekanismina. Jokainen verkkotunnusarvo, poikkeuksetta, voi kirjoittaa laatikko ja päästä pois siitä, että se on transformoitu, kirjeenvaihtosäännön osoittamien toimintojen kautta. Esimerkit nähdään heti.

Esimerkit

Esimerkki 1

Funktion kirjeenvaihtosääntö voidaan ilmaista kirjallisena ohjeena, kun elementit eivät ole numeerisia.

Esimerkiksi siellä on joukko maita, jotka on merkitty P: ksi ja toinen joukko kaupunkeja C:

Se voi palvella sinua: u -testi Mann - Whitney: Mikä se on ja sovellettaessa, suoritus, esimerkki

P = Kanada, Meksiko, Espanja, USA, Ranska, Argentiina, Brasilia, Saksa

C = Pariisi, Lontoo, Buenos Aires, Berliini, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rooma, Brasilia, Toronto

Olla kirjeenvaihtosääntö F P: n ja C: n välillä:

F: P → c

Missä F Se on sääntö "... Kenen pääoma on .. ”, Joka yhdistää jokaisen maan P: ssä (aloitusjoukko), pääkaupunki C (saapumisjoukko).

Esimerkiksi: ”Espanja, Kenen pääoma on Madrid ". "Espanja" -elementti kuuluu käynnistysjoukkoon ja "Madrid" -elementtiin koko C: lle, saapuminen.

Tämän funktion esitys voidaan tehdä Venn -kaavion kautta tai yksinkertaisesti tilattujen parien kautta.

Tilatut parit sisältävät, kuten nimestä voi päätellä, kaksi elementtiä, joilla on tietyssä järjestyksessä, parin ensimmäinen elementti on maa ja toinen, sen pääkaupunki.

Venn -kaavio puolestaan ​​on tapa visualisoida funktio, joka näyttää lähtö- ja saapumisjoukot, samoin kuin heidän välilläan oleva kirjeenvaihtosääntö.

F: n esitys tilatuina pareina

F = (Kanada, Ottawa); (Meksiko, Mexico City); (Espanja Madrid); (USA; Washington); (Pariisi, Ranska); (Argentiina Buenos Aires); (Brasilian brasilia); (Saksa, Berliini)

Ensimmäinen pari yhdistää Kanadan, Kenen pääoma on Ottawa, toinen osakkuusyhtiö Meksiko, Kenen pääoma on Meksikon kaupunki ja niin edelleen.

F: n esitys Venn -kaaviona

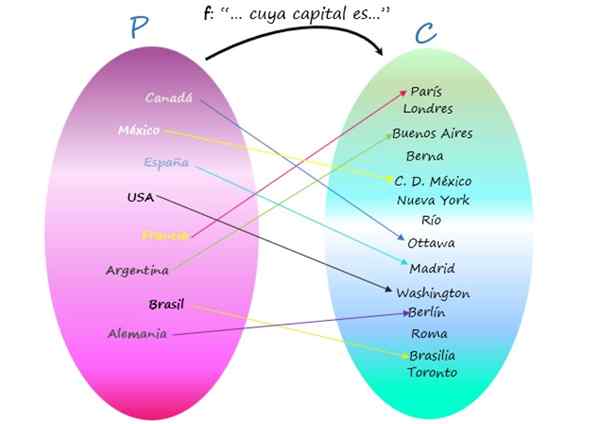
Huomaa, että on kaupunkeja, jotka eivät ole minkään maan pääkaupunkia, koska vaikka ne ovat kodominiumin elementtejä, ne eivät ole kuva minkään aloitusjoukon elementtiä. Silti suhde on tehtävä, koska tärkeätä on, että jokaisella maalla on pääoma, ja tämä on ainutlaatuinen.

Voi palvella sinua: tavallisen ja epäsäännöllisen Pentagonin alue: miten se otetaan, harjoitukset

Codominiumin elementtien muodostamaa alajoukkoa, jotka ovat kuvan jonkin verran domeenin elementtiä, kutsutaan funktion alue tai funktio. Esimerkiksi reitti r F On:

R = Pariisi, Buenos Aires, Meksiko City, Ottawa, Madrid, Berliini, Washington, Brasilia

On syytä kysyä, voidaanko C: n ja P: n välinen suhde, missä C: stä tulee aloitusjoukko ja saapuminen. Vastaus on kyllä, mutta se ei olisi funktio, koska on kaupunkeja, jotka eivät ole pääkaupunkeja, kuten New York tai maa, jonka pääkaupunki ei ole P -kompleksin, kuten Rooma, keskuudessa, kuten Rooma.

Esimerkki 2

Kun lähtöjoukko ja saapumisjoukko ovat numeerisia, ne linkittävän funktion vastaavuuden sääntö on kaava. Ole esimerkiksi toiminnon hallitseminen seuraava sarja:

D = 0, 1, 2, 3, 4, 5, 6)

Kirjeenvaihtosääntö F: D → R, joka linkittää D: n elementit reaaliluvut r on:

F: "Kaksinkertainen"

Jos ”X” on aloitusjoukon elementti, F (x) on vastaava saapumisjoukon elementti ja kirjeenvaihtosääntö on kirjoitettu kuten:

f (x) = 2x

Codominium on reaalilukujen joukko. Reain osajoukko on tämän toiminnon reitti, numerosarja, jonka arvo on kaksi kertaa x:

R = 0, 2, 4, 6, 8, 10, 12

Tilattujen parien muodossa kirjeenvaihtosääntö johtaa:

F = (0,0); (1,2); (2,4); (3,6); (4,8); (5.10); (6,12)

Tilatut parit voivat olla kuvaaja Cartesian lentokoneessa. Vääntömomentin ensimmäinen elementti asetetaan vaakasuoraan akseliin, jota kutsutaan myös abscissas- tai "x" -akseliksi, kun taas toinen menee järjestetyn tai yksinkertaisesti akselin pystysuuntaisella akselilla, "y":

Voi palvella sinua: jakava omaisuus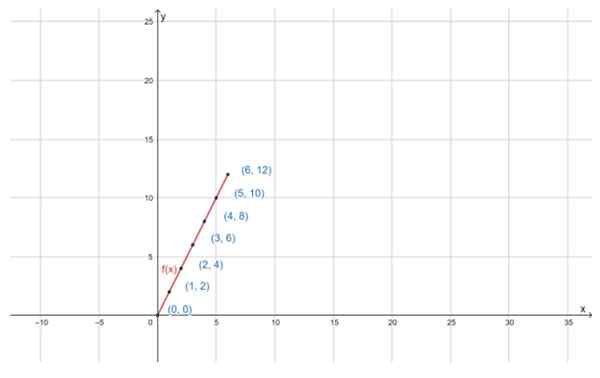 Funktion f (x) = 2x kuvaaja määritettyyn D -domeeniin on suora viiva. Lähde: f. Zapata Geogebran kautta

Harjoitukset

Määritä seuraavien suhteiden kirjeenvaihtosääntö osoittaen, ovatko ne toimintoja vai eivät. Luonnollisten lukujen joukko on n ja todellisen on r.

Ilmoita myös domeeni, codominium ja funktion reitti tapauksissa, joissa se vastaa:

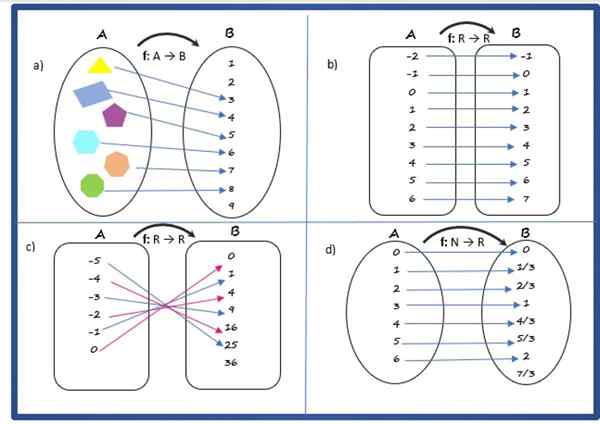
Liittää jhk

Se on funktio, koska jokaisella aloitusjoukon elementillä, joka koostuu monikulmioista, on ainutlaatuinen kuva saapumisjoukossa.

Kirjeenvaihtosääntö yhdistää monikulmion sen sivujen lukumäärään, domeeni koostuu monikulmioiden sarjasta:

A = kolmio, nelikulmainen, pentagon, kuusikulmainen, heptagon, kahdeksankulma

Codominium on sarja ensimmäisiä luonnollisia lukuja, mukaan lukien 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Ja Co C ovat luonnollisia lukuja välillä 3 - 8:

C = 3, 4, 5, 6, 7, 8

Ratkaisu b

Se on funktio, koska se täyttää edellä mainitut ehdot.

Kirjeenvaihtosääntö on:

f (x) = x + 1

Kirjeenvaihtosääntö osoittaa, että funktio on määritelty r → r, siksi verkkotunnus on reaalilukujen joukko. Ja co -oominium ja reitti osuvat myös todellisen kanssa.

Liuos C

Se on funktio, jossa on kirjeenvaihtosääntö:

f (x) = x²

Verkkotunnus ja kodominium on asetettu reagoihin, mutta reitti koostuu vain positiivisista reaalilukuista, merkittynä r⁺ ja mukaan lukien 0.

Liuos D

Se on funktio. Sen kirjeenvaihtosääntö on:

f (x) = x/3

Sen verkkotunnus on luonnonlukujen n ja codominium, samoin kuin reitti, ovat todelliset N -numerot r.