Sarrus -sääntö

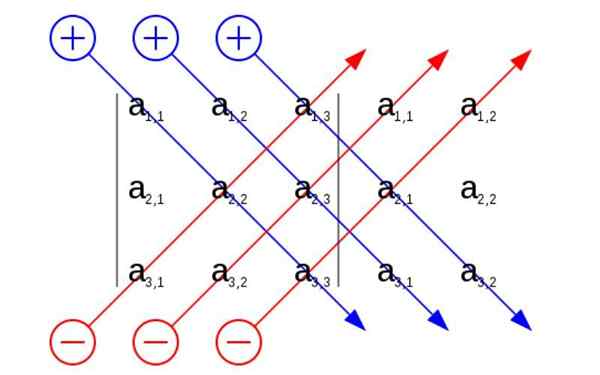
Sarrus -sääntö. Lähde: Käyttäjä: Sevela.P, CC BY-SA 4.0, Wikimedia Commons

Mikä on Sarruksen sääntö?

Se Sarrus -sääntö Se on tekniikka laskemaan neliömatriisin määrittäjät, jotka ovat vähintään 3 × 3. Tämä järjestelmä mahdollistaa ratkaisun helpommin. Sitä käytetään myös määrittämään, ovatko vektorisarjat lineaarisesti riippumattomia ja muodostavat vektoritilan pohjan.

Nämä sovellukset perustuvat matriisien kääntämiseen. Jos matriisi on säännöllinen, sen determinantti on erilainen kuin 0. Jos se on yksittäinen, sen determinantti on arvon arvoinen. Determinantit voidaan laskea vain neliömatriisien kanssa.

Minkä tahansa järjestyksen matriisien laskemiseksi Laplace -lausetta voidaan käyttää. Tämä lause antaa meille mahdollisuuden yksinkertaistaa korkeiden mittojen matriiseja pienten determinanttien summissa, jotka hajoamme päämatriisista.

Toteaa, että matriisin determinantti on yhtä suuri kuin kunkin rivin tai pylvään tuotteiden summa, sen kiinnitetyn matriisin determinantin avulla.

Tämä vähentää determinantteja, niin että n-1: n määräävästä määräävästä määrästä N-1. Jos soveltamme tätä sääntöä peräkkäisellä tavalla, voimme saada mitat 2 (2 × 2) tai 3 (3 × 3), jossa sen laskenta on paljon helpompaa.

Sarrus -sääntö

Pierre Frederic Sarrus (1798-1861) oli ranskalainen matemaatikko. Suurin osa sen matemaattisista sopimuksista perustuu yhtälöiden resoluutiomenetelmiin ja muunnelmien laskemiseen numeerisissa yhtälöissä.

Yhdessä sopimuksessaan hän ratkaisi yhden mekaniikan monimutkaisimmista arvoituksista. Nivelten kappaleiden ongelmien ratkaisemiseksi Sarrus esitteli vaihtoehtoisten suoraviivaisten liikkeiden muutoksen yhtenäisissä pyöreissä liikkeissä. Tämä uusi järjestelmä tunnetaan nimellä Sarrus -mekanismi.

Se voi palvella sinua: kustannusten ulkoistaminen ja internalisointi

Tutkimus, joka antoi hänelle eniten, oli se, jossa hän esitteli uuden menetelmän määrittävien tekijöiden laskemiseksi artikkelissa ”Nouvelles -menetelmät kaatavat la résolution des équations” (“Uusi menetelmä yhtälöiden ratkaisemiseksi”), joka on julkaistu vuonna 1833. Tämä tapa ratkaista lineaariset yhtälöt tunnetaan nimellä Sarrus -sääntö.

Sarrus -sääntö sallii laskea 3 × 3 -matriisin determinantin käyttämättä Laplacen lausetta, ottaen käyttöön paljon yksinkertaisemman ja intuitiivisemman menetelmän. 

Jotta voimme tarkistaa Sarrus -säännön arvon, otamme mitata 3:

Sen determinantin laskenta tehdään sen pää diagonaalien tuotetta, vähentämällä tuote käänteisistä diagonaaleista. Tämä olisi seuraava:

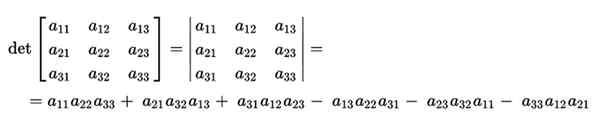
Sarrus -sääntö antaa meille mahdollisuuden saada paljon yksinkertaisempi visio laskettaessa determinantin diagonaaleja. Sitä yksinkertaistetaan lisäämällä kaksi ensimmäistä sarakketta matriisin takaosaan.

Tällä tavoin on selkeämpää sen tärkeimmistä diagonaaleista ja joka käänteinen tuotteen laskemiseksi.

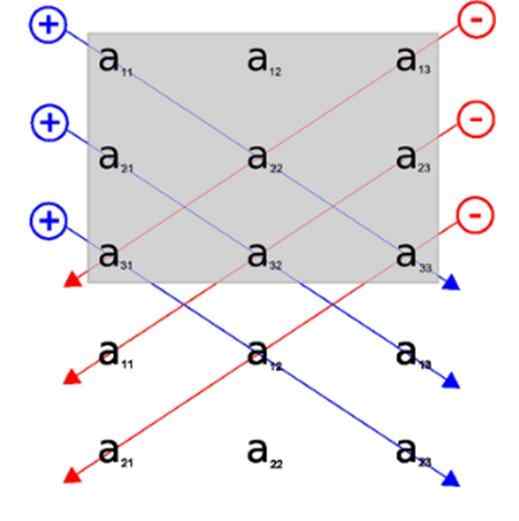
Tämän kuvan kautta voimme nähdä Sarrus -säännön soveltamisen, sisällytämme rivi 1 ja 2 alkuperäisen matriisin graafiseen esitykseen. Tällä tavoin tärkeimmät diagonaalit ovat kolme diagonaalia, jotka ilmestyvät ensisijaisesti.

Kolme käänteistä diagonaalia puolestaan ​​ovat ne, jotka ilmestyvät ensin takana.

Tällä tavoin diagonaalit ilmestyvät visuaalisemmalla tavalla, monimutkaismatta determinantin resoluutiota yrittäen selvittää, mitkä matriisin elementit kuuluvat jokaiseen diagonaaliin.

Voi palvella sinua: Quechua -sanat käännetään espanjaksi

Kuten kuvassa näkyy, valitsemme diagonaalit ja laskemme jokaisesta toiminnosta johtuvan tuotteen. Sinisinä ilmestyvät diagonaalit ovat ne, jotka lisäävät. Näiden summan mukaan vähennämme punaisella näkyvien diagonaalien arvon.

Jotta pakkaus olisi helpompaa, voimme käyttää numeerista esimerkkiä sen sijaan, että käyttäisimme algebrallisia termejä ja ala -termejä.

Jos otamme esimerkiksi 3 × 3 -matriisia:

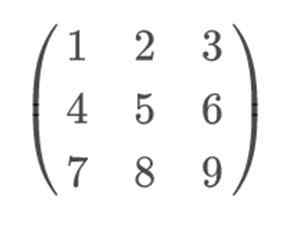
Sarrus -säännön soveltamiseksi ja sen ratkaisemiseksi visuaalisella tavalla meidän tulisi sisällyttää rivi 1 ja 2, kuten rivi 4 ja 5. On tärkeää ylläpitää riviä 1 4. sijalla ja rivi 2 viidennessä. Koska jos vaihdamme niitä, Sarrus -sääntö ei ole tehokas.

Matriisimme laskemiseksi matriisimme olisi seuraava:

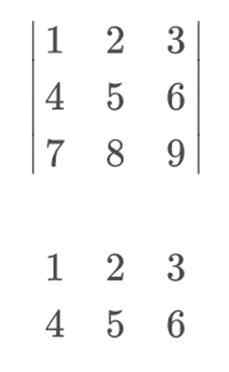
Laskennan jatkamiseksi kerrotaan pää diagonaalien elementit. Laskeutumalla, että he alkavat vasemmalla, on positiivinen merkki, kun taas käänteiset diagonaalit, jotka alkavat oikealta, kantavat negatiivisen merkin.

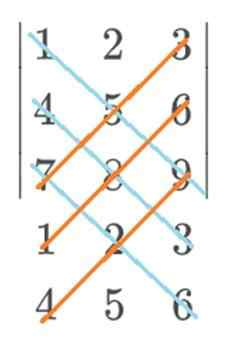
Tässä esimerkissä sininen menisi positiivisen merkin ja punaisen kanssa negatiivisella merkkillä. Sarrus -säännön lopullinen laskelma pysyy tällä tavalla:

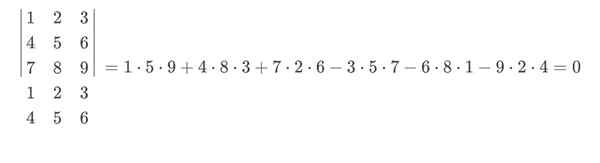
Kaverit tekijöiden

Mitan määrittäjä 1

Jos matriisin ulottuvuus on 1, matriisi on tällä tavalla: a = (a)

Siksi sen determinantti olisi seuraava: det (a) = | a | = a

Yhteenvetona matriisin A determinantti on yhtä suuri kuin matriisin A absoluuttinen arvo, joka tässä tapauksessa on A.

Mitta determinantti 2

Jos siirrymme Mitansion 2 matriiseihin, saadaan tyyppimatriisit:

Voi palvella sinua: Taumaattinen

Missä sen determinantti määritellään:

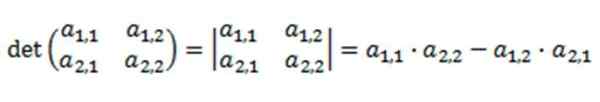
Tämän determinantin resoluutio perustuu sen tärkeimmän diagonaalin kertomiseen, vähentäen sen käänteisen diagonaalin tuotteen.

Mitta 3

Jos matriisin ulottuvuus on 3, tuloksena oleva matriisi olisi tämän tyyppistä:

Tämän matriisin määräävä tekijä ratkaistaan ​​tällä tavalla Sarrus -säännön kautta:

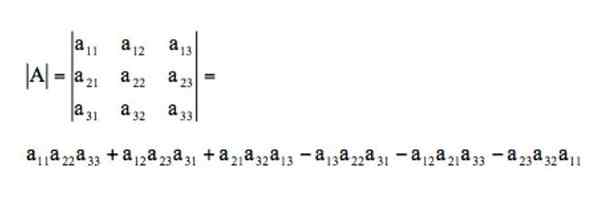
Viitteet

1. Anthony Nicolaides (1994). Determinantit ja matriisit. Pass -julkaisu.
2. M. Casteleiro Villalba (2004). Johdanto lineaariseen algebraan. ESIC -toimitus.