Ortonormal perusominaisuudet, esimerkit ja harjoitukset

Eräs Ortonormal -pohja Se on muodostettu kohtisuorilla vektoreilla toistensa kanssa ja jonka moduuli on myös 1 (yksikkövektorit). Muista, että pohja B - vektoritilassa V, Se on määritelty joukko lineaarisesti riippumattomia vektoreita, jotka kykenevät tuottamaan tämän tilan.

Vektoritila puolestaan ​​on abstrakti matemaattinen kokonaisuus, jonka elementtien välillä on vektoreita, jotka yleensä liittyvät fyysisiin suuruuksiin, kuten nopeuteen, lujuuteen ja siirtymiseen tai myös matriisien, polynomien ja toimintojen kanssa.

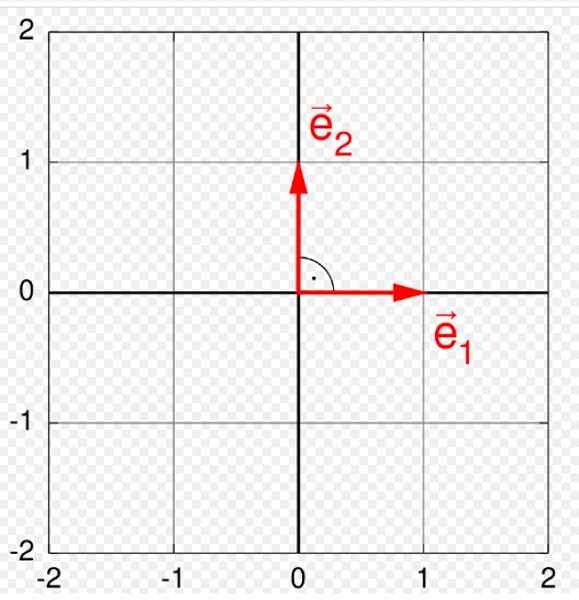
Kuvio 1. Ortonormaali pohja koneessa. Lähde: Wikimedia Commons. Quartl [CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Vektoreilla on kolme erottuvaa elementtiä: suuruus tai moduuli, suunta ja merkitys. Ortonormal -pohja on erityisen hyödyllinen edustamaan ja toimimaan heidän kanssaan, koska kaikki vektori, joka kuuluu tiettyyn vektoritilaan V, Se voidaan kirjoittaa vektorien lineaarisena yhdistelmänä, jotka muodostavat ortonormal -pohjan.

Tällä tavoin vektorien, kuten summan, vähennysten ja mainitussa tilassa määriteltyjen tuotteiden väliset toiminnot analysoidaan analyyttisesti.

Fysiikan eniten käytettyjä emäksiä on yksikkövektorien muodostama pohja Yllyttää, J - ja k -k - edustavat kolmen dimensioisen tilan kolmea erottuvaa suuntaa: korkea, leveä ja syvyys. Nämä vektorit tunnetaan myös nimellä Yhtenäiset kanoniset vektorit.

Jos sen sijaan vektorit työskentelevät lentokoneessa, se riittää kahdella näistä kolmesta komponentista, kun taas vain yksi.

[TOC]

Perusominaisuudet

1- pohja B - Se on pienin mahdollinen vektorisarja, joka tuottaa vektoritilan V.

2- elementit B - He ovat lineaarisesti riippumattomia.

3- Mikä tahansa tukikohta B - vektoritilasta V, mahdollistaa kaikkien vektorien ilmaisemisen V Lineaarisena yhdistelmänä ja tämä muoto on ainutlaatuinen jokaiselle vektorille. Siksi a B - Se tunnetaan myös nimellä Generaattorijärjestelmä.

4- Sama vektoritila V voi olla erilaisia ​​emäksiä.

Voi palvella sinua: Keskipakovoima: Kaavat, miten se lasketaan, esimerkkejä, harjoituksia

Esimerkkejä tukikohdista

Alla useita esimerkkejä ortonormaalisista emäksistä ja yleensä emäksistä:

Kanoninen pohja ℜ ⁿ

Kutsutaan myös luonnonpohjaksi tai tavanomaiseksi pohjaksi ℜ ⁿ, Missä ℜ ⁿ Se on tilaa neitsyt, Esimerkiksi kolmiulotteinen tila on ℜ ³. Arvoksi n Sitä kutsutaan ulottuvuus vektoritilasta ja merkitsee Dim (v).

Kaikki vektorit, jotka kuuluvat ℜ ⁿ Niitä edustaa N-USA Tilattu. Avaruudelle ℜⁿ, Kanoninen tukikohta on:

ja₁ =; ja₂ =; ja_n =

Tässä esimerkissä olemme käyttäneet merkintää kiinnikkeillä tai ”suluilla” ja rohkeaksi yksikkövektoreille ja₁, ja₂, ja₃..

Kanoninen pohja ℜ³

Perhevektorit Yllyttää, J - ja k -k - He myöntävät saman esityksen ja riittävät kolmelle edustamaan vektoreita ℜ ³-

Yllyttää =; J - =;  k -k - =

Se tarkoittaa, että pohja voidaan ilmaista seuraavasti:

B = ; ;

Varmistaakseen, että he ovat lineaarisesti riippumattomia, heidän kanssaan muodostettu determinantti on ei -nolla ja myös 1: 1:

Kaikki vektorit, jotka kuuluvat ℜ, on myös oltava mahdollista kirjoittaa ³ Lineaarisena yhdistelmänä. Esimerkiksi voima, jonka suorakaiteen muotoiset komponentit ovat f_x = 4 n, f_ja = -7 N ja F_{z -z}= 0 N kirjoitetaan vektorimuodossa seuraavasti:

F = N = 4Yllyttää -7J - + 0 -k -k - N.

Siksi Yllyttää, J - ja k -k - muodosta ℜ generaattorijärjestelmä ³.

Muut ortonormalit ℜ³

Edellisessä osassa kuvattu standardipohja ei ole ainoa ortonormal perusta ℜ: ssä³. Täällä meillä on esimerkiksi perusta:

B -₁ = ; ;

B -₂ = ; ;

Voidaan osoittaa, että nämä emäkset ovat ortonormaaleja, sillä tämä muistamme olosuhteet, jotka on täytettävä:

Voi palvella sinua: aaltoileva optiikka

-Perustan muodostavien vektorien on oltava ortogonaalisia toisiinsa.

-Jokaisen heistä on oltava yhtenäistä.

Voimme tarkistaa sen tietäen, että heidän muodostamansa determinantin on oltava ei -nolla ja yhtä suuri kuin 1.

Pohja B₁ Se on juuri sylinterimäisten koordinaattien ρ, φ ja z, toinen tapa ilmaista vektoreita avaruudessa.

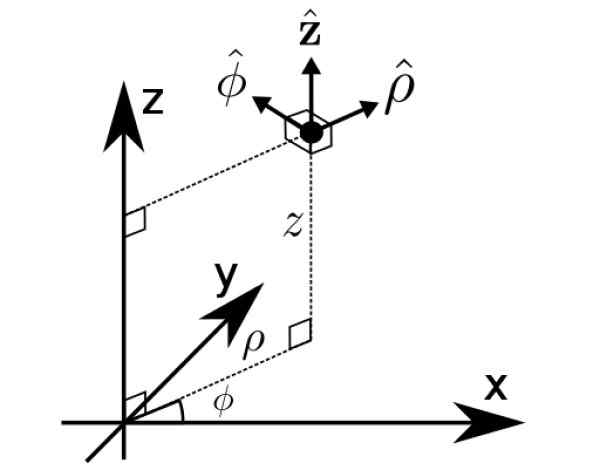Kuva 2. Lieriömäiset koordinaatit. Lähde: Wikimedia Commons. Matematiikan buff [CC BY-S (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Ratkaisut

- Harjoitus 1

Osoita, että pohja b = ; ; on ortonormal.

Ratkaisu

Osoittaaksemme, että vektorit ovat kohtisuorassa toisiinsa nähden, käytämme skalaarituotetta, jota kutsutaan myös kahden vektorin sisäiseksi tai tuotepisteeksi.

Anna kaikkien kahden vektorin tai ja v, Skalaarituotteesi on määritelty:

tai Olla v = tai.v. cosθ

Vektorit erottamiseksi heidän moduuleistaan ​​käytämme lihavoituna ensimmäisiin ja normaaleihin kirjaimiin jälkimmäiselle. θ on kulma tai ja v, Siksi, jos ne ovat kohtisuorassa, se tarkoittaa, että θ = 90º ja skalaarituote on tyhjä.

Vaihtoehtoisesti, jos vektorit annetaan niiden komponenttien suhteen: tai = x, tai_ja,tai_{z -z} > ja v = x, v_ja,v_{z -z} >, molempien skalaarituote, joka on kommutatiivinen, lasketaan tällä tavalla:

tai Olla v = tai_x .v_x + tai_ja .v_ja + tai_{z -z} .v_{z -z}

Tällä tavalla skalaarituotteet kunkin vektoriparin välillä ovat vastaavasti:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Toisessa tilassa lasketaan kunkin vektorin moduuli, joka saadaan:

│U │ = √ (u_x² + tai_ja² + tai_{z -z}²-A

Siten kunkin vektorin moduulit ovat:

│ = √ [(3/5)² + (4/5)²  + 0 -²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0 -²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Se voi palvella sinua: Toinen tasapainotila: Selitys, esimerkit, harjoitukset

│ = √ [0² + 0 -²  + 1²)] = 1

Siksi kolme ovat yksikkövektoreita. Lopuksi niiden muodostama determinantti ei ole nolla ja yhtä suuri kuin 1:

- Harjoitus 2

Kirjoita vektorikoordinaatit W - = Edellisen tukikohdan suhteen.

Ratkaisu

Tätä varten käytetään seuraavaa lausetta:

Olkoon b = v₁, v₂, v₃,.. v_n Ortonormaali pohja avaruudessa V kotimaisen tuotteen, vektorin kanssa W - Sitä edustaa B seuraavasti:

W - = <W -Ollav₁- v₁ + <W -Ollav₂- v₂ +<W -Ollav₃- v₃ +.. <W -Ollav_n- v_n

Tämä tarkoittaa, että voimme kirjoittaa vektorin B -pohjassa B kertoimien kautta <W -Ollav₁-, <W -Ollav₂>, ..  <W -Ollav_n>, jolle sinun on laskettava ilmoitetut skalaarit:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Saatujen skalaarituotteiden kanssa rakennetaan matriisi, nimeltään koordinaattimatriisi w.

Siksi vektorikoordinaatit W - Base B -BASE: ssä ne ilmaistaan:

[[W --_{B -}= [[(18/5); (1/5); 1-

Koordinaattimatriisi ei ole vektori, koska vektori ei ole sama kuin sen koordinaatit. Nämä ovat vain joukko numeroita, jotka ilmaisevat vektorin tietyllä pohjalla, ei vektoria sellaisenaan. Ne riippuvat myös valitusta pohjasta.

Lopuksi lauseen jälkeen, vektori W - ilmaistaan ​​seuraavasti:

W = (18/5) v₁ + (1/5) v₂ + v₃

Kanssa: v₁ =; v₂ =; v₃ =, Eli perusvektorit B -.

Viitteet

1. Larson, r. Lineaarisen algebran perusteet. Kuudes. Painos. Cengage -oppiminen.
2. Larson, r. 2006. Laskeminen. Seitsemäs. Painos. Nide 2. McGraw Hill.
3. Salas, J. lineaarialgebra. Aihe 10. Ortonormal tukikohdat. Palautettu: OCW.UC3M.On.
4. Sevillan yliopisto. Lieriömäiset koordinaatit. Vektoripohja. Toipunut: Laplace.meille.On.
5. Wikipedia. Ortonormal -pohja. Palautettu: on.Wikipedia.org.