Hypotoniset ratkaisukomponentit, valmistelu, esimerkit

Eräs Hypotoninen ratkaisu Se esittelee vähäisen liuenneen aineen pitoisuuden suhteessa liuokseen, joka on erotettu tai eristetty puolivälissä olevalla vikalla. Tämä este sallii liuottimen transeen, veden biologisten järjestelmien tapauksessa, mutta kaikki liuenneen hiukkaset eivät.

Solunsisäisten ja solunulkoisten selkärankaisten kehon nesteiden osmolaarisuus on noin 300 mOSm/l. Vaikka hypotonisen nesteen katsotaan olevan osmolaarisuus alle 280 mOSM/l. Joten tämän osmolaarisuuden ratkaisu on hypotoninen suhteessa soluväliaineeseen.

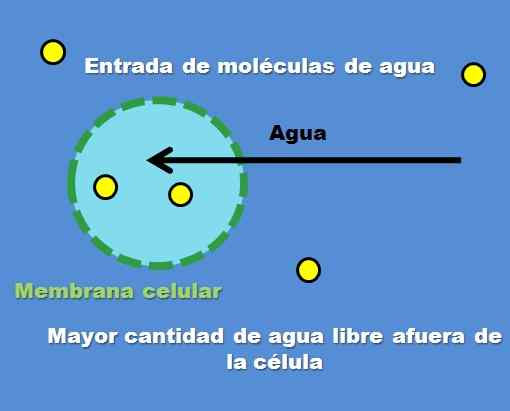
Solun vuorovaikutus hypotonisella liuoksella. Lähde: Gabriel Bolívar.

Esimerkki hypotonisesta liuoksesta on 0,45% natriumkloridia. Mutta miten solu tai osasto käyttäytyy tämän tyyppisen liuoksen edessä? Ylivoimainen kuva vastaa tähän kysymykseen.

Liuenneiden hiukkasten pitoisuus (keltaiset pisteet) on korkeampi ulkokennossa. Koska solun ympärillä on vähemmän liuennettua, vapaata vesimolekyylejä on enemmän, joten sitä esitetään voimakkaammalla sinisellä värillä verrattuna solun sisäpuolelle.

Vesi virtaa ulospäin osmoosin kautta tasopitoisuuksiin. Seurauksena solu laajenee tai tuuletin absorboimalla vettä, joka ylittää sen solukalvon.

[TOC]

Hypotonisten ratkaisujen komponentit

Hypotoniset liuokset koostuvat liuottimesta, joka, ellei toisin ilmoiteta, koostuu vedestä ja liuennut siihen liuenneena, kuten suolat, sokerit jne., puhdas tai sekoitettu muodossa. Mutta tällä ratkaisulla ei ole mitään tonicity, jos solukalvosta ei ole puolivälissä olevaa estettä.

Se voi palvella sinua: kalsiumnitraatti (CA (NO3) 2)

Liuennettuja suoloja on oltava vähän siten, että sen pitoisuus on pieni, kun taas veden "pitoisuus" on korkea. Solun ulkopuolella on enemmän vapaata vettä, toisin sanoen se ei ratkaise tai kosteutetaan liuennettua hiukkasia, sitä suurempi sen paine solukalvoon ja enemmän taipumus ylittää se laimentamaan solunsisäistä nestettä.

Hypotonisen liuoksen valmistelu

Näiden liuosten valmistelua varten samaa protokollaa noudatetaan kuin muihin ratkaisuihin. Sovellettavien aineiden massan asianmukaiset laskelmat tehdään. Sitten nämä punnitaan, liukenevat veteen ja ota lippu, joka on jaettu siihen, joka vastaa sitä.

Hypotonisella liuoksella on alhainen osmolaarisuus, yleensä alle 280 mOSM/L. Joten hypotonisen ratkaisun valmistettaessa meidän on laskettava osmolaarisuus siten, että sen arvo on alle 280 mOSM/L. Osmolaarisuus voidaan laskea seuraavalla yhtälöllä:

Osmolaarisuus = M · V · G

Missä m Se on liuenneen aineen molaarisuus ja v Hiukkasten lukumäärä, joissa yhdiste dissosioituu liuoksessa. Ei -elektrolyyttiset aineet eivät dissosioitu, joten V: n arvo on yhtä suuri kuin 1. Näin on glukoosi ja muut sokerit.

Sillä aikaa g on osmoottinen kerroin. Tämä on korjauskerroin sähköisesti varautuneiden hiukkasten (ionien) vuorovaikutukseen liuoksessa. Laimennettujen liuosten ja ei -dissosiaattisten aineiden, esimerkiksi glukoosin, arvon G -arvon arvo on 1. Sitten sanotaan, että molaari on identtinen sen osmolaarisuuden kanssa.

Esimerkki 1

Valmista natriumkloridiliuos (NaCl) 0,5 %: lla (P/tilavuus) tarkistamalla, onko se hypotoninen liuos vai ei. NaCl -molekyylipaino = 58,5 g/mol.

0,5 % gramma NaCl -liuos litraa kohti:

Voi palvella sinua: Kalsiumperoksidi (CAO2): Ominaisuudet, riskit ja käytöt

NaCl g/l = (0,5 g ÷ 100 ml) · 1.000 ml

= 5 g/l

Ja jatkamme sen molaarisuuden laskemista ja määritämme sen sitten osmolaarisuuden:

Molaarisuus = massa (g/l) ÷ molekyylipaino (g/mol)

= 5 g/l ÷ 58,5 g/mol

= 0,085 moolia/l

NaCl dissosioituu kahdessa hiukkasessa: Na⁺ (kationi) ja cl^- (anionia). Joten arvo V = 2. Lisäksi, koska se on laimennettu 0,5 %NaCl -liuos, voidaan olettaa, että G: n (osmoottinen kerroin) arvo on 1. Meillä on sitten:

Osmolaarisuus (NaCl) = molaarisuus · V · G

= 0,085 m · 2 · 1

= 0,170 OSM/L O 170 MOSM/L

Tämä on hypotoninen ratkaisu, koska sen osmolaarisuus on paljon alhaisempi kuin kehon nesteiden vertailusmolaarisuus, joka on plasman osmolaarisuus, jonka arvo on noin 300 mOSM/L L.

Esimerkki 2

Valmista kalsiumkloridin seoksen liuos (CACL₂) 0,055 % (P/V) ja glukoosi (C₆H₁₂JOMPIKUMPI₆) 4 % (P/V). Molekyylipainot: CACL₂ = 111 g/mol ja C₆H₁₂JOMPIKUMPI₆ = 180 g/mol.

Laskemme molaarisuuden, jolla on vastaavien liuenneiden aineiden pitoisuudet nopeudella 0,55 g/l ja 40 g/l:

Molaarisuus (CACl₂) = 0,55 g/l ÷ 111 g/mol

= 4,95 · 10^-3 M

= 4,95 mm

Molaarisuus (c₆H₁₂JOMPIKUMPI₆) = 40 g/l ÷ 180 g/mol

= 0,222 m

= 222 mm

Ja samalla tavalla kuin laskemme osmolaarisuudet tietäen, että napsautus₂ Se dissosioituu kolmeen ioniin, kaksi Cl: tä^- Ja ca²⁺, ja olettaen, että ne ovat hyvin laimennettuja ratkaisuja, joten arvo v Se on 1. Meillä on:

Osmolaarisuus (CACL₂) = 4,95 mm · 3 · 1

= 14,85 MOSM/L

Osmolaarisuus (c₆H₁₂JOMPIKUMPI₆) = 222 mm · 1 · 1

= 222 MOSM/L

Lopuksi, liuoksen kokonaisosmolaarisuudesta tulee yksittäisten osmolaarisuuksien summa; toisin sanoen NaCl: n ja glukoosin joukosta. Tämä on siis:

Voi palvella sinua: tulenkestävä materiaali

Liuoksen kokonaismäärä = cacl osmolaarisuus₂ + osmolaarisuus C₆H₁₂JOMPIKUMPI₆

= 222 MOSM/L + 14,85 MOSM/L

= 236,85 MOSM/L

Kalsiumin ja glukoosikloridin seoksen liu.

Esimerkkejä hypotonisista ratkaisuista

Natriumkloridiliuos

0,45 % natriumkloridiliuosta annetaan laskimonsisäisesti diabeettisen ketoosipotilaille, joilla on kuivuminen interstitiaalisissa ja solunsisäisissä osastoissa. Vesi virtaa plasmasta näihin osastoihin.

Ringer -laktaattiliuos

Ringer -laktaattiliuos nro 19 on toinen esimerkki hypotonisesta ratkaisusta. Sen koostumus on 0,6 g natriumkloridia, 0,03 g kaliumkloridia, 0,02 g kalsiumkloridia, 0,31 g natriumlaktaattia ja 100 ml tislattua vettä. Se on ratkaisu, jota käytetään potilaan nesteytykseen ja on hiukan hypotoninen (274 mOSm/l).

Viitteet

1. Lehr Spilvasta,. Ja muktanit, ja. (1999). Opas farmaseuttisiin erikoisuuksiin Venezuelassa. Xxxvª -painos. Globaalit versiot.
2. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
3. Wikipedia. (2020). Toniikka. Haettu: vuonna.Wikipedia.org
4. Union Media LLC. (2020). Isotoninen, hypotoninen ja hypertoninen ratkaisu. Haettu osoitteesta: UnionTestPrep.com
5. Lodish H, Berk A, Zipursky SL, et ai. (2000). Kohta 15.8Smoosi, vesikanavat ja solutilavuuden säätely. NCBI -kirjahylly. Palautettu: NCBI.Nlm.NIH.Hallitus
6. John Brennan. (13. maaliskuuta 2018). Kuinka laskea isotonisuus. Toipunut: tiedekunnasta.com