Yhdistetty peräkkäin

Peräkkäisyys koostuu keltaisista ja sinisistä neliöistä. Lähde: f. Zapata

Mikä on komposiittinen peräkkäin?

Eräs yhdistetty peräkkäin Se koostuu elementtien sekvenssistä, joka on luotu kahdesta (tai useammasta) erilaisesta ja vaihtoehtoisesta peräkkäisestä. Jokaisella näistä peräkkäisistä on erityinen sääntö, jota käytetään niiden elementtien löytämiseen.

Elementtien ei tarvitse olla numeerisia, jotta ne voivat olla luvuja, symboleja tai kirjaimia, mutta niitä, jotka perustuvat numeroihin, kutsutaan aritmeettiset peräkkäit. Kuva, jolla artikkeli alkaa.

Tässä peräkkäin se alkaa suuresta neliöstä, joka koostuu 8 keltaisesta neliöstä ja sinisestä neliöstä. Seuraavan termin saamiseksi keltainen neliö lisätään ensimmäisen ja kolmannen neliörivin vasemmalle tai oikealle. Keskusrivin tila on täynnä sinistä neliötä.

Jokaista sekvenssin kuvaa kutsutaan termi. Jos haluat löytää viidennen termin, sinun on lisättävä keltainen neliö ensimmäisen ja kolmannen rivin oikealla puolella ja sininen neliö toisessa rivissä:

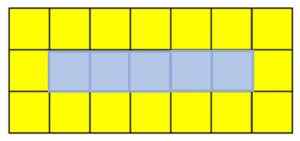Viides termi keltaisten ja sinisten neliöiden peräkkäin. Lähde: f. Zapata

Selitys

Yhdistetyissä peräkkäisissä termit saadaan vuorotellen kahden tai useamman riippumattoman yksinkertaisen peräkkäin ehdot. Idean ymmärtämiseksi paremmin sitä tulisi tarkistaa yksinkertaisen peräkkäisen yksityiskohdat.

Esimerkiksi seuraava yksinkertainen peräkkäisyys koostuu luonnollisista numeroista:

2, 4, 6, 8, 10, 12 ..

Suspensat osoittavat, että peräkkäin on ääretön termi.

Jokainen termi on merkitty pienellä kirjaimella ja numerolla. Tämä luku osoittaa sijainnin tai indeksi jokaisen ajanjakson. Edellisessä peräkkäisissä vaiheissa voit kirjoittaa:

-lla₁ = 2; -lla₂ = 4; -lla₃ = 6; -lla₄ = 8 ..

On erittäin kätevää olla tapa laskea kaikki peräkkäin toivotut termit, toisin sanoen sen erityinen sääntö. Hänen kanssaan N-ésimo-termi, jompikumpi Yleinen termi, merkitty nimellä a_n.

Voi palvella sinua: tasa -arvon ominaisuudet

Jatkamalla esimerkkiä parillisten numeroiden peräkkäisestä, voit määrittää tavan laskea termi n-ésimo edellisestä termistä:

-lla_n = a_N-1 + 2

Minne_N-1 Se on termi, joka edeltää_n.

Tietenkin olisi parempi tietää yleinen termi riippumatta muista termeistä. Tässä peräkkäin on helppo huomata, että mikä tahansa termi kertoo 2: lla sen sijainnilla, kun otetaan huomioon termin alaosa. Tällä tavalla se on kirjoitettu:

-lla_n = 2n

Muinaiset kreikkalaiset tiesivät jo tasaisen ja parittoman lukumäärän peräkkäiset. Sillä välin parittomien luonnollisten lukujen peräkkäisyys voidaan kirjoittaa seuraavasti:

1, 3, 5, 7, 9, 11 ..

Ja yhdistämällä parillisen numeron peräkkäin parittoman kanssa, seuraava yhdisteiden peräkkäisyys on:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Jonka tulos on luonnollisten lukujen joukko.

Yhdisteen peräkkäisyyden termit

Voi olla hauskaa yrittää löytää suhde, joka esiintyy numerosarjassa, jolle se on tarkkailtava huolellisesti ja yritettävä tunnistaa, onko se yhdistelmä peräkkäin.

Kahdesta peräkkäisestä peräkkäisen yleinen muoto on:

-lla₁, b -₁, -lla₂, b -₂, -lla₃, b -₃, -lla₄, b -₄,..

Minne₁, -lla₂, -lla₃, -lla₄,... ovat ensimmäisen peräkkäisen ja b: n ehdot₁, b -₂, b -₃, b -₄,… Toisen toisen. Ne ovat aina välissä, kuten tässä esimerkissä:

7, 8, 14, 16, kaksikymmentäyksi, 24, 28, 32, 35..

Mikä on seuraava termi?

Tiedäksesi, tiedä seuraaja kahdessa vaihtoehtoisessa numerosarjassa seuraavasti:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

Ensimmäisessä näistä sarjoista seitsemän kerros ilmestyy:

-lla₁ = 7 × 1 = 7; -lla₂ = 7 × 2 = 14; -lla₃ = 7 × 3 = 21; -lla₄ = 7 × 4 = 28; -lla₅ = 7 × 5 = 35

Tämän peräkkäisyyden yleinen termi on:

-lla_n = 7n

Ja toisessa se on 8: 8:

b -₁ = 8 × 1 = 8; b -₂ = 8 × 2 = 16; b -₃ = 8 × 3 = 24; b -₄ = 8 × 4 = 32

Joten sen yleinen termi on:

Se voi palvella sinua: todellinen todellisen muuttujan toiminto ja sen graafinen esitys

b -_n = 8n

Palattuaan alkuperäiseen yhdistelmän peräkkäisyyteen, 35 kuuluu ensimmäiseen sekvenssiin, jonka termit ovat₁, -lla₂, -lla₃, -lla₄ … 35 on viides termi, joten seuraavan termin on oltava B₅, joka saadaan helposti säännöstä yleisen termin löytämiseksi:

b -₅ = 8 × 5 = 40

Ja se on kirjoitettu:

7, 8, 14, 16, kaksikymmentäyksi, 24, 28, 32, 35, 40 ..

Esimerkkejä yhdistelmäkeskuksista

Esimerkki 1

Voit luoda komposiitti -peräkkäisyyden geometrisillä hahmoilla, kuten neliöllä ja ympyrällä, järjestämällä ne alla esitetyllä tavalla:

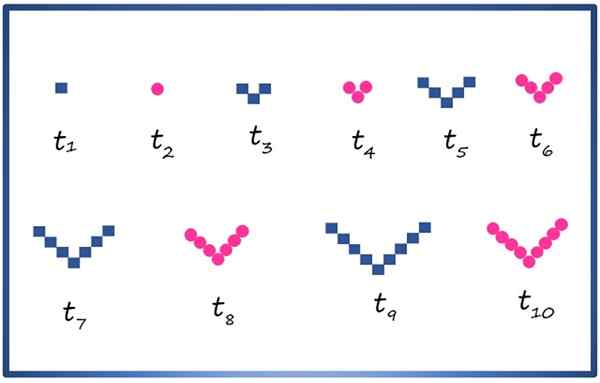Komposiittisen peräkkäisen ensimmäisen 10 ensimmäisen termin kanssa neliön geometristen elementtien ja ympyrän kanssa. Lähde: f. Zapata

Jokainen termi on merkitty T: llä₁, t₂, t₃, t₄ …, Parque -indeksin termit koostuvat ympyröistä ja parittoman indeksin, neliöistä. Sekvenssin huolellisesti tarkkailemalla on mahdollista tietää esimerkiksi, että termi t_yksitoista, Se ei näy kuvassa, koostuu 11 neliöstä, joissa on V -.

Esimerkki 2

Seuraava yhdistelmä peräkkäisyys koostuu symboleista, tässä tapauksessa kirjaimet r ja s:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSS ..

Jokainen uusi termi on rakennettu lisäämällä kirje edelliseen. Esitetyn sekvenssin neljä ensimmäistä termiä ovat:

t₁= R - ; t₂= HH ; t₃= RR ; t₄= SSS ..

Ja seuraava termi, joka ilmestyy esitetyn ehtojen jälkeen, on:

t_yksitoista= Rrrrrr

Esimerkki 3

Aikaisemmat esimerkit osoittivat nousevia peräkkäisiä, joissa kukin arvo kasvaa jollain tavalla edellisen suhteen. Mutta sen ei aina tarvitse olla tällä tavalla, koska peräkkäiset voivat olla laskeutuvia, ts. Niillä on väheneminen malli.

Ja nousevat peräkkäit voidaan yhdistää laskeviin peräkkäin.

Seuraava numeerinen peräkkäisyys koostuu:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Se voidaan erottaa kahteen peräkkäin:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Mitkä ovat arvot, jotka on sijoitettava tyhjiin tiloihin?

Tarkkailemalla ensimmäistä peräkkäistä huolellisesti, jokainen termi saadaan lisäämällä 3 edelliseen termiin. Siksi se on nouseva peräkkäin:

Voi palvella sinua: Kulma siirtymä

7 = 4 + 3

10 = 7 + 3

Siksi ensimmäisessä tyhjässä tilassa sinun on sijoitettava:

10 + 3 = 13

Tämän jälkeen seuraava termi on käytännössä:

16 = 13 + 3

Ja toisessa tyhjässä menee:

16 + 3 = 19

Toinen peräkkäisyys on laskeva ja puuttuvien termien löytäminen on erittäin helppoa, koska havaitaan, että jokainen termi saadaan vähentämällä 1 edellisestä termistä, siksi:

36, 35, 3. 4, 33, 32..

Lopuksi voit kirjoittaa:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Ratkaisut

Harjoitus 1

Edellisen osan esimerkistä 3 koostuu:

a) kuuluu 29 mainitulle peräkkäisyydelle?

b) Kirjoita vielä 10 termiä tästä peräkkäisestä

Vastaa

Kyllä, se kuuluu, koska toinen peräkkäisyys on laskeva ja sen termit saadaan vähentämällä 1 edellisestä termistä. Tällä tavalla se lopulta saavuttaa 29.

Vastaus b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Huomaa, että jotkut termit toistetaan.

Harjoitus 2

Löydä puuttuvat termit seuraavasta yhdisteestä peräkkäin:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Vastaus

Odd -termit on kirjoitettu ensimmäisen peräkkäisen saamiseksi:

100, 115, 130, 145, 160, ..

Havaitaan, että jokaisen termin löytämiseksi sinun on lisättävä 15 edelliseen termiin, joten 160 -vuotiaana oleva termi on 175.

Toinen peräkkäinen koostuu:

500, 480, 460, 440, 420, ..

Jokainen termi eroaa edellisestä 20: sta, peräkkäisyys on laskeva, joten termi 420 on 400.

Näiden tietojen avulla alkuperäiseen yhdisteeseen peräkkäin lisätään vielä kaksi termiä, kuten tämä:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Viitteet

1. Larson, r. (2012). Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
2. Stewart, J. (2007). Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
3. Yhdistelmäkeskukset. Toipunut: Media.EducacionCampeche.Hölynpöly.MX.
4. Numeeriset peräkkäit. Haettu: Matemathweb.com.
5. Peräkkäit. Aritmeettinen ja geometrinen eteneminen. Haettu: Macmillaneducation.On.